There’s a line in machine studying particularly within the concept behind Assist Vector Machines (SVMs), that’s each breathtaking and tormenting:
“A posh pattern-classification downside, forged in a high-dimensional house nonlinearly, is extra prone to be linearly separable than in a low-dimensional house.” — Cowl’s Theorem
The primary time I learn this, I used to be surprised. It felt like magic. You imply to say — simply by lifting knowledge right into a higher-dimensional house, we are able to make the unattainable potential? That’s lovely. But in addition… why?
This concept haunted me. I understood the assertion, however I couldn’t internalize why it labored.
Someplace alongside the best way, I stumbled upon this analogy:
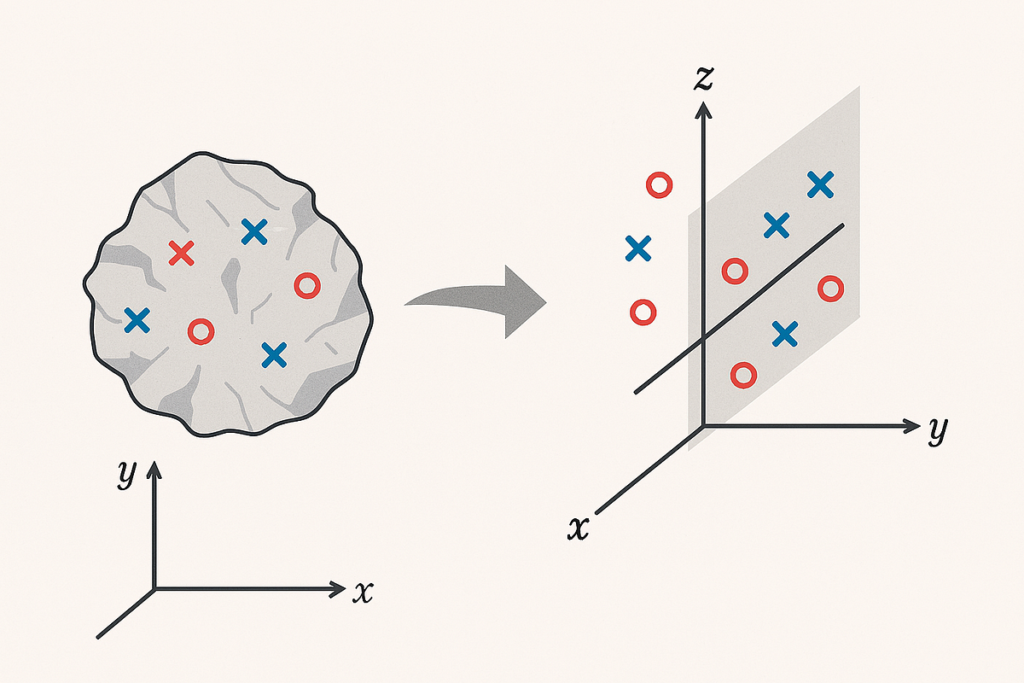
Think about a crumpled piece of paper with pink and blue dots scattered throughout it. In its crumpled state, the dots are jumbled — no straight line can separate them. However in case you uncrumple the paper, instantly the pink and blue dots fall into place. A easy line now does the job.
- The crumpled paper represents the low-dimensional house. The info factors (dots) are shut to one another in a non-linear method, making them inseparable by a straight line.
- The flat paper represents the high-dimensional house. By including a brand new dimension (just like the “peak” of the paper as you uncrumple it), you’re stretching the info out in a method that separates the beforehand intertwined factors.
I liked this analogy. It was vivid, intuitive, and stylish. However I additionally hated it. As a result of it didn’t inform me how or why the uncrumpling works. What does it imply to stretch an area? What does it imply to elevate knowledge? The place does the separability come from?
To discover a actual reply, I needed to dig right into a traditional downside that refuses to be linear: the XOR gate.
The traditional XOR linear separability downside. 4 factors:
Plotted in 2D, the constructive class sits on reverse corners. No line can separate them.
There’s a transformation: “z=x⋅y”. The core thought was lifting the factors in 3D. However in some way I couldn’t visualize this and I gave it up.
Then there was one thing else, primarily based on the identical thought.
z=(x−y)².
All of a sudden, the whole lot clicked.
Now the XOR-positive instances have z=1, and the negatives have z=0. A easy threshold — say, z>0.5— cleanly separates the courses.
This wasn’t only a trick. It was a revelation.
The transformation works as a result of the nonlinear characteristic z captures the important distinction that XOR exploits.
The XOR perform is essentially about inequality:
XOR(x,y) = 1 iff x≠y
This implies the perform doesn’t care in regards to the particular person values of x or y — solely whether or not they differ. The linear mannequin fails as a result of it can not mannequin the interplay x≠y with out further options.
The geometry of the enter house hid the logic of the perform. The transformation z = (x — y)² uncovered it.
Right here’s the instinct. In lower-dimensional areas (say 2D), the distinction between factors from completely different courses is usually entangled — hidden in ways in which defy linear separation. However by introducing a brand new dimension that captures the latent distinction, we are able to reveal what was beforehand invisible. The proper transformation untangles the geometry and makes the separation clear.
Or extra formally:
In low-dimensional areas, the discriminative construction between courses could also be entangled or obscured — making linear separation unattainable. By introducing a rigorously constructed nonlinear characteristic that captures the latent distinction (e.g., interplay, symmetry, or inequality), we successfully elevate the info right into a higher-dimensional house the place the courses grow to be linearly separable. The success of this strategy hinges on whether or not the added dimension encodes a class-relevant transformation, not simply arbitrary variation.
Cowl’s theorem isn’t nearly including dimensions. It’s about including the proper dimensions — ones that encode latent construction. The explanation high-dimensional nonlinear mappings work is as a result of they enhance the possibility that some axis will align with the category boundary.
However whenever you discover the proper transformation — like (x — y)² for XOR — you don’t want luck. You get readability.
The stretching analogy now is smart. You’re not simply uncrumpling paper — you’re reorienting the house to reveal distinction. You’re turning tangled geometry into clear logic.
Cowl’s theorem as soon as felt like a good looking thriller. Now it appears like a problem:
Can you discover the transformation that reveals the reality?
Typically, that transformation is buried in algebra. Typically, it’s hidden in area data. However whenever you discover it, the world turns into linear once more.
And that, to me, is the actual magic.