That is the second time in latest months {that a} small mannequin carried out equally properly (or higher) than the billion-parameter massive fashions. Granted math issues are distinctive: largely quantifiable and verifiable.
“In contrast to options counting on superior LLMs for information synthesis, rStar-Math leverages smaller language fashions (SLMs) with Monte Carlo Tree Search (MCTS) to determine a self-evolutionary course of, iteratively producing higher-quality coaching information.”
End result: “4 rounds of self-evolution with tens of millions of synthesized options for 747k math issues … it improves Qwen2.5-Math-7B from 58.8% to 90.0% and Phi3-mini-3.8B from 41.4% to 86.4%, surpassing o1-preview by +4.5% and +0.9%.”
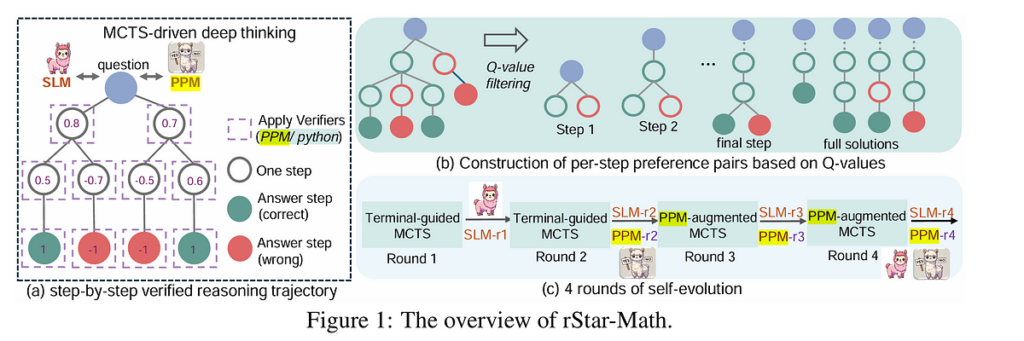
Course of reward modeling (PRM) supplies fine-grained suggestions on intermediate steps as a result of incorrect intermediate steps considerably lower information high quality in math.
SLM samples candidate nodes, every producing a one-step CoT and the corresponding Python code. Solely nodes with profitable Python code execution are retained, mitigating errors in intermediate steps. MCTS routinely assign (self-annotate) a Q-value to every intermediate step primarily based on its contribution: steps contributing to extra trajectories that result in the proper reply are given larger Q-values and thought of larger high quality.
SLM as a course of choice mannequin (PPM) to foretell reward labels for every math reasoning step. Though Q-values aren’t exact, they will reliably distinguish constructive (right) steps from unfavorable (irrelevant/incorrect) ones. Utilizing choice pairs and pairwise rating loss, as an alternative of instantly utilizing Q-values as reward labels, eradicate the inherently noise and imprecision in stepwise reward task.
Paper on arXiv: https://arxiv.org/abs/2501.04519