On this article i’ll be sharing an understanding and mathematical facet of Kernel Strategies just about Stanford College’s CS229 course taught by the famend British-American pc scientist Dr.Andrew Ng and Dr. Tengyu Ma.
Function maps
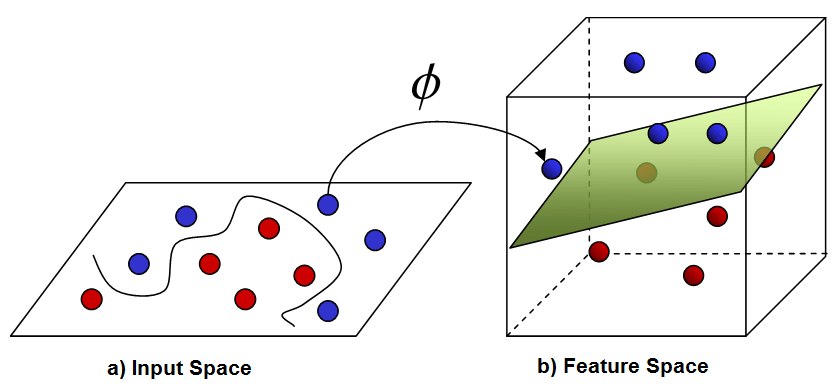
Typically, a easy linear perform could not give correct outcomes for an issue. For instance, if we’re predicting home costs, a straight-line relationship (linear perform) won’t seize the sample properly. non-linear perform would possibly match the information higher and provides extra correct predictions.
Think about a cubic equation:
We are able to rewrite this perform utilizing a function map ϕ : R→R⁴ which maps a single-dimensional actual quantity R right into a four-dimensional vector R⁴ :
Let θ ∈ R⁴ be the vector containing θ0,θ1,θ2,θ3 as entries. Then we are able to
rewrite the cubic perform in x as:
In such circumstances, we want fashions that may deal with extra complicated relationships. Kernel strategies assist by remodeling the information right into a higher-dimensional area utilizing a kernel perform, making it simpler for the mannequin to seek out patterns and make higher predictions.
LMS (least imply squares) with options
In fundamental linear regression, the mannequin is represented by θ^T x , the place x represents the enter options and θ is the vector of parameters to be discovered. Nonetheless, when a easy linear mannequin just isn’t ample to seize the connection, we remodel the enter information utilizing a function map ϕ(x) , which maps the enter x right into a higher-dimensional area. The purpose is then to suit the mannequin θ^T *ϕ(x) , the place θ is a vector of parameters within the higher-dimensional area, making it extra able to capturing complicated relationships. For odd least squares, the batch gradient descent replace is:
Equally stochastic gradient descent replace rule is:
LMS with the Kernel Trick
When coping with high-dimensional function mappings, direct computation turns into costly, particularly when the function map entails high-degree polynomials. To beat this, we are able to use a kernel trick that avoids explicitly computing the function map. As a substitute, we use a kernel perform Ok(x, z) , which computes the inside product
within the higher-dimensional area. This enables for extra environment friendly computation, because the kernel perform will be precomputed and doesn’t require the specific computation of ϕ(x) . The replace rule for the parameters θ will be expressed as a linear mixture of the function vectors, and we symbolize θ iteratively with coefficients β. The replace rule for β depends upon the kernel values, and the kernel perform captures the required info from the function map. This ends in an environment friendly gradient descent algorithm that avoids explicitly working with high-dimensional function vectors, enhancing each time and area complexity. The ultimate prediction will be computed utilizing the kernel values, while not having the specific type of ϕ(x) .
The gradient descent replace rule will be expressed as a linear mixture of the function vectors, represented as
At every iteration, the replace for the coefficients βi is given by:
The kernel trick permits us to carry out operations within the higher-dimensional area with out explicitly computing ϕ(x) , making the method extra computationally environment friendly. Lastly, the prediction will be computed as:
Legitimate Kernels and the Mercer Theorem
Mercer’s Theorem states that for a perform Ok(x, z) to be a legitimate kernel, it should correspond to an inside product in a higher-dimensional function area. Legitimate kernels should fulfill two situations: symmetry (i.e., Ok(x, z) = Ok(z, x) ) and constructive semi-definiteness (guaranteeing the Gram matrix is non-negative). Some common kernels embrace: