Neural Networks – Intuitively and Exhaustively Explained

On this article we’ll type an intensive understanding of the neural community, a cornerstone know-how underpinning just about all leading edge AI techniques. We’ll first discover neurons within the human mind, after which discover how they shaped the basic inspiration for neural networks in AI. We’ll then discover back-propagation, the algorithm used to coach neural networks to do cool stuff. Lastly, after forging an intensive conceptual understanding, we’ll implement a Neural Community ourselves from scratch and prepare it to unravel a toy downside.

---

Who’s this convenient for? Anybody who desires to type an entire understanding of the state-of-the-art of AI.

How superior is that this put up? This text is designed to be accessible to newbies, and in addition comprises thorough data which can function a helpful refresher for extra skilled readers.

Pre-requisites: None

---

Inspiration From the Mind

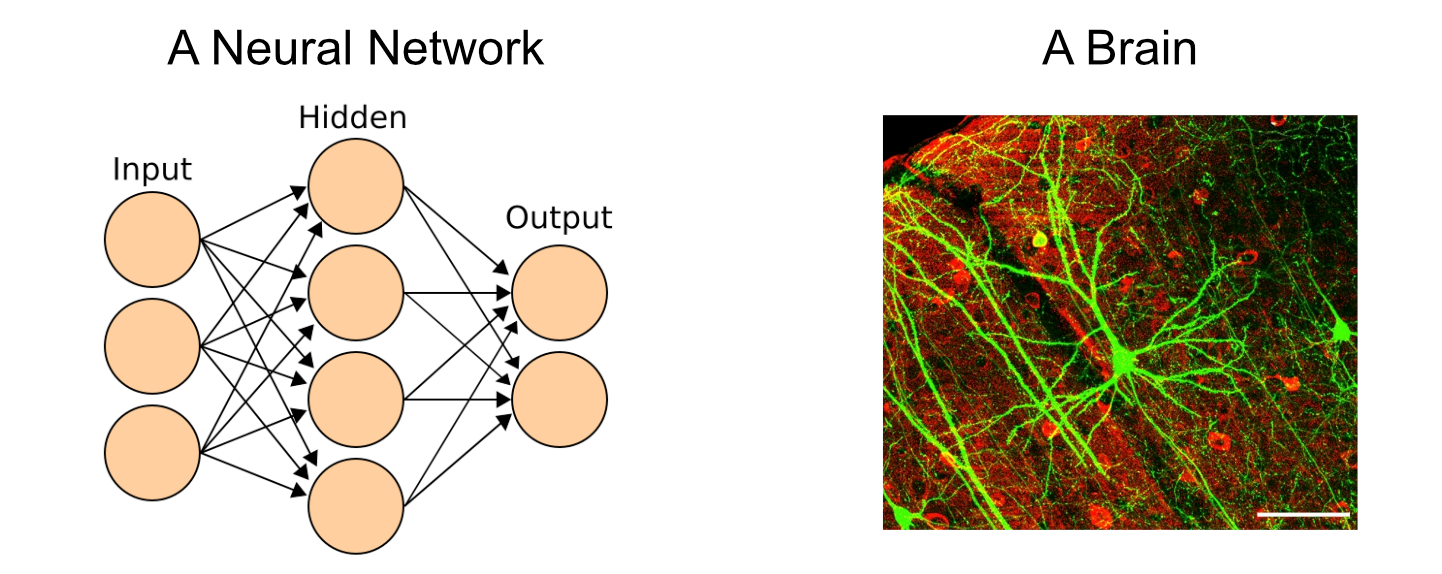
Neural networks take direct inspiration from the human mind, which is made up of billions of extremely complicated cells known as neurons.

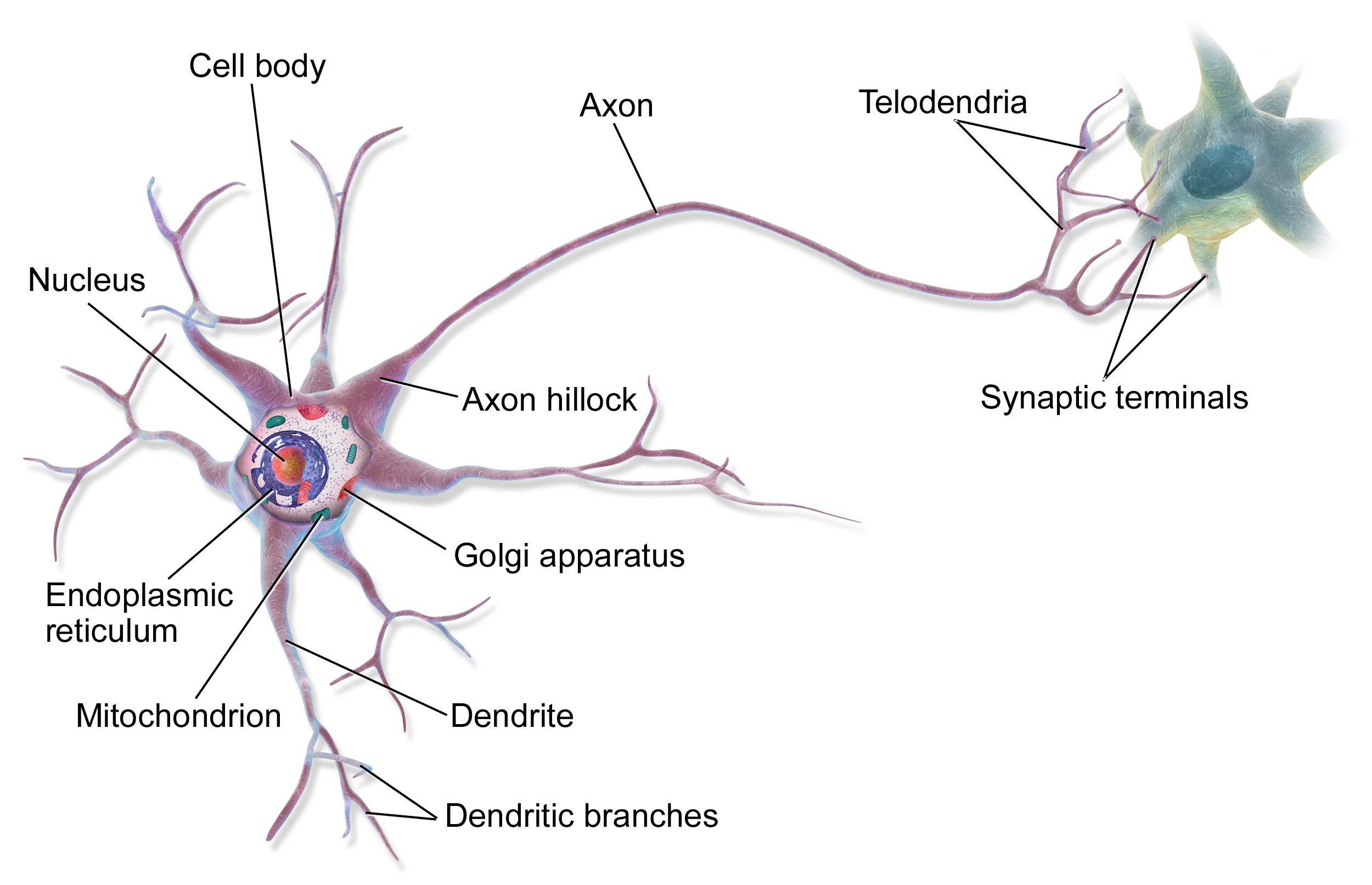
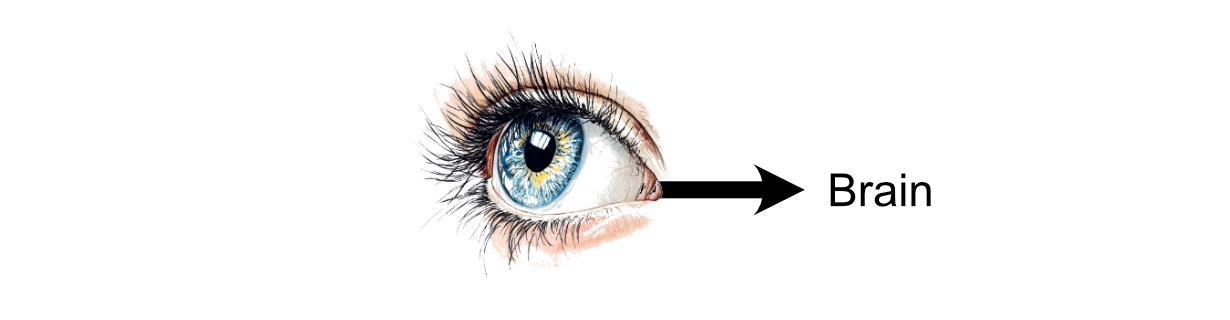
The method of considering throughout the human mind is the results of communication between neurons. You would possibly obtain stimulus within the type of one thing you noticed, then that data is propagated to neurons within the mind through electrochemical alerts.

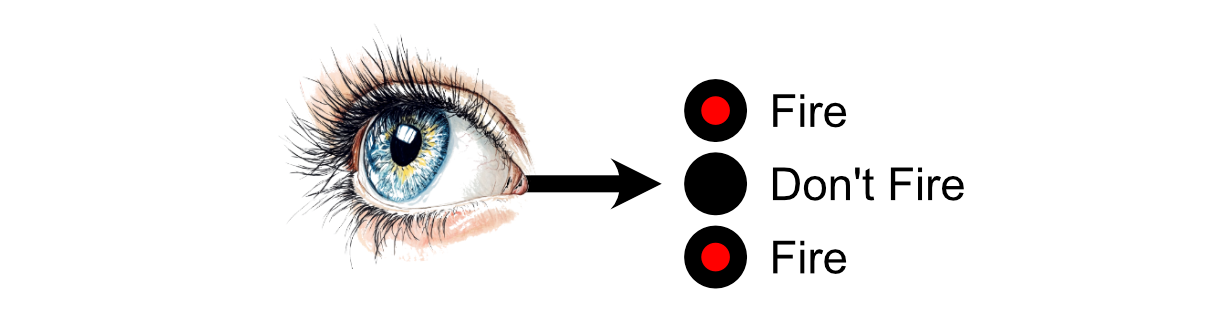
The primary neurons within the mind obtain that stimulus, then every neuron could select whether or not or to not “fireplace” primarily based on how a lot stimulus it obtained. “Firing”, on this case, is a neurons choice to ship alerts to the neurons it’s linked to.

Then the neurons which these Neurons are linked to could or could not select to fireplace.

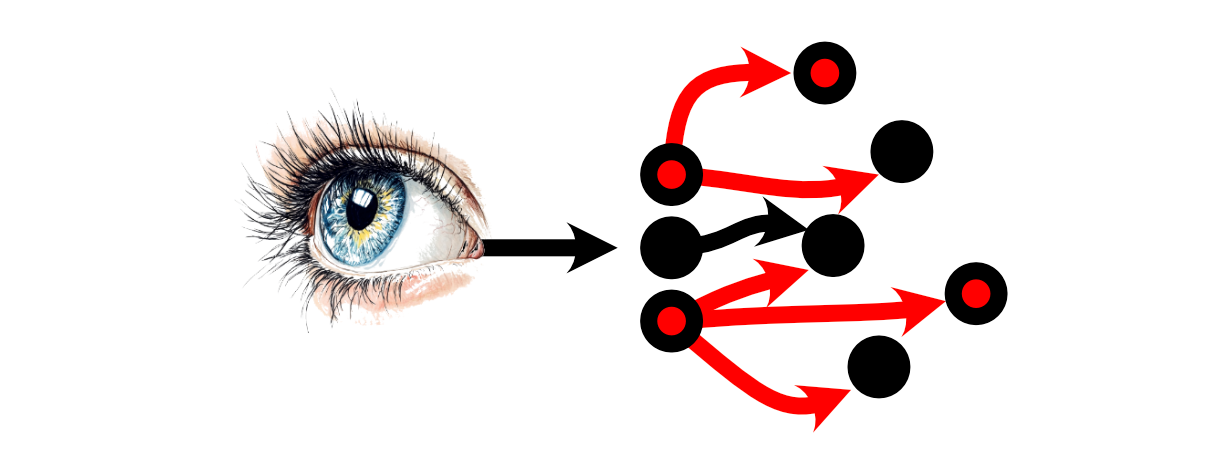
Thus, a “thought” may be conceptualized as a lot of neurons selecting to, or to not fireplace primarily based on the stimulus from different neurons.

As one navigates all through the world, one might need sure ideas greater than one other particular person. A cellist would possibly use some neurons greater than a mathematician, for example.

After we use sure neurons extra steadily, their connections turn out to be stronger, growing the depth of these connections. After we don’t use sure neurons, these connections weaken. This normal rule has impressed the phrase “Neurons that fireside collectively, wire collectively”, and is the high-level high quality of the mind which is answerable for the educational course of.

I’m not a neurologist, so after all this can be a tremendously simplified description of the mind. Nonetheless, it’s sufficient to know the basic thought of a neural community.

The Instinct of Neural Networks

Neural networks are, basically, a mathematically handy and simplified model of neurons throughout the mind. A neural community is made up of parts known as “perceptrons”, that are straight impressed by neurons.

Perceptrons absorb information, like a neuron does,

mixture that information, like a neuron does,

then output a sign primarily based on the enter, like a neuron does.

A neural community may be conceptualized as a giant community of those perceptrons, similar to the mind is a giant community of neurons.

When a neuron within the mind fires, it does in order a binary choice. Or, in different phrases, neurons both fireplace or they don’t. Perceptrons, then again, don’t “fireplace” per-se, however output a variety of numbers primarily based on the perceptrons enter.

Neurons throughout the mind can get away with their comparatively easy binary inputs and outputs as a result of ideas exist over time. Neurons basically pulse at different rates, with slower and quicker pulses speaking totally different data.

So, neurons have easy inputs and outputs within the type of on or off pulses, however the charge at which they pulse can talk complicated data. Perceptrons solely see an enter as soon as per cross by the community, however their enter and output generally is a steady vary of values. In the event you’re conversant in electronics, you would possibly replicate on how that is just like the connection between digital and analogue alerts.

The best way the maths for a perceptron truly shakes out is fairly easy. A typical neural community consists of a bunch of weights connecting the perceptron’s of various layers collectively.

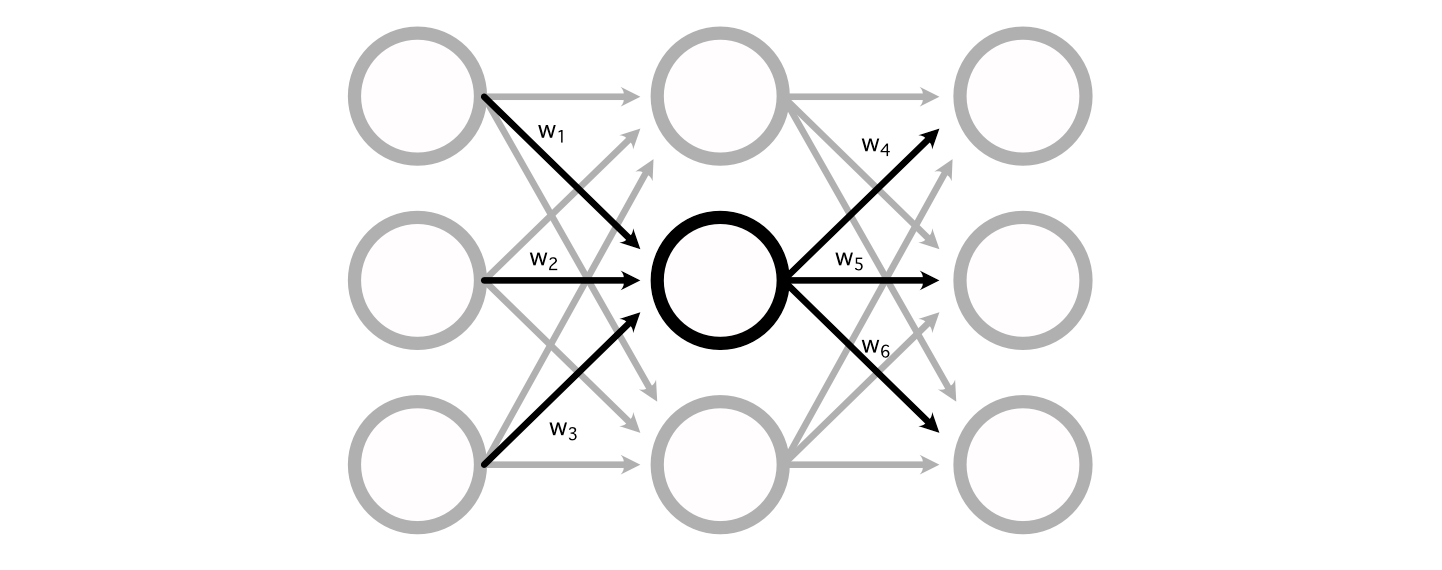
You may calculate the worth of a specific perceptron by including up all of the inputs, multiplied by their respective weights.

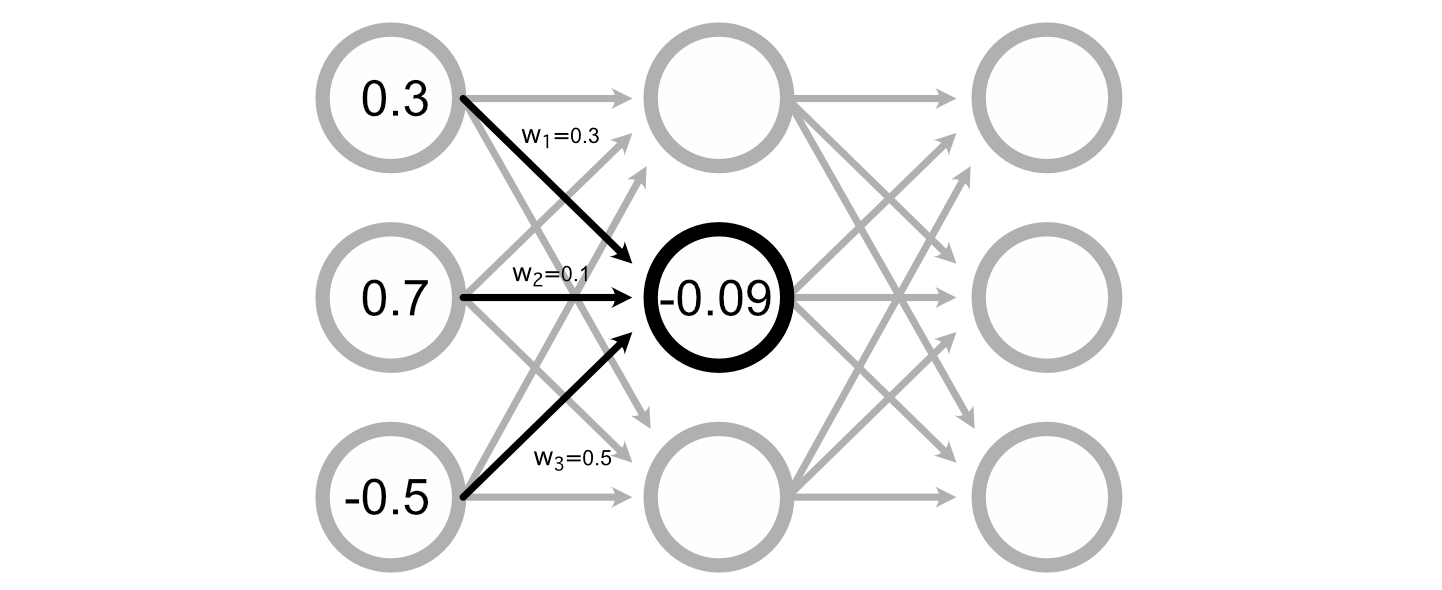
Many Neural Networks even have a “bias” related to every perceptron, which is added to the sum of the inputs to calculate the perceptron’s worth.

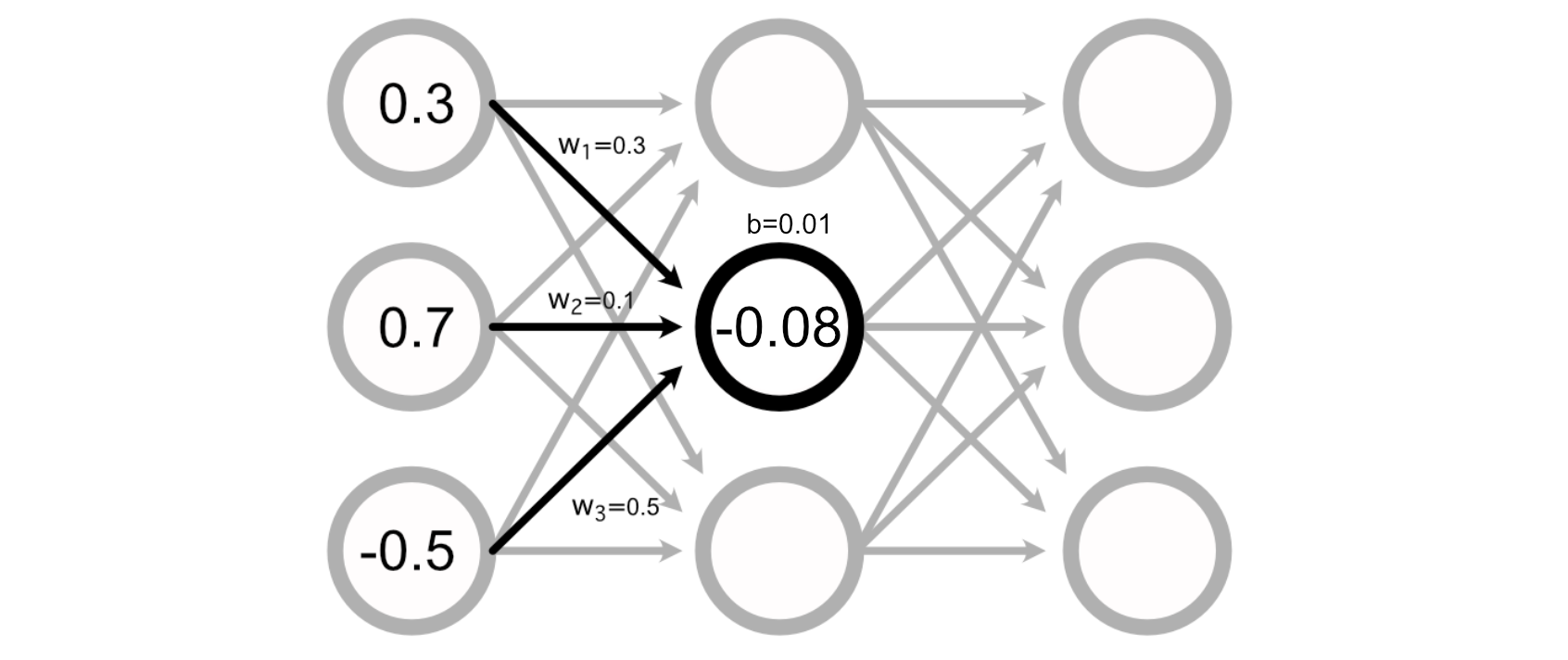
Calculating the output of a neural community, then, is simply doing a bunch of addition and multiplication to calculate the worth of all of the perceptrons.

Typically information scientists discuss with this normal operation as a “linear projection”, as a result of we’re mapping an enter into an output through linear operations (addition and multiplication). One downside with this method is, even should you daisy chain a billion of those layers collectively, the ensuing mannequin will nonetheless simply be a linear relationship between the enter and output as a result of it’s all simply addition and multiplication.

It is a major problem as a result of not all relationships between an enter and output are linear. To get round this, information scientists make use of one thing known as an “activation perform”. These are non-linear capabilities which may be injected all through the mannequin to, basically, sprinkle in some non-linearity.

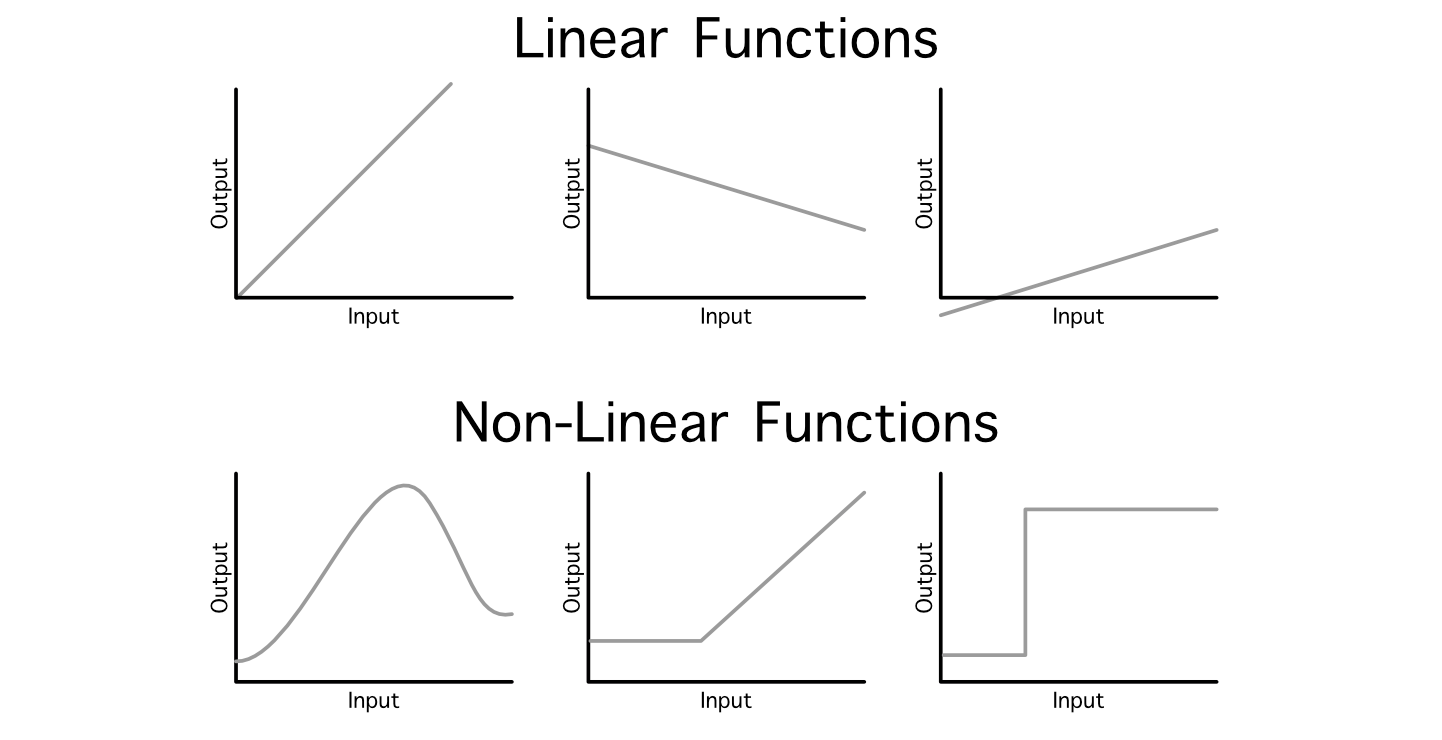
by interweaving non-linear activation capabilities between linear projections, neural networks are able to studying very complicated capabilities,

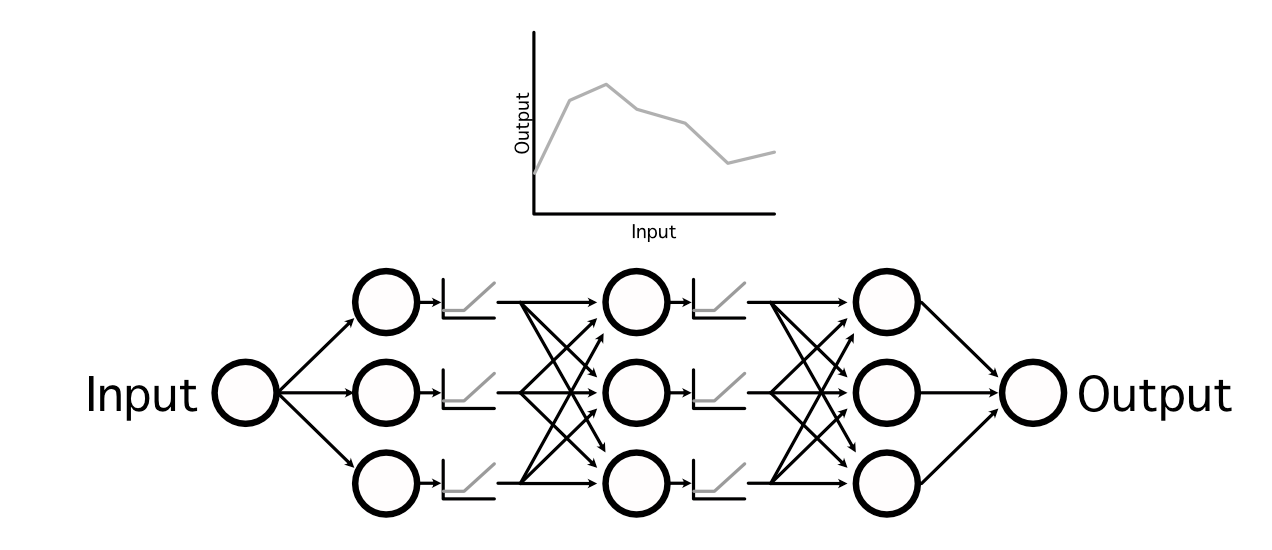
In AI there are a lot of common activation capabilities, however the business has largely converged on three common ones: ReLU, Sigmoid, and Softmax, that are utilized in quite a lot of totally different functions. Out of all of them, ReLU is the commonest as a consequence of its simplicity and talent to generalize to imitate virtually some other perform.

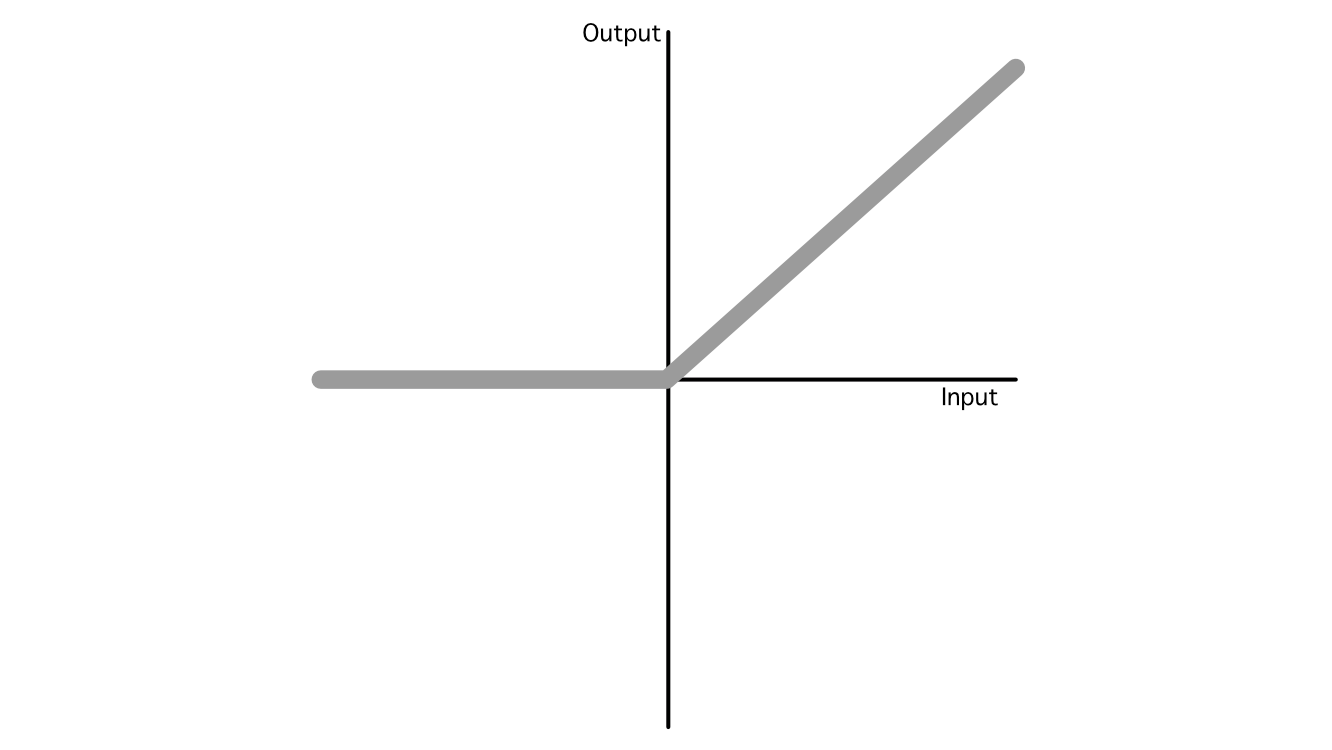
So, that’s the essence of how AI fashions make predictions. It’s a bunch of addition and multiplication with some nonlinear capabilities sprinkled in between.

One other defining attribute of neural networks is that they are often educated to be higher at fixing a sure downside, which we’ll discover within the subsequent part.

Again Propagation

One of many basic concepts of AI is which you could “prepare” a mannequin. That is finished by asking a neural community (which begins its life as a giant pile of random information) to do some process. Then, you by some means replace the mannequin primarily based on how the mannequin’s output compares to a identified good reply.

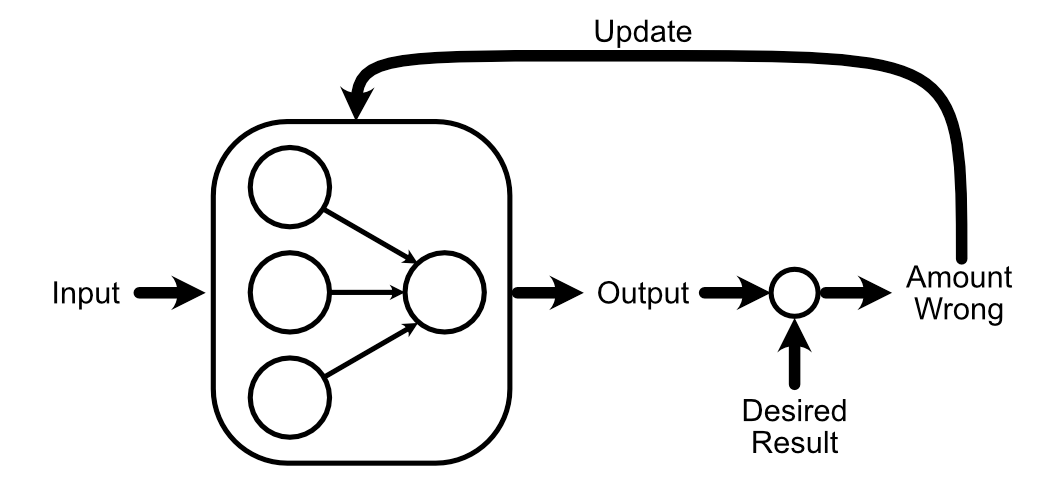
For this part, let’s think about a neural community with an enter layer, a hidden layer, and an output layer.

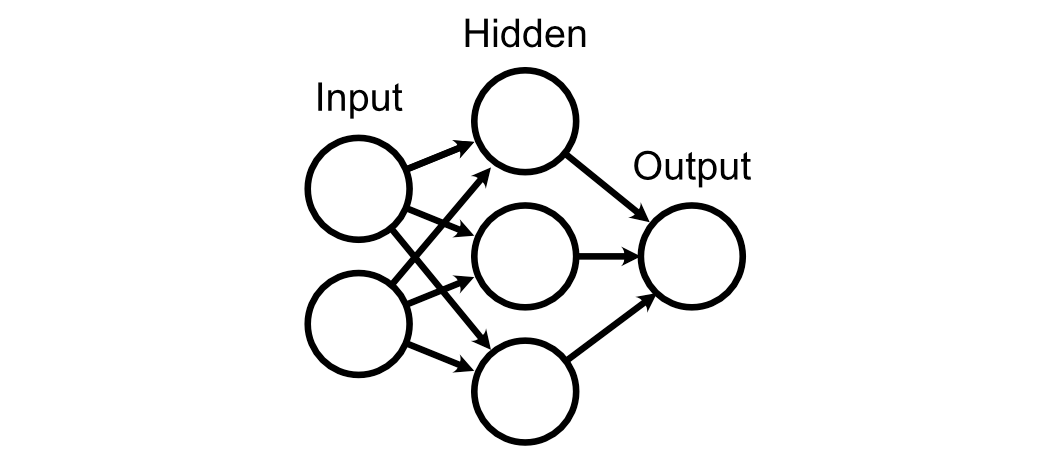
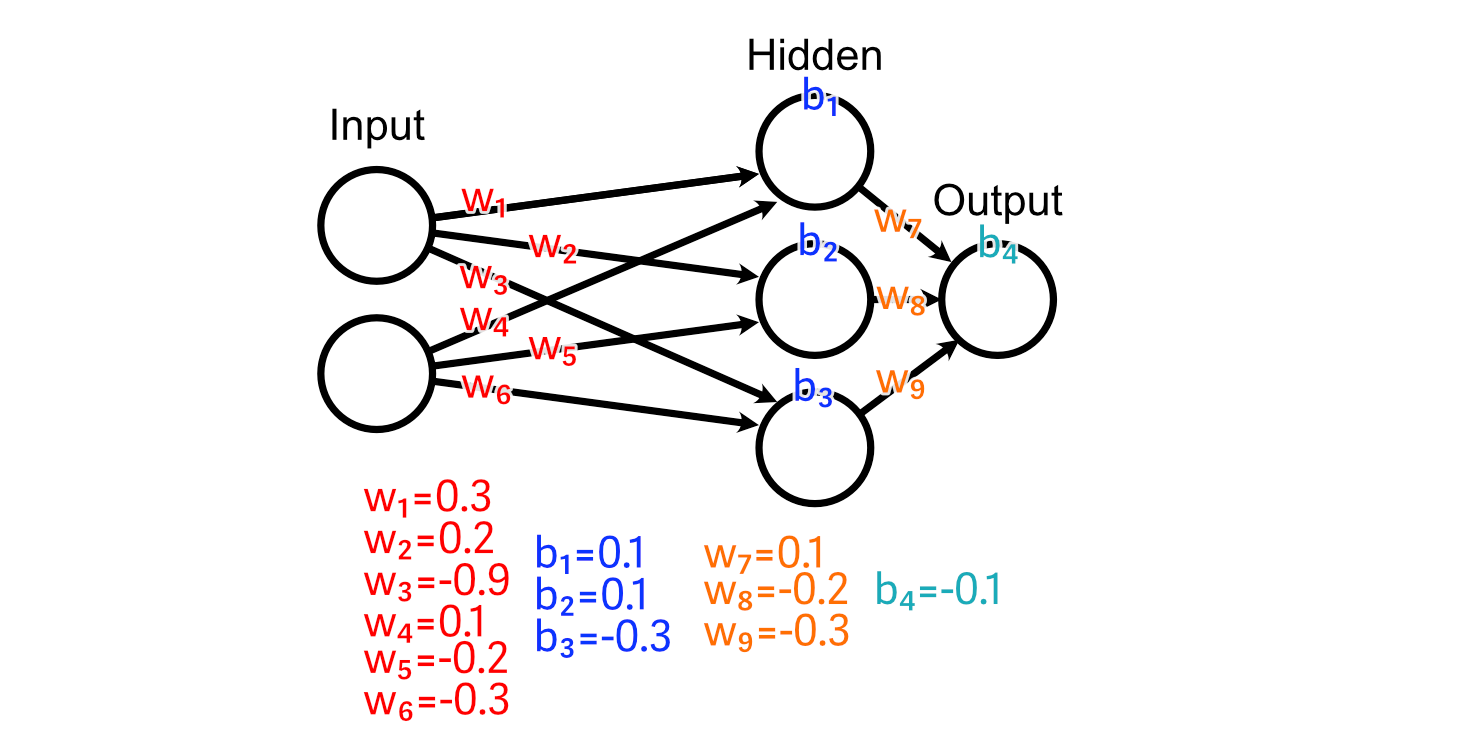
Every of those layers are linked along with, initially, fully random weights.

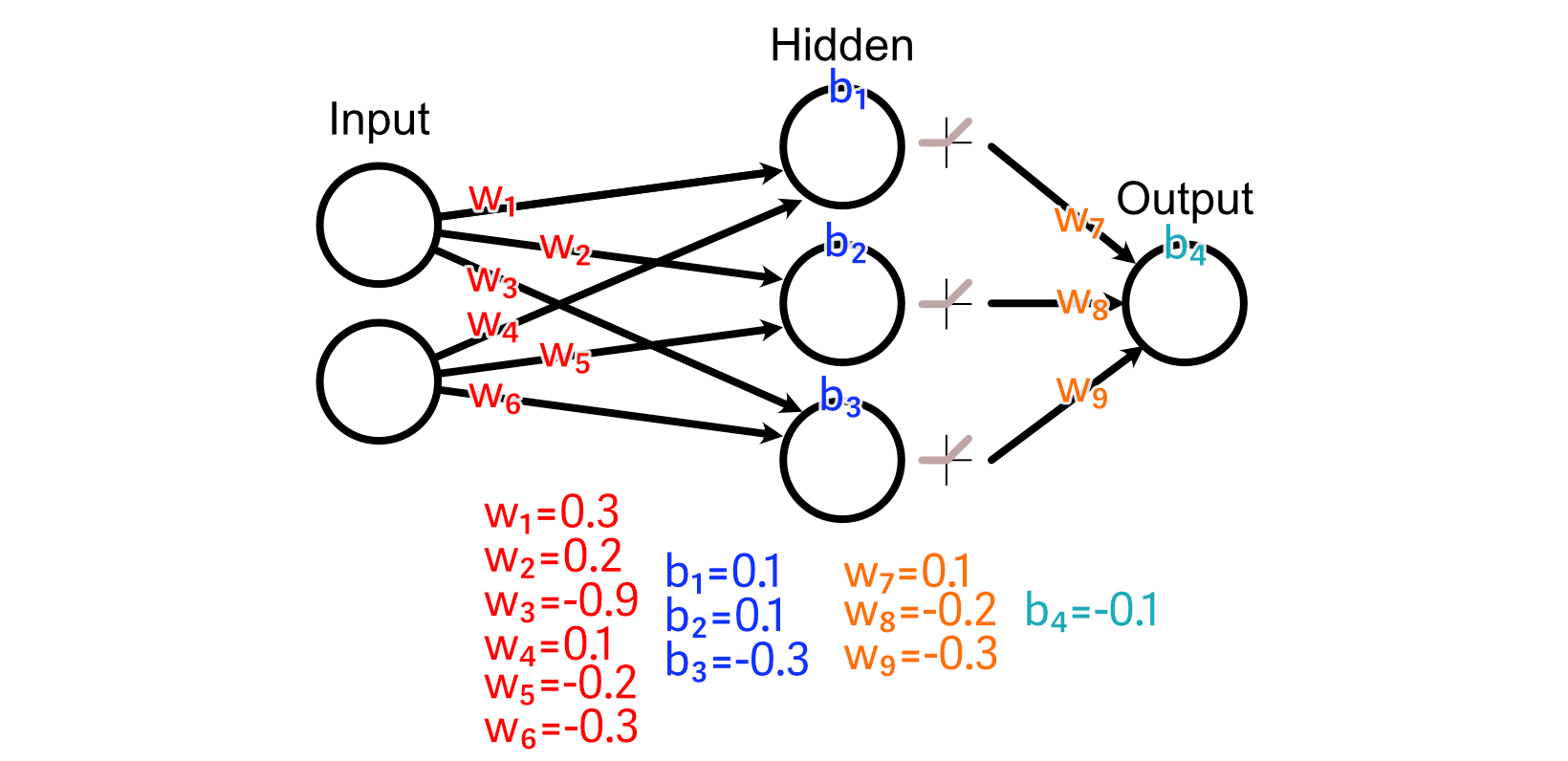
And we’ll use a ReLU activation perform on our hidden layer.

Let’s say we have now some coaching information, through which the specified output is the common worth of the enter.

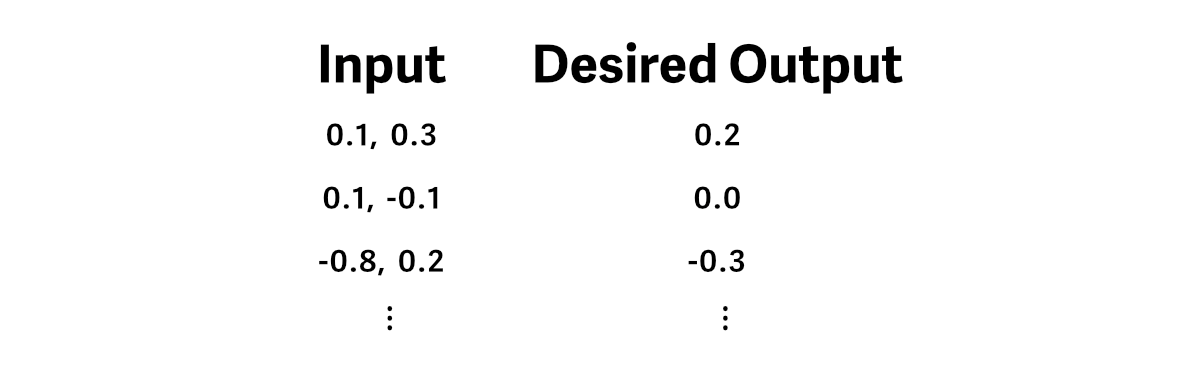
And we cross an instance of our coaching information by the mannequin, producing a prediction.

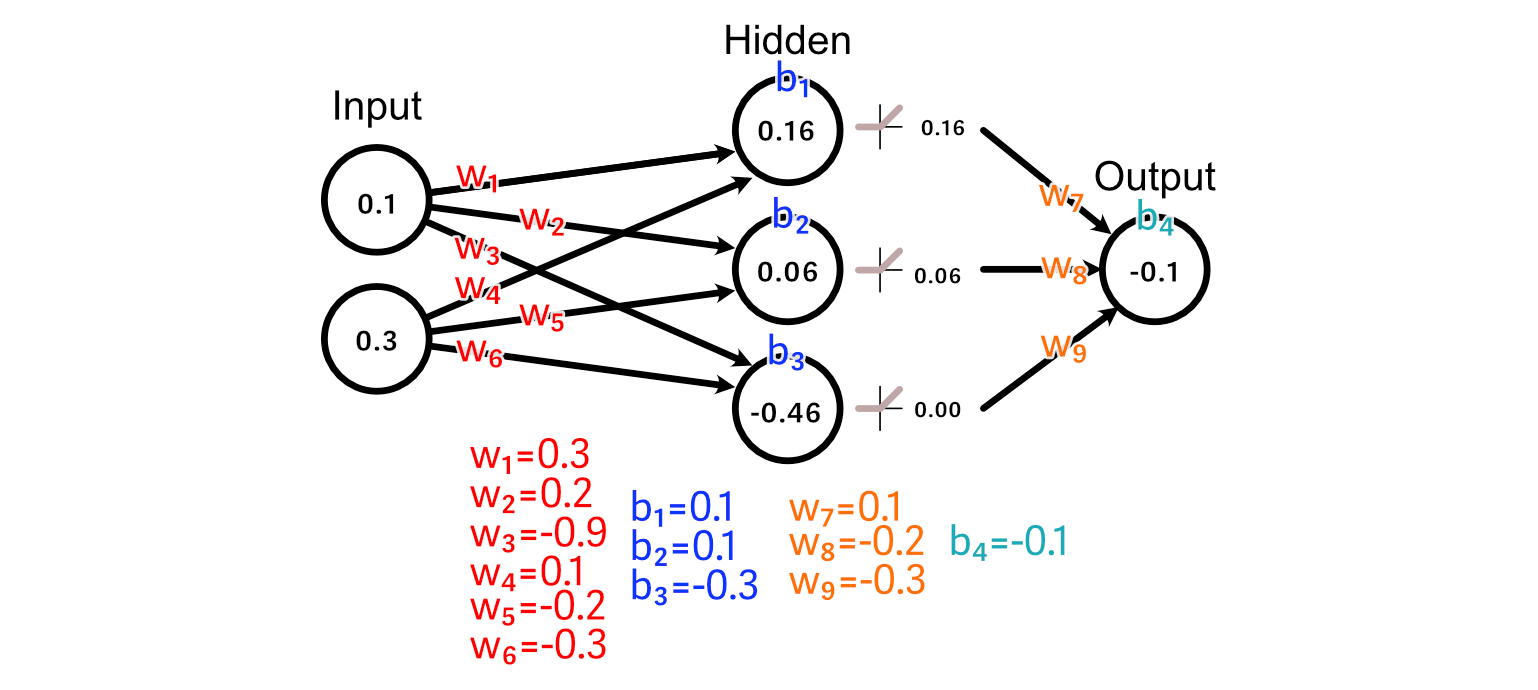
To make our neural community higher on the process of calculating the common of the enter, we first examine the expected output to what our desired output is.

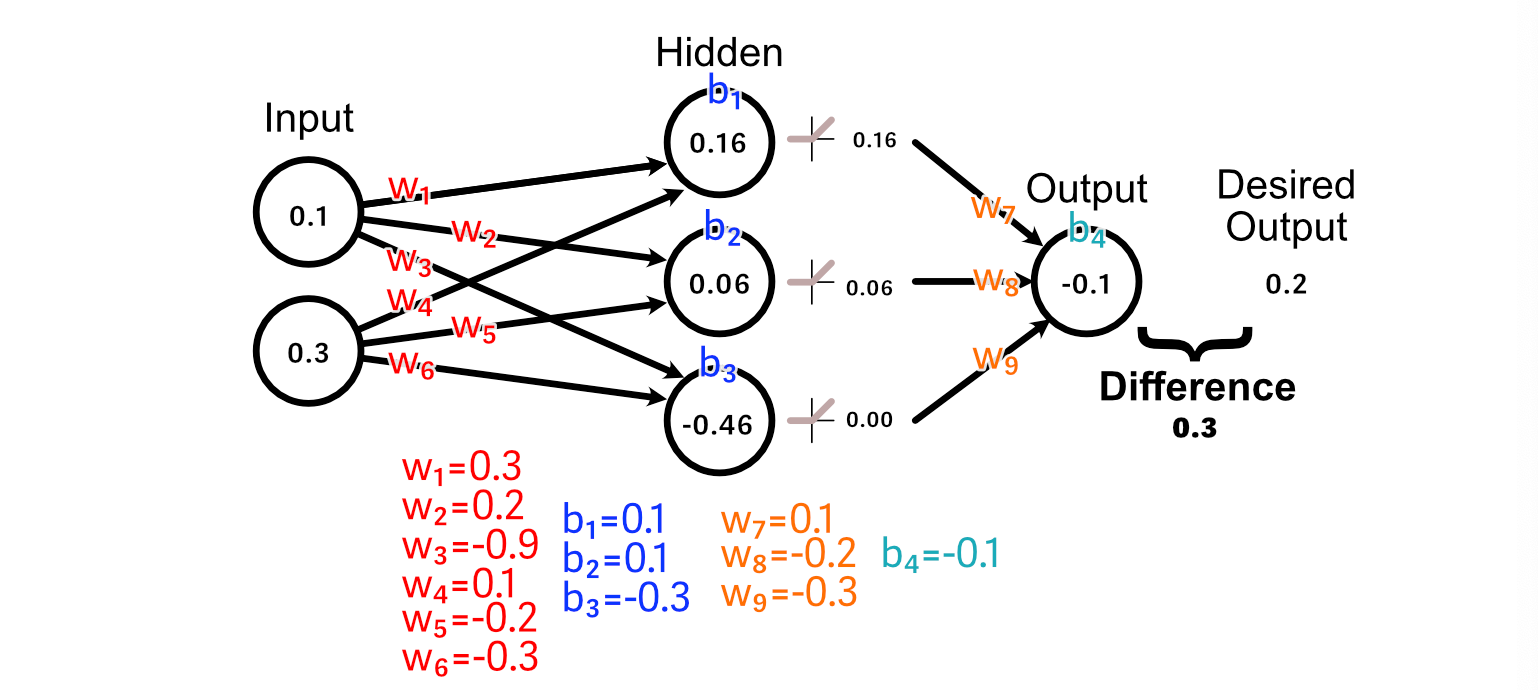
Now that we all know that the output ought to improve in measurement, we are able to look again by the mannequin to calculate how our weights and biases would possibly change to advertise that change.

First, let’s have a look at the weights main instantly into the output: w₇, w₈, w₉. As a result of the output of the third hidden perceptron was -0.46, the activation from ReLU was 0.00.

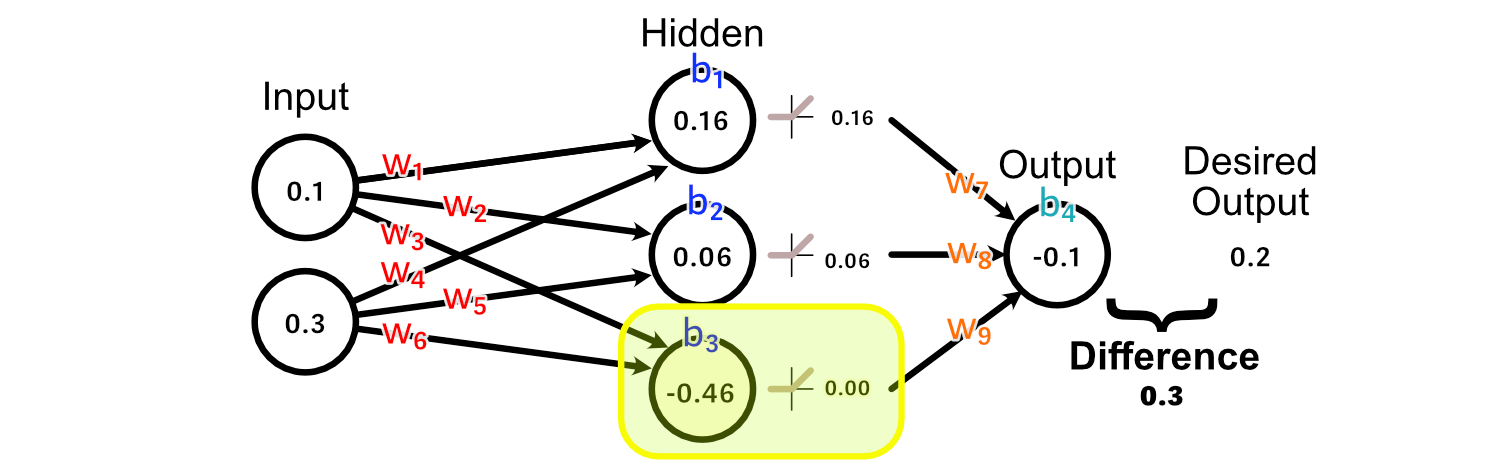
In consequence, there’s no change to w₉ that would outcome us getting nearer to our desired output, as a result of each worth of w₉ would lead to a change of zero on this specific instance.

The second hidden neuron, nevertheless, does have an activated output which is bigger than zero, and thus adjusting w₈ will have an effect on the output for this instance.

The best way we truly calculate how a lot w₈ ought to change is by multiplying how a lot the output ought to change, occasions the enter to w₈.

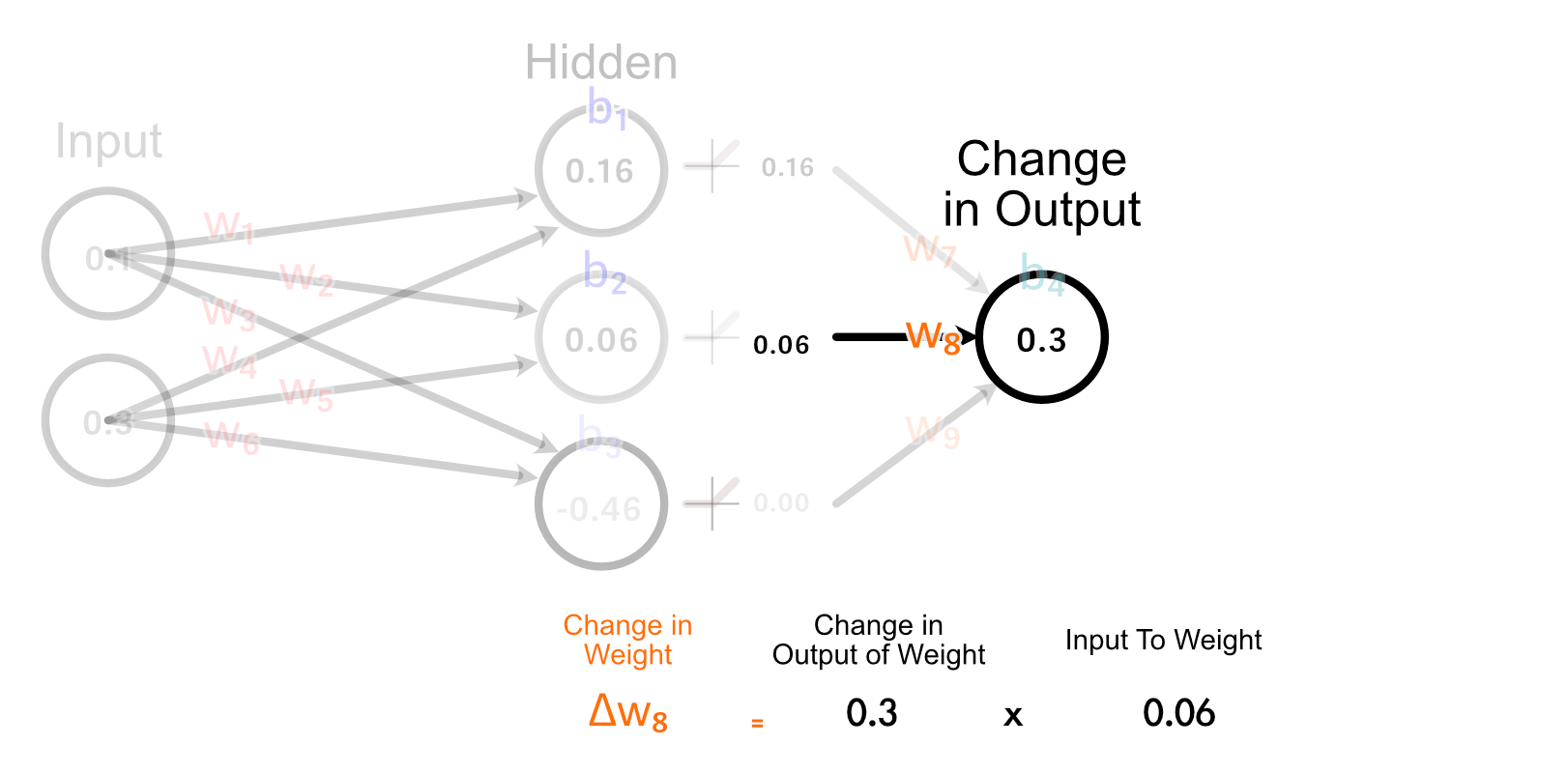
The best clarification of why we do it this manner is “as a result of calculus”, but when we have a look at how all weights get up to date within the final layer, we are able to type a enjoyable instinct.

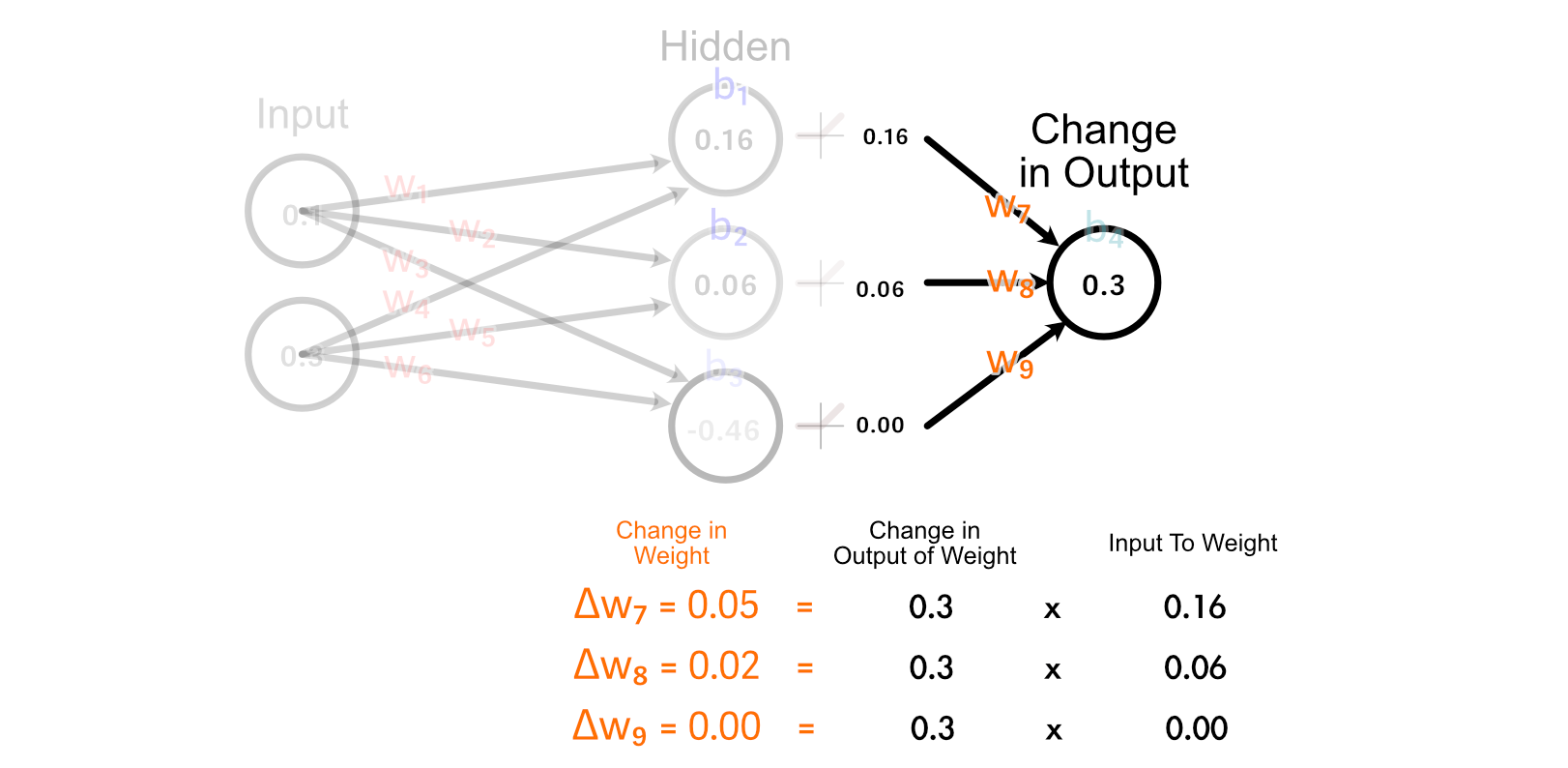
Discover how the 2 perceptrons that “fireplace” (have an output larger than zero) are up to date collectively. Additionally, discover how the stronger a perceptrons output is, the extra its corresponding weight is up to date. That is considerably just like the concept “Neurons that fireside collectively, wire collectively” throughout the human mind.

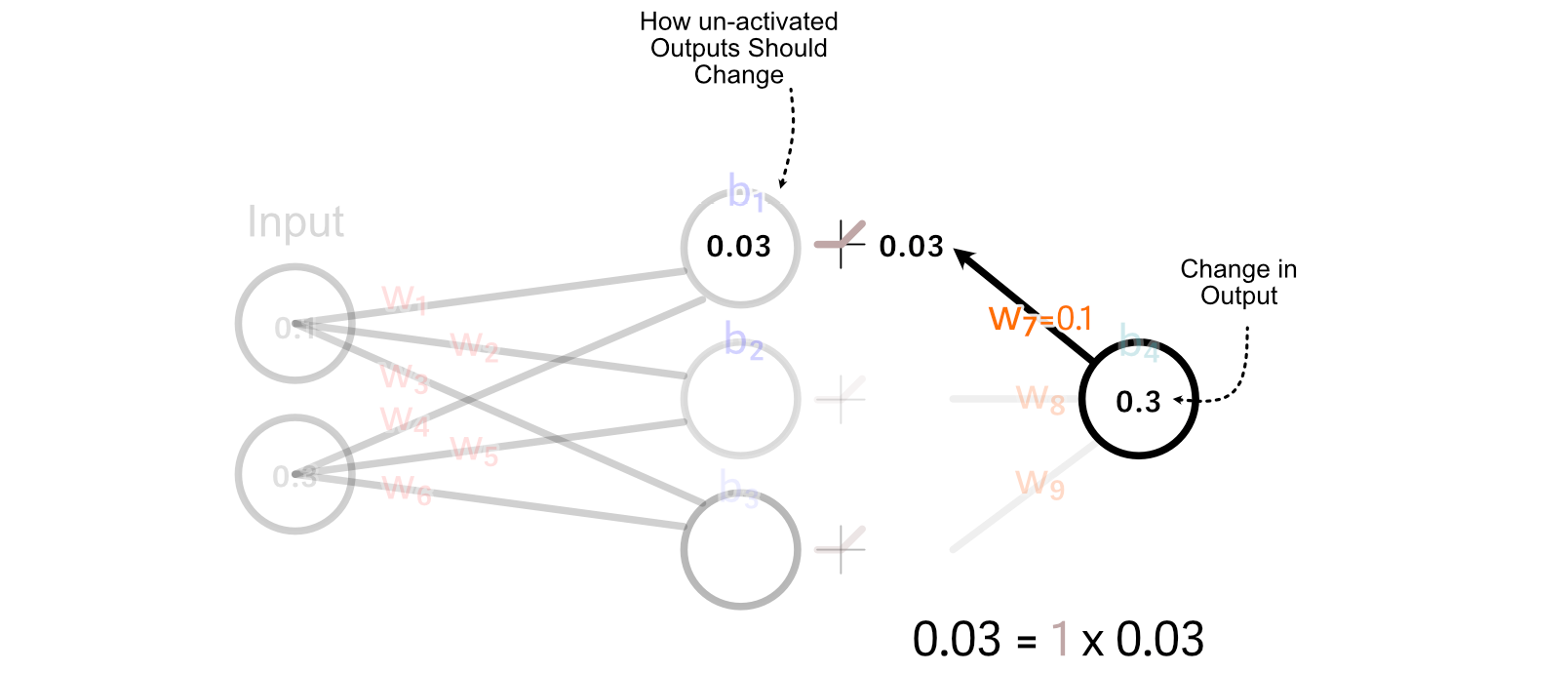
Calculating the change to the output bias is tremendous simple. In truth, we’ve already finished it. As a result of the bias is how a lot a perceptrons output ought to change, the change within the bias is simply the modified within the desired output. So, Δb₄=0.3

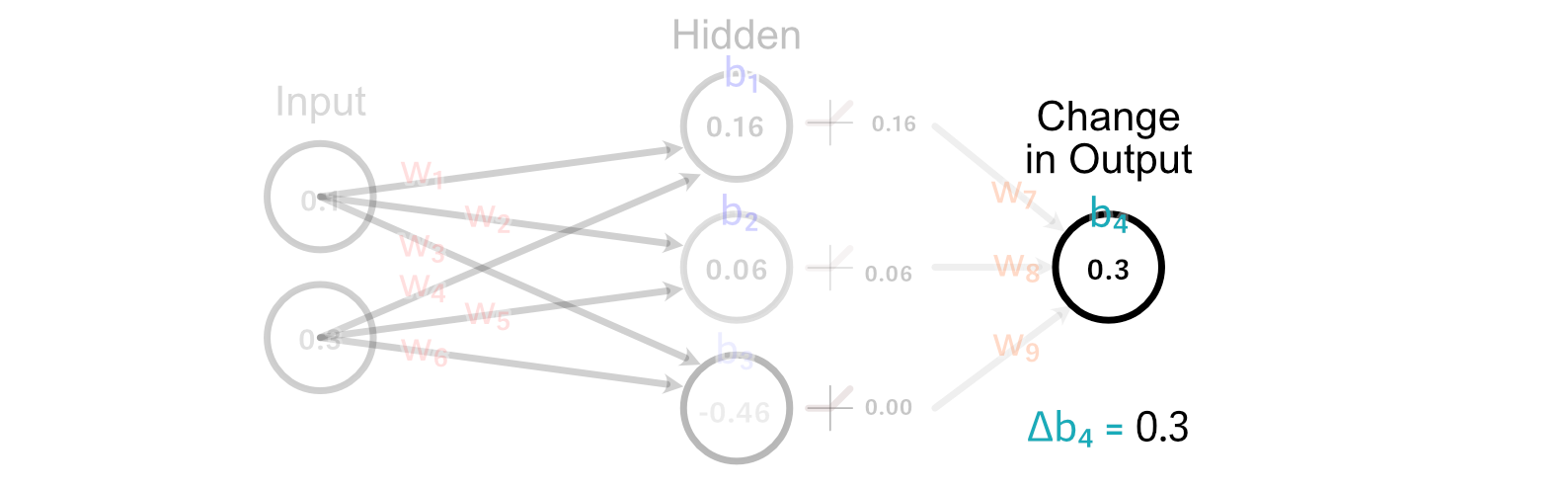
Now that we’ve calculated how the weights and bias of the output perceptron ought to change, we are able to “again propagate” our desired change in output by the mannequin. Let’s begin with again propagating so we are able to calculate how we should always replace w₁.

First, we calculate how the activated output of the of the primary hidden neuron ought to change. We do this by multiplying the change in output by w₇.

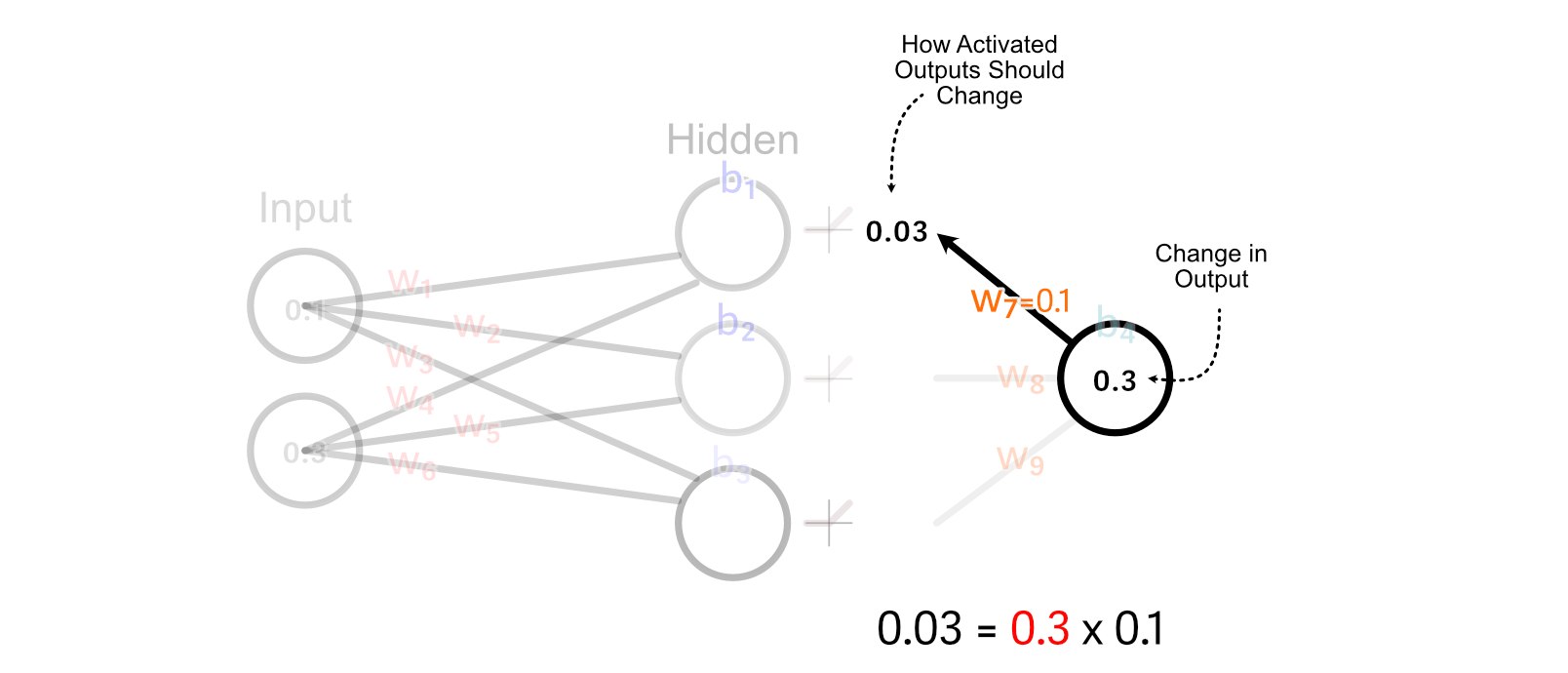
For values which are larger than zero, ReLU merely multiplies these values by 1. So, for this instance, the change we would like the un-activated worth of the primary hidden neuron is the same as the specified change within the activated output

Recall that we calculated the right way to replace w₇ primarily based on multiplying it’s enter by the change in its desired output. We will do the identical factor to calculate the change in w₁.

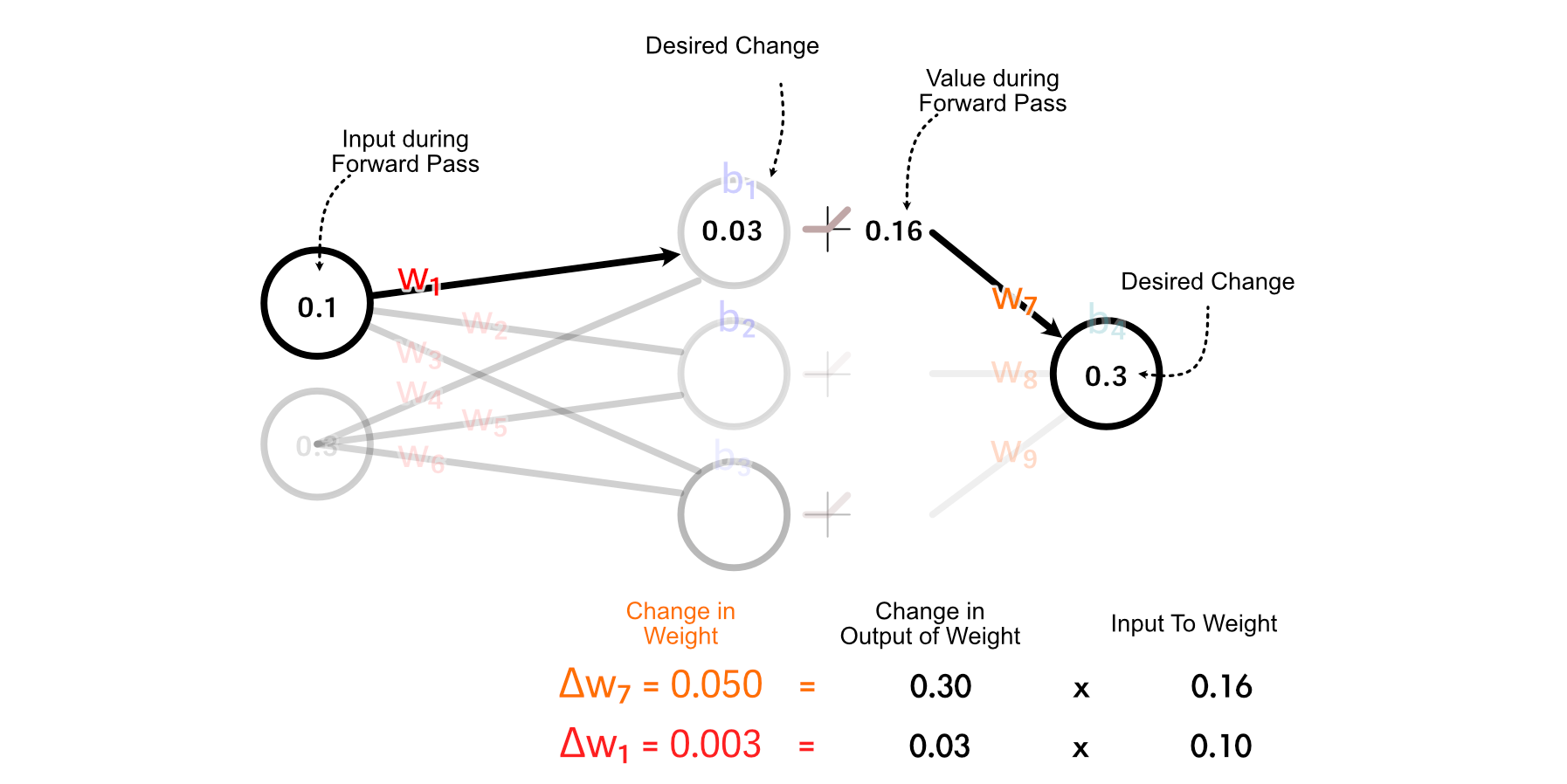
It’s necessary to notice, we’re not truly updating any of the weights or biases all through this course of. Fairly, we’re taking a tally of how we should always replace every parameter, assuming no different parameters are up to date.

So, we are able to do these calculations to calculate all parameter adjustments.

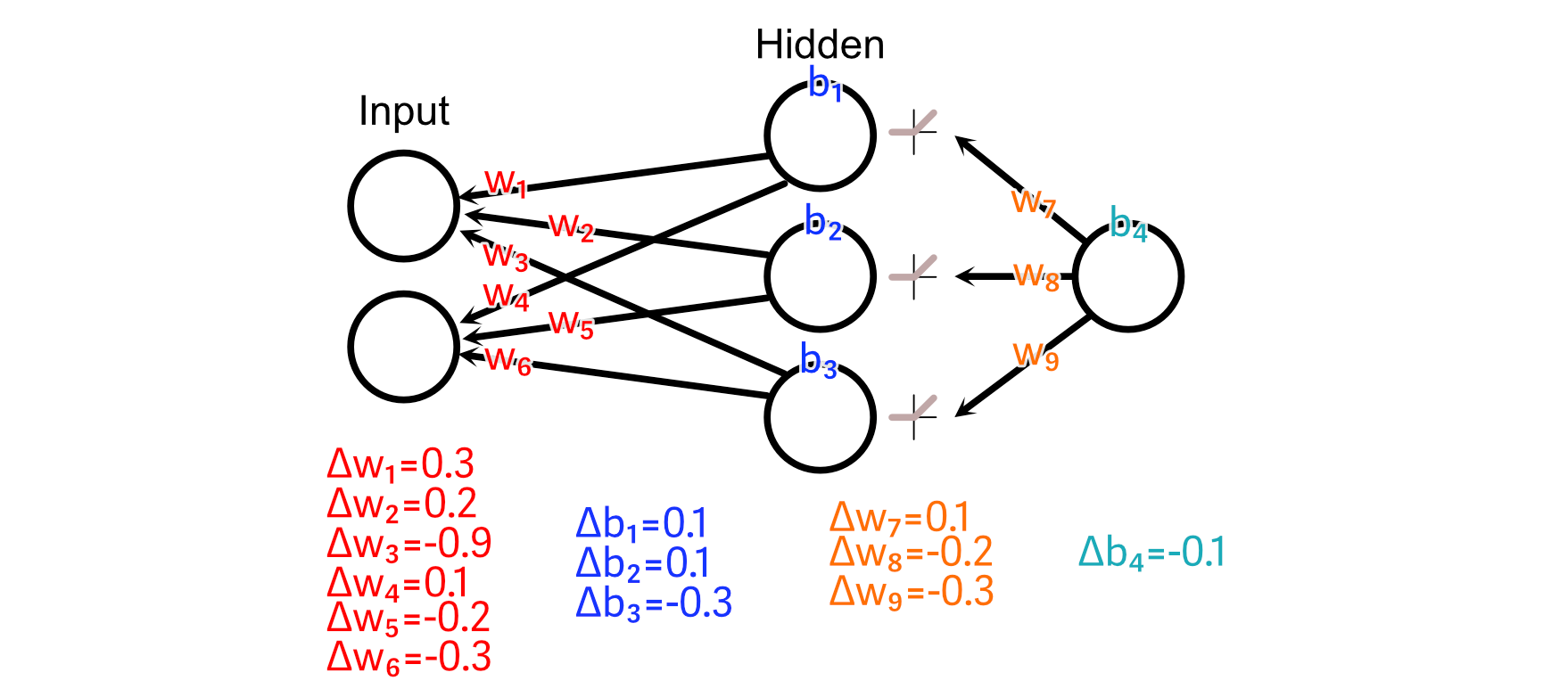
A basic thought of again propagation known as “Studying Charge”, which issues the scale of the adjustments we make to neural networks primarily based on a specific batch of knowledge. To clarify why that is necessary, I’d like to make use of an analogy.

Think about you went outdoors sooner or later, and everybody carrying a hat gave you a humorous look. You most likely don’t wish to soar to the conclusion that carrying hat = humorous look , however you may be a bit skeptical of individuals carrying hats. After three, 4, 5 days, a month, or perhaps a 12 months, if it looks as if the overwhelming majority of individuals carrying hats are providing you with a humorous look, you might start thinking about {that a} robust pattern.

Equally, once we prepare a neural community, we don’t wish to fully change how the neural community thinks primarily based on a single coaching instance. Fairly, we would like every batch to solely incrementally change how the mannequin thinks. As we expose the mannequin to many examples, we’d hope that the mannequin would be taught necessary developments throughout the information.

After we’ve calculated how every parameter ought to change as if it had been the one parameter being up to date, we are able to multiply all these adjustments by a small quantity, like 0.001 , earlier than making use of these adjustments to the parameters. This small quantity is often known as the “studying charge”, and the precise worth it ought to have relies on the mannequin we’re coaching on. This successfully scales down our changes earlier than making use of them to the mannequin.

At this level we lined just about every part one would wish to know to implement a neural community. Let’s give it a shot!

Implementing a Neural Community from Scratch

Usually, an information scientist would simply use a library like PyTorch to implement a neural community in a couple of traces of code, however we’ll be defining a neural community from the bottom up utilizing NumPy, a numerical computing library.

First, let’s begin with a strategy to outline the construction of the neural community.

"""Blocking out the construction of the Neural Community
"""

import numpy as np

class SimpleNN:
    def __init__(self, structure):
        self.structure = structure
        self.weights = []
        self.biases = []

        # Initialize weights and biases
        np.random.seed(99)
        for i in vary(len(structure) - 1):
            self.weights.append(np.random.uniform(
                low=-1, excessive=1,
                measurement=(structure[i], structure[i+1])
            ))
            self.biases.append(np.zeros((1, structure[i+1])))

structure = [2, 64, 64, 64, 1]  # Two inputs, two hidden layers, one output
mannequin = SimpleNN(structure)

print('weight dimensions:')
for w in mannequin.weights:
    print(w.form)

print('nbias dimensions:')
for b in mannequin.biases:
    print(b.form)

Whereas we sometimes draw neural networks as a dense net in actuality we signify the weights between their connections as matrices. That is handy as a result of matrix multiplication, then, is equal to passing information by a neural community.

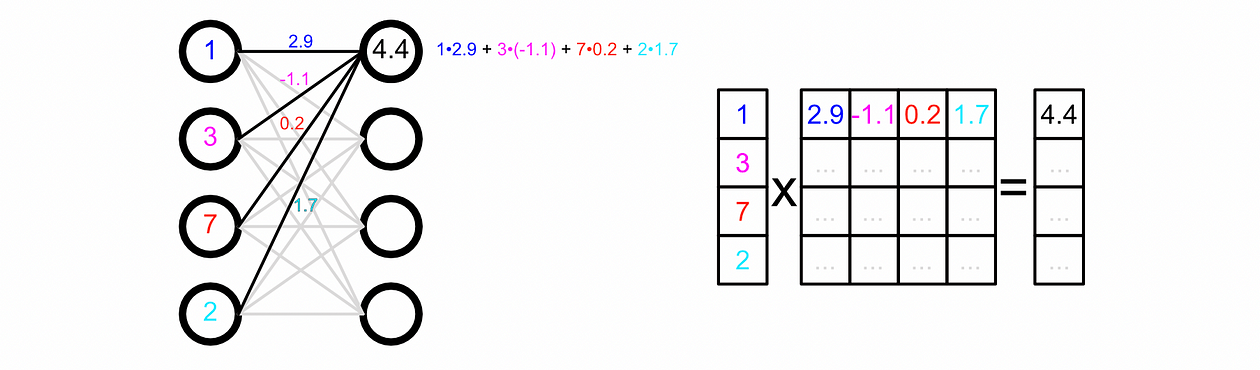
We will make our mannequin make a prediction primarily based on some enter by passing the enter by every layer.

"""Implementing the Ahead Move
"""

import numpy as np

class SimpleNN:
    def __init__(self, structure):
        self.structure = structure
        self.weights = []
        self.biases = []

        # Initialize weights and biases
        np.random.seed(99)
        for i in vary(len(structure) - 1):
            self.weights.append(np.random.uniform(
                low=-1, excessive=1,
                measurement=(structure[i], structure[i+1])
            ))
            self.biases.append(np.zeros((1, structure[i+1])))

    @staticmethod
    def relu(x):
        #implementing the relu activation perform
        return np.most(0, x)

    def ahead(self, X):
        #iterating by all layers
        for W, b in zip(self.weights, self.biases):

            #making use of the load and bias of the layer
            X = np.dot(X, W) + b

            #doing ReLU for all however the final layer
            if W shouldn't be self.weights[-1]:
                X = self.relu(X)

        #returning the outcome
        return X

    def predict(self, X):
        y = self.ahead(X)
        return y.flatten()

#defining a mannequin
structure = [2, 64, 64, 64, 1]  # Two inputs, two hidden layers, one output
mannequin = SimpleNN(structure)

# Generate predictions
prediction = mannequin.predict(np.array([0.1,0.2]))
print(prediction)

We want to have the ability to prepare this mannequin, and to try this we’ll first want an issue to coach the mannequin on. I outlined a random perform that takes in two inputs and leads to an output:

"""Defining what we would like the mannequin to be taught
"""
import numpy as np
import matplotlib.pyplot as plt

# Outline a random perform with two inputs
def random_function(x, y):
    return (np.sin(x) + x * np.cos(y) + y + 3**(x/3))

# Generate a grid of x and y values
x = np.linspace(-10, 10, 100)
y = np.linspace(-10, 10, 100)
X, Y = np.meshgrid(x, y)

# Compute the output of the random perform
Z = random_function(X, Y)

# Create a 2D plot
plt.determine(figsize=(8, 6))
contour = plt.contourf(X, Y, Z, cmap='viridis')
plt.colorbar(contour, label='Operate Worth')
plt.title('2D Plot of Goal Operate')
plt.xlabel('X-axis')
plt.ylabel('Y-axis')
plt.present()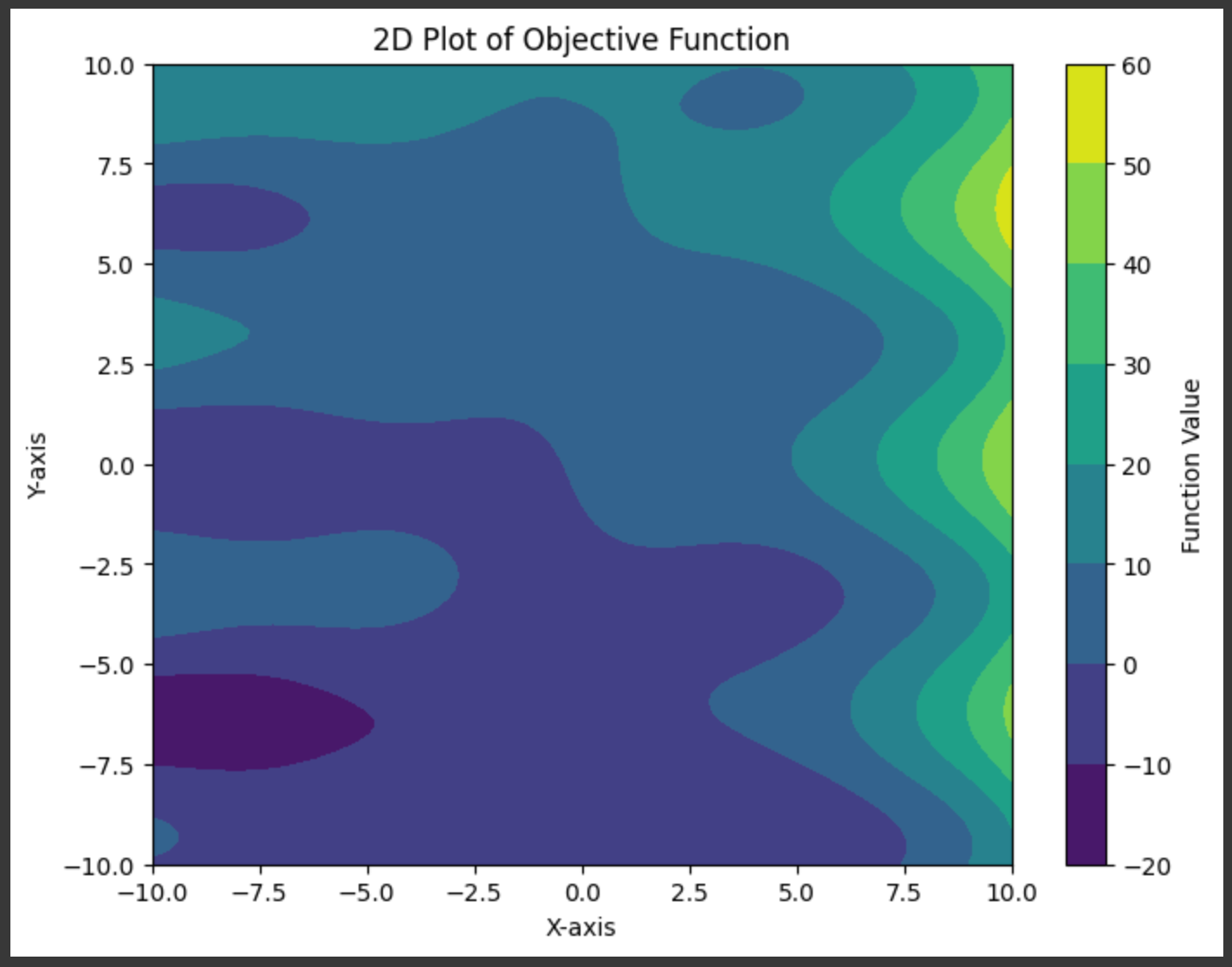

In the actual world we wouldn’t know the underlying perform. We will mimic that actuality by making a dataset consisting of random factors:

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

# Outline a random perform with two inputs
def random_function(x, y):
    return (np.sin(x) + x * np.cos(y) + y + 3**(x/3))

# Outline the variety of random samples to generate
n_samples = 1000

# Generate random X and Y values inside a specified vary
x_min, x_max = -10, 10
y_min, y_max = -10, 10

# Generate random values for X and Y
X_random = np.random.uniform(x_min, x_max, n_samples)
Y_random = np.random.uniform(y_min, y_max, n_samples)

# Consider the random perform on the generated X and Y values
Z_random = random_function(X_random, Y_random)

# Create a dataset
dataset = pd.DataFrame({
    'X': X_random,
    'Y': Y_random,
    'Z': Z_random
})

# Show the dataset
print(dataset.head())

# Create a 2D scatter plot of the sampled information
plt.determine(figsize=(8, 6))
scatter = plt.scatter(dataset['X'], dataset['Y'], c=dataset['Z'], cmap='viridis', s=10)
plt.colorbar(scatter, label='Operate Worth')
plt.title('Scatter Plot of Randomly Sampled Knowledge')
plt.xlabel('X-axis')
plt.ylabel('Y-axis')
plt.present()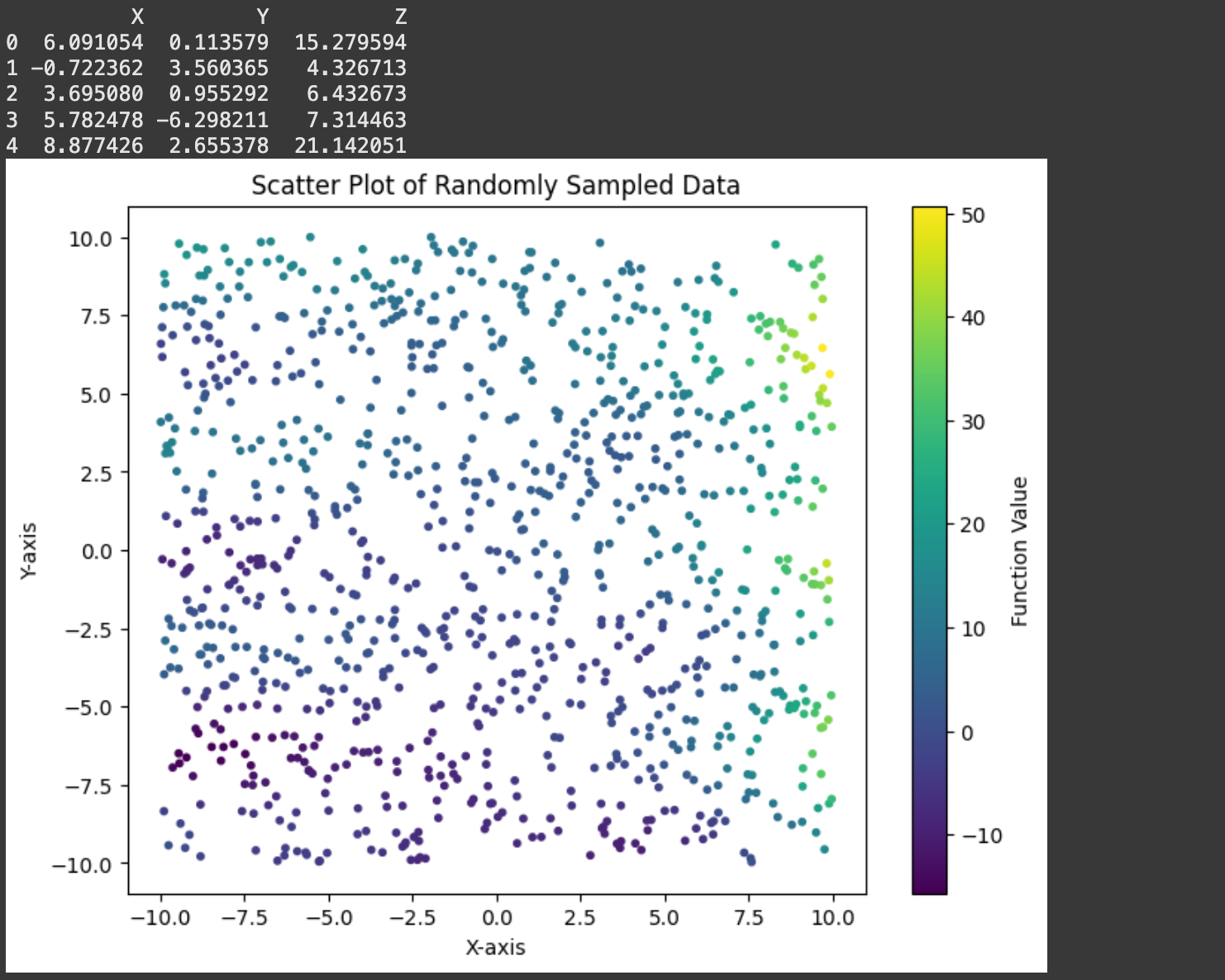

Recall that the again propagation algorithm updates parameters primarily based on what occurs in a ahead cross. So, earlier than we implement backpropagation itself, let’s maintain observe of some necessary values within the ahead cross: The inputs and outputs of every perceptron all through the mannequin.

import numpy as np

class SimpleNN:
    def __init__(self, structure):
        self.structure = structure
        self.weights = []
        self.biases = []

        #protecting observe of those values on this code block
        #so we are able to observe them
        self.perceptron_inputs = None
        self.perceptron_outputs = None

        # Initialize weights and biases
        np.random.seed(99)
        for i in vary(len(structure) - 1):
            self.weights.append(np.random.uniform(
                low=-1, excessive=1,
                measurement=(structure[i], structure[i+1])
            ))
            self.biases.append(np.zeros((1, structure[i+1])))

    @staticmethod
    def relu(x):
        return np.most(0, x)

    def ahead(self, X):
        self.perceptron_inputs = [X]
        self.perceptron_outputs = []

        for W, b in zip(self.weights, self.biases):
            Z = np.dot(self.perceptron_inputs[-1], W) + b
            self.perceptron_outputs.append(Z)

            if W is self.weights[-1]:  # Final layer (output)
                A = Z  # Linear output for regression
            else:
                A = self.relu(Z)
            self.perceptron_inputs.append(A)

        return self.perceptron_inputs, self.perceptron_outputs

    def predict(self, X):
        perceptron_inputs, _ = self.ahead(X)
        return perceptron_inputs[-1].flatten()

#defining a mannequin
structure = [2, 64, 64, 64, 1]  # Two inputs, two hidden layers, one output
mannequin = SimpleNN(structure)

# Generate predictions
prediction = mannequin.predict(np.array([0.1,0.2]))

#wanting by vital optimization values
for i, (inpt, outpt) in enumerate(zip(mannequin.perceptron_inputs, mannequin.perceptron_outputs[:-1])):
    print(f'layer {i}')
    print(f'enter: {inpt.form}')
    print(f'output: {outpt.form}')
    print('')

print('Closing Output:')
print(mannequin.perceptron_outputs[-1].form)

Now that we have now a report saved of vital middleman worth throughout the community, we are able to use these values, together with the error of a mannequin for a specific prediction, to calculate the adjustments we should always make to the mannequin.

import numpy as np

class SimpleNN:
    def __init__(self, structure):
        self.structure = structure
        self.weights = []
        self.biases = []

        # Initialize weights and biases
        np.random.seed(99)
        for i in vary(len(structure) - 1):
            self.weights.append(np.random.uniform(
                low=-1, excessive=1,
                measurement=(structure[i], structure[i+1])
            ))
            self.biases.append(np.zeros((1, structure[i+1])))

    @staticmethod
    def relu(x):
        return np.most(0, x)

    @staticmethod
    def relu_as_weights(x):
        return (x > 0).astype(float)

    def ahead(self, X):
        perceptron_inputs = [X]
        perceptron_outputs = []

        for W, b in zip(self.weights, self.biases):
            Z = np.dot(perceptron_inputs[-1], W) + b
            perceptron_outputs.append(Z)

            if W is self.weights[-1]:  # Final layer (output)
                A = Z  # Linear output for regression
            else:
                A = self.relu(Z)
            perceptron_inputs.append(A)

        return perceptron_inputs, perceptron_outputs

    def backward(self, perceptron_inputs, perceptron_outputs, goal):
        weight_changes = []
        bias_changes = []

        m = len(goal)
        dA = perceptron_inputs[-1] - goal.reshape(-1, 1)  # Output layer gradient

        for i in reversed(vary(len(self.weights))):
            dZ = dA if i == len(self.weights) - 1 else dA * self.relu_as_weights(perceptron_outputs[i])
            dW = np.dot(perceptron_inputs[i].T, dZ) / m
            db = np.sum(dZ, axis=0, keepdims=True) / m
            weight_changes.append(dW)
            bias_changes.append(db)

            if i > 0:
                dA = np.dot(dZ, self.weights[i].T)

        return record(reversed(weight_changes)), record(reversed(bias_changes))

    def predict(self, X):
        perceptron_inputs, _ = self.ahead(X)
        return perceptron_inputs[-1].flatten()

#defining a mannequin
structure = [2, 64, 64, 64, 1]  # Two inputs, two hidden layers, one output
mannequin = SimpleNN(structure)

#defining a pattern enter and goal output
enter = np.array([[0.1,0.2]])
desired_output = np.array([0.5])

#doing ahead and backward cross to calculate adjustments
perceptron_inputs, perceptron_outputs = mannequin.ahead(enter)
weight_changes, bias_changes = mannequin.backward(perceptron_inputs, perceptron_outputs, desired_output)

#smaller numbers for printing
np.set_printoptions(precision=2)

for i, (layer_weights, layer_biases, layer_weight_changes, layer_bias_changes)
in enumerate(zip(mannequin.weights, mannequin.biases, weight_changes, bias_changes)):
    print(f'layer {i}')
    print(f'weight matrix: {layer_weights.form}')
    print(f'weight matrix adjustments: {layer_weight_changes.form}')
    print(f'bias matrix: {layer_biases.form}')
    print(f'bias matrix adjustments: {layer_bias_changes.form}')
    print('')

print('The load and weight change matrix of the second layer:')
print('weight matrix:')
print(mannequin.weights[1])
print('change matrix:')
print(weight_changes[1])

That is most likely probably the most complicated implementation step, so I wish to take a second to dig by a number of the particulars. The elemental thought is precisely as we described in earlier sections. We’re iterating over all layers, from again to entrance, and calculating what change to every weight and bias would lead to a greater output.

# calculating output error
dA = perceptron_inputs[-1] - goal.reshape(-1, 1)

#a scaling issue for the batch measurement.
#you need adjustments to be a median throughout all batches
#so we divide by m as soon as we have aggregated all adjustments.
m = len(goal)

for i in reversed(vary(len(self.weights))):
  dZ = dA #simplified for now

  # calculating change to weights
  dW = np.dot(perceptron_inputs[i].T, dZ) / m
  # calculating change to bias
  db = np.sum(dZ, axis=0, keepdims=True) / m

  # protecting observe of required adjustments
  weight_changes.append(dW)
  bias_changes.append(db)
  ...

Calculating the change to bias is fairly straight ahead. In the event you have a look at how the output of a given neuron ought to have impacted all future neurons, you may add up all these values (that are each constructive and adverse) to get an thought of if the neuron ought to be biased in a constructive or adverse course.

The best way we calculate the change to weights, through the use of matrix multiplication, is a little more mathematically complicated.

dW = np.dot(perceptron_inputs[i].T, dZ) / m

Principally, this line says that the change within the weight ought to be equal to the worth going into the perceptron, occasions how a lot the output ought to have modified. If a perceptron had a giant enter, the change to its outgoing weights ought to be a big magnitude, if the perceptron had a small enter, the change to its outgoing weights will probably be small. Additionally, if a weight factors in the direction of an output which ought to change so much, the load ought to change so much.

There’s one other line we should always focus on in our again propagation implement.

dZ = dA if i == len(self.weights) - 1 else dA * self.relu_as_weights(perceptron_outputs[i])

On this specific community, there are activation capabilities all through the community, following all however the ultimate output. After we do again propagation, we have to back-propagate by these activation capabilities in order that we are able to replace the neurons which lie earlier than them. We do that for all however the final layer, which doesn’t have an activation perform, which is why dZ = dA if i == len(self.weights) - 1 .

In fancy math converse we’d name this a spinoff, however as a result of I don’t wish to get into calculus, I known as the perform relu_as_weights . Principally, we are able to deal with every of our ReLU activations as one thing like a tiny neural community, who’s weight is a perform of the enter. If the enter of the ReLU activation perform is lower than zero, then that’s like passing that enter by a neural community with a weight of zero. If the enter of ReLU is bigger than zero, then that’s like passing the enter by a neural netowork with a weight of 1.

That is precisely what the relu_as_weights perform does.

def relu_as_weights(x):
        return (x > 0).astype(float)

Utilizing this logic we are able to deal with again propagating by ReLU similar to we again propagate by the remainder of the neural community.

Once more, I’ll be masking this idea from a extra strong mathematical potential quickly, however that’s the important thought from a conceptual perspective.

Now that we have now the ahead and backward cross carried out, we are able to implement coaching the mannequin.

import numpy as np

class SimpleNN:
    def __init__(self, structure):
        self.structure = structure
        self.weights = []
        self.biases = []

        # Initialize weights and biases
        np.random.seed(99)
        for i in vary(len(structure) - 1):
            self.weights.append(np.random.uniform(
                low=-1, excessive=1,
                measurement=(structure[i], structure[i+1])
            ))
            self.biases.append(np.zeros((1, structure[i+1])))

    @staticmethod
    def relu(x):
        return np.most(0, x)

    @staticmethod
    def relu_as_weights(x):
        return (x > 0).astype(float)

    def ahead(self, X):
        perceptron_inputs = [X]
        perceptron_outputs = []

        for W, b in zip(self.weights, self.biases):
            Z = np.dot(perceptron_inputs[-1], W) + b
            perceptron_outputs.append(Z)

            if W is self.weights[-1]:  # Final layer (output)
                A = Z  # Linear output for regression
            else:
                A = self.relu(Z)
            perceptron_inputs.append(A)

        return perceptron_inputs, perceptron_outputs

    def backward(self, perceptron_inputs, perceptron_outputs, y_true):
        weight_changes = []
        bias_changes = []

        m = len(y_true)
        dA = perceptron_inputs[-1] - y_true.reshape(-1, 1)  # Output layer gradient

        for i in reversed(vary(len(self.weights))):
            dZ = dA if i == len(self.weights) - 1 else dA * self.relu_as_weights(perceptron_outputs[i])
            dW = np.dot(perceptron_inputs[i].T, dZ) / m
            db = np.sum(dZ, axis=0, keepdims=True) / m
            weight_changes.append(dW)
            bias_changes.append(db)

            if i > 0:
                dA = np.dot(dZ, self.weights[i].T)

        return record(reversed(weight_changes)), record(reversed(bias_changes))

    def update_weights(self, weight_changes, bias_changes, lr):
        for i in vary(len(self.weights)):
            self.weights[i] -= lr * weight_changes[i]
            self.biases[i] -= lr * bias_changes[i]

    def prepare(self, X, y, epochs, lr=0.01):
        for epoch in vary(epochs):
            perceptron_inputs, perceptron_outputs = self.ahead(X)
            weight_changes, bias_changes = self.backward(perceptron_inputs, perceptron_outputs, y)
            self.update_weights(weight_changes, bias_changes, lr)

            if epoch % 20 == 0 or epoch == epochs - 1:
                loss = np.imply((perceptron_inputs[-1].flatten() - y) ** 2)  # MSE
                print(f"EPOCH {epoch}: Loss = {loss:.4f}")

    def predict(self, X):
        perceptron_inputs, _ = self.ahead(X)
        return perceptron_inputs[-1].flatten()

The prepare perform:

• iterates by all the information some variety of occasions (outlined by epoch )
• passes the information by a ahead cross
• calculates how the weights and biases ought to change
• updates the weights and biases, by scaling their adjustments by the educational charge ( lr )

And thus we’ve carried out a neural community! Let’s prepare it.

Coaching and Evaluating the Neural Community.

Recall that we outlined an arbitrary 2D perform we needed to discover ways to emulate,

and we sampled that house with some variety of factors, which we’re utilizing to coach the mannequin.

Earlier than feeding this information into our mannequin, it’s important that we first “normalize” the information. Sure values of the dataset are very small or very massive, which may make coaching a neural community very troublesome. Values throughout the neural community can shortly develop to absurdly massive values, or diminish to zero, which may inhibit coaching. Normalization squashes all of our inputs, and our desired outputs, right into a extra cheap vary averaging round zero with a standardized distribution known as a “regular” distribution.

# Flatten the information
X_flat = X.flatten()
Y_flat = Y.flatten()
Z_flat = Z.flatten()

# Stack X and Y as enter options
inputs = np.column_stack((X_flat, Y_flat))
outputs = Z_flat

# Normalize the inputs and outputs
inputs_mean = np.imply(inputs, axis=0)
inputs_std = np.std(inputs, axis=0)
outputs_mean = np.imply(outputs)
outputs_std = np.std(outputs)

inputs = (inputs - inputs_mean) / inputs_std
outputs = (outputs - outputs_mean) / outputs_std

If we wish to get again predictions within the precise vary of knowledge from our unique dataset, we are able to use these values to basically “un-squash” the information.

As soon as we’ve finished that, we are able to outline and prepare our mannequin.

# Outline the structure: [input_dim, hidden1, ..., output_dim]
structure = [2, 64, 64, 64, 1]  # Two inputs, two hidden layers, one output
mannequin = SimpleNN(structure)

# Practice the mannequin
mannequin.prepare(inputs, outputs, epochs=2000, lr=0.001)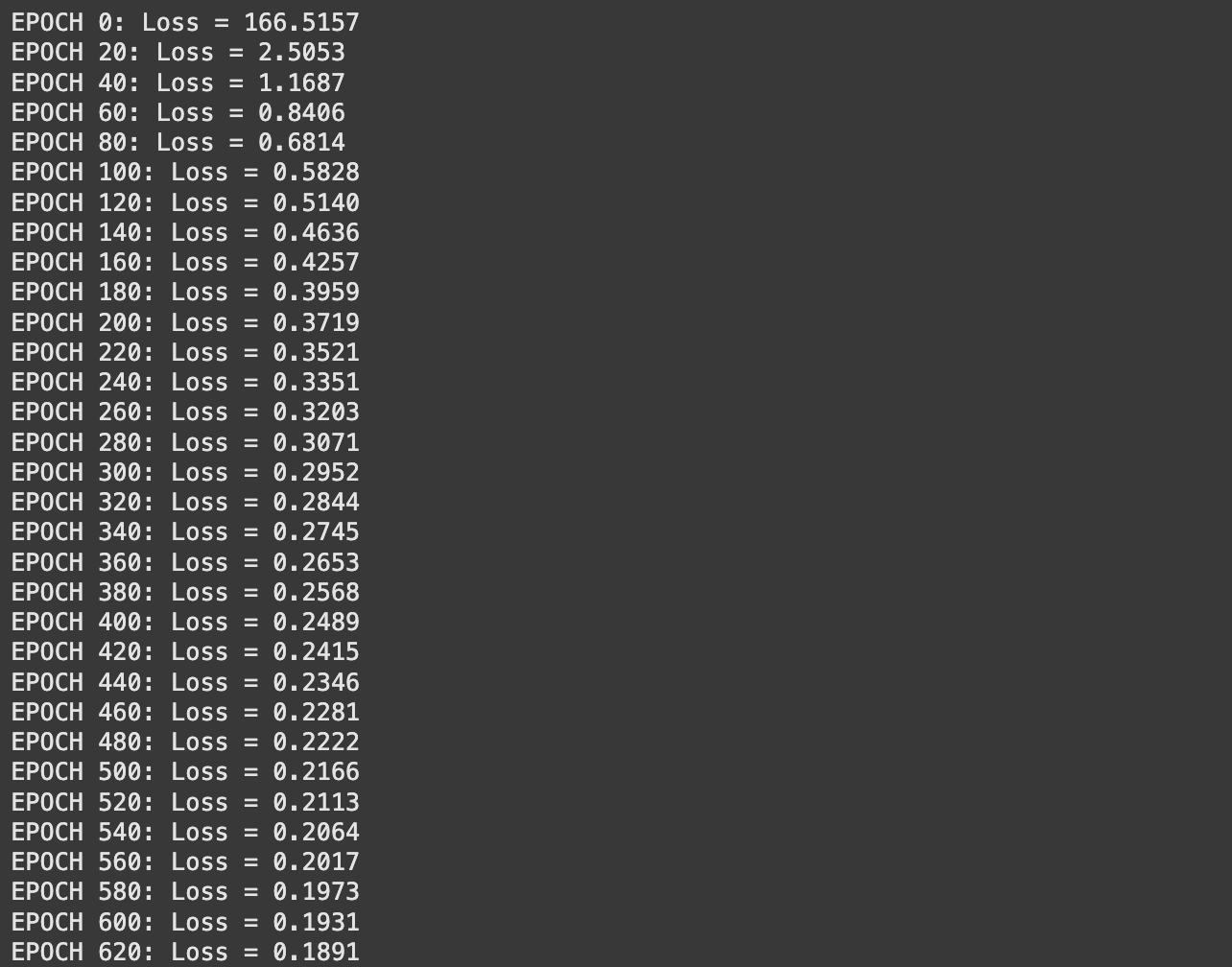

Then we are able to visualize the output of the neural community’s prediction vs the precise perform.

import matplotlib.pyplot as plt

# Reshape predictions to grid format for visualization
Z_pred = mannequin.predict(inputs) * outputs_std + outputs_mean
Z_pred = Z_pred.reshape(X.form)

# Plot comparability of the true perform and the mannequin predictions
fig, axes = plt.subplots(1, 2, figsize=(14, 6))

# Plot the true perform
axes[0].contourf(X, Y, Z, cmap='viridis')
axes[0].set_title("True Operate")
axes[0].set_xlabel("X-axis")
axes[0].set_ylabel("Y-axis")
axes[0].colorbar = plt.colorbar(axes[0].contourf(X, Y, Z, cmap='viridis'), ax=axes[0], label="Operate Worth")

# Plot the expected perform
axes[1].contourf(X, Y, Z_pred, cmap='plasma')
axes[1].set_title("NN Predicted Operate")
axes[1].set_xlabel("X-axis")
axes[1].set_ylabel("Y-axis")
axes[1].colorbar = plt.colorbar(axes[1].contourf(X, Y, Z_pred, cmap='plasma'), ax=axes[1], label="Operate Worth")

plt.tight_layout()
plt.present()

This did an okay job, however not as nice as we would like. That is the place plenty of information scientists spend their time, and there are a ton of approaches to creating a neural community match a sure downside higher. Some apparent ones are:

• use extra information
• mess around with the educational charge
• prepare for extra epochs
• change the construction of the mannequin

It’s fairly simple for us to crank up the quantity of knowledge we’re coaching on. Let’s see the place that leads us. Right here I’m sampling our dataset 10,000 occasions, which is 10x extra coaching samples than our earlier dataset.

After which I educated the mannequin similar to earlier than, besides this time it took so much longer as a result of every epoch now analyses 10,000 samples quite than 1,000.

# Outline the structure: [input_dim, hidden1, ..., output_dim]
structure = [2, 64, 64, 64, 1]  # Two inputs, two hidden layers, one output
mannequin = SimpleNN(structure)

# Practice the mannequin
mannequin.prepare(inputs, outputs, epochs=2000, lr=0.001)

I then rendered the output of this mannequin, the identical approach I did earlier than, but it surely didn’t actually seem like the output bought a lot better.

Trying again on the loss output from coaching, it looks as if the loss remains to be steadily declining. Perhaps I simply want to coach for longer. Let’s attempt that.

# Outline the structure: [input_dim, hidden1, ..., output_dim]
structure = [2, 64, 64, 64, 1]  # Two inputs, two hidden layers, one output
mannequin = SimpleNN(structure)

# Practice the mannequin
mannequin.prepare(inputs, outputs, epochs=4000, lr=0.001)

The outcomes appear to be a bit higher, however they aren’t’ superb.

I’ll spare you the main points. I ran this a couple of occasions, and I bought some respectable outcomes, however by no means something 1 to 1. I’ll be masking some extra superior approaches information scientists use, like annealing and dropout, in future articles which can lead to a extra constant and higher output. Nonetheless, although, we made a neural community from scratch and educated it to do one thing, and it did a good job! Fairly neat!

Conclusion

On this article we prevented calculus just like the plague whereas concurrently forging an understanding of Neural Networks. We explored their concept, a little bit bit in regards to the math, the concept of again propagation, after which carried out a neural community from scratch. We then utilized a neural community to a toy downside, and explored a number of the easy concepts information scientists make use of to really prepare neural networks to be good at issues.

In future articles we’ll discover a couple of extra superior approaches to Neural Networks, so keep tuned! For now, you may be interested by a extra thorough evaluation of Gradients, the basic math behind again propagation.

What Are Gradients, and Why Do They Explode?

You may additionally have an interest on this article, which covers coaching a neural community utilizing extra typical Data Science instruments like PyTorch.

AI for the Absolute Novice – Intuitively and Exhaustively Explained

Be a part of Intuitively and Exhaustively Defined

At IAEE you will discover:

• Lengthy type content material, just like the article you simply learn
• Conceptual breakdowns of a number of the most cutting-edge AI subjects
• By-Hand walkthroughs of vital mathematical operations in AI
• Sensible tutorials and explainers