Since Vaswani et al. (2017), transformers have turn out to be the dominant method in pure language processing(NLP). Nonetheless, convolutional neural networks (CNN) remained the mannequin of selection in pc imaginative and prescient. There have been some makes an attempt to make use of transformers together with CNNs.
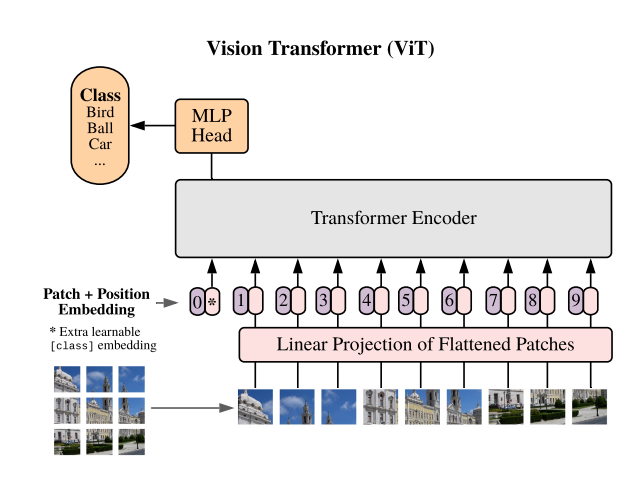
To make use of a pure transformer on imaginative and prescient duties, we should divide photos into patches and supply the linear embeddings of these patches because the enter. Patches are much like tokens in NLP.
Nonetheless, the transformer have to be skilled on a giant information set. Transformer is a generalization of CNNs and thus lacks inductive biases(assumptions concerning the information) corresponding to locality and translation invariance. (We assume that info contained in a picture is targeting native areas and doesn’t change with translations). Thus, transformers lack generalization potential when skilled on a small picture information set.
Consideration is a quadratic operation. Thus, we can not carry out consideration on the pixel degree.
Much like the BERT’s class token, a learnable embedding is prepended. (0 place) Its state on the transformer’s output acts because the picture illustration. 1D positional embeddings (1, 2, 3, 4,…, 9) are used to retain positional info.
The encoder consists of multi-head self-attention (MSA) and multi-layer perceptron (MLP) modules.
The usual qkv algorithm for self-attention is proven under. Q, Okay, and V stand for queries, keys, and values.
In MSA we carry out okay self-attention operations in parallel and concatenate their outputs.
Layernorm is utilized earlier than every block and residual connections after every block. MLP accommodates two layers with GELU activations.
The primary layer of the transformer linearly initiatives patches into embeddings. We are able to visualize the principal parts of the embedding filters.
These filters present foundation capabilities to signify the decrease dimensional constructions of the picture.
We are able to visualize the positional embeddings within the following method. Nearer embeddings are inclined to have related values.
In CNNs, decrease layers have a tendency to watch native info whereas last layers are inclined to seize world traits. Nonetheless, attributable to self-attention, transformers can seize world info even within the earliest phases. This may be noticed within the following graph. Decrease layers have consideration distances as much as 120 pixels.
Right here we practice a shallow imaginative and prescient transformer to categorise the MNIST photos. We divide the MNIST picture into 16 patches, flatten them and feed to the ViT.
A single head of consideration
class Head(nn.Module):
''' One head of self-attention '''
def __init__(self, head_size):
tremendous().__init__()
self.key = nn.Linear(n_embd, head_size, bias = False)
self.question = nn.Linear(n_embd, head_size, bias = False)
self.worth = nn.Linear(n_embd, head_size, bias = False)
self.dropout = nn.Dropout(dropout)
self.linear =def ahead(self, x):
B,T,C = x.form
okay = self.key(x)
q = self.question(x)
#compute consideration scores
wei = q @ okay.transpose(-2,-1) * C**(-0.5)
wei = F.softmax(wei, dim=-1)
wei = self.dropout(wei)
#carry out weighted aggregation of the values
v = self.worth(x)
out = wei @ v
return out
Multi-headed consideration
class MultiHeadAttention(nn.Module):
''' A number of heads of self-attention in parallel '''
def __init__(self, num_heads, head_size):
tremendous().__init__()
self.heads = nn.ModuleList([Head(head_size) for _ in range(num_heads)])
self.proj = nn.Linear(n_embd, n_embd)
self.dropout = nn.Dropout(dropout)def ahead(self, x):
out = torch.cat([h(x) for h in self.heads], dim=-1)
out = self.dropout(self.proj(out))
return out
Multilayer perceptron
class FeedForward(nn.Module):
'''A easy linear layer adopted by a non-linearity'''
def __init__(self, n_embd):
tremendous().__init__()
self.internet=nn.Sequential(
nn.Linear(n_embd, 4 * n_embd),
nn.ReLU(),
nn.Linear(4 * n_embd, n_embd),
nn.Dropout(dropout),
)def ahead(self,x):
return self.internet(x)
Encoder block
class Block(nn.Module):
def __init__(self,n_embd,n_head):
tremendous().__init__()
head_size = n_embd // n_head
self.sa = MultiHeadAttention(n_head,head_size)
self.ffwd = FeedForward(n_embd)
self.ln1 = nn.LayerNorm(n_embd)
self.ln2 = nn.LayerNorm(n_embd)def ahead(self,x):
x = x + self.sa(self.ln1(x))
x = x + self.ffwd(self.ln2(x))
return x
Imaginative and prescient-Transformer
class VisionTransformer(nn.Module):
def __init__(self, img_vec_size, n_embd, block_size=16):
tremendous().__init__()
self.encoder = nn.Linear(49, 32)
self.pos_embedding = nn.Linear(49, 32)
self.blocks = nn.Sequential(
Block(n_embd, n_head=4),
Block(n_embd, n_head=4),
Block(n_embd, n_head=4)
)
self.ln_f = nn.LayerNorm(n_embd)
self.vit_head = nn.Linear(n_embd, 10)def ahead(self, imgs):
patch_size = 7
imgs_patches = imgs.unfold(2, patch_size, patch_size).unfold(3, patch_size, patch_size)
imgs_patches = imgs_patches.contiguous().view(64, 16, 49)
x = self.encoder(imgs_patches)
x = x + self.pos_embedding(imgs_patches)
x = self.blocks(x)
x = self.ln_f(x)
x = self.vit_head(x)
x = x[:, 0] # Use first token for classification
x = torch.softmax(x, dim=1)
return x
The next code was used to coach the module.
# Load MNIST Dataset
remodel = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.5,), (0.5,))
])train_dataset = torchvision.datasets.MNIST(root='./information', practice=True, obtain=True, remodel=remodel)
train_loader = DataLoader(train_dataset, batch_size=64, shuffle=True, drop_last=True)
# Initialize the VisionTransformer mannequin
img_vec_size = 49 # 7x7 patch flattened
n_embd = 32 # Embedding dimension
gadget = torch.gadget('cuda' if torch.cuda.is_available() else 'cpu')
mannequin = VisionTransformer(img_vec_size, n_embd).to(gadget)
# Outline Loss and Optimizer
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(mannequin.parameters(), lr=3e-4)
# Initialize listing to trace accuracy for plotting
train_accuracies = []
losses = []
# Coaching loop for just a few epochs
num_epochs = 20
for epoch in vary(num_epochs):
mannequin.practice() # Set mannequin to coaching mode
running_loss = 0.0
appropriate = 0
complete = 0
for i, (photos, labels) in enumerate(train_loader, 1):
photos, labels = photos.to(gadget), labels.to(gadget)
# Ahead go
outputs = mannequin(photos)
# Calculate loss
loss = criterion(outputs, labels)
# Backward go
optimizer.zero_grad() # Zero the gradients
loss.backward() # Backpropagate the loss
# Replace weights
optimizer.step()
# Calculate accuracy for this batch
_, predicted = torch.max(outputs, 1)
complete += labels.measurement(0)
appropriate += (predicted == labels).sum().merchandise()
# Print loss each 100 batches
running_loss += loss.merchandise()
if i % 100 == 0:
avg_loss = running_loss / 100
#print(f"Epoch [{epoch+1}/{num_epochs}], Batch [{i}/{len(train_loader)}], Loss: {avg_loss:.4f}")
running_loss = 0.0
losses.append(avg_loss)
# Calculate epoch coaching accuracy
epoch_accuracy = 100 * appropriate / complete
train_accuracies.append(epoch_accuracy)
print(f"Epoch [{epoch+1}/{num_epochs}] Coaching Accuracy: {epoch_accuracy:.2f}%")
torch.save(mannequin.state_dict(), "vision_transformer.pth")
# Plot coaching accuracy
plt.plot(vary(1, num_epochs + 1), train_accuracies, marker='o', linestyle='-', shade='b')
plt.title('Coaching Accuracy over Epochs')
plt.xlabel('Epoch')
plt.ylabel('Accuracy (%)')
plt.present()
# Plot coaching loss
plt.plot(vary(1, len(losses) + 1), losses, marker='o', linestyle='-', shade='r')
plt.title('Coaching Loss over Epochs')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.present()
References
The mannequin reaches 94.6% practice accuracy.
Dosovitskiy, A., Beyer, L., Kolesnikov, A., Weissenborn, D., Zhai, X., Unterthiner, T., Dehghani, M., Minderer, M., Heigold, G., Gelly, S., Uszkoreit, J., & Houlsby, N. (2020). An Picture is Price 16×16 Phrases: Transformers for Picture Recognition at Scale. ArXiv. /abs/2010.11929
Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., Kaiser, L., & Polosukhin, I. (2017). Consideration Is All You Want. ArXiv. /abs/1706.03762
Devlin, J., Chang, M., Lee, Okay., & Toutanova, Okay. (2018). BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. ArXiv. /abs/1810.04805