mechanics is a method to describe how bodily methods, like planets or pendulums, transfer over time, specializing in power somewhat than simply forces. By reframing complicated dynamics by means of power lenses, this Nineteenth-century physics framework now powers cutting-edge generative AI. It makes use of generalized coordinates ( q ) (like place) and their conjugate momenta ( p ) (associated to momentum), forming a section house that captures the system’s state. This strategy is especially helpful for complicated methods with many components, making it simpler to search out patterns and conservation legal guidelines.
Desk of Contents
Mathematical Reformation: From Second-Order to First Order ⚙️
Newton’s ( F = mddot{q} ) requires fixing second-order differential equations, which turn into unwieldy for constrained methods or when figuring out conserved portions.
The Core Concept
Hamiltonian mechanics splits ( ddot{q} = F(q)/m ) into two first-order equations by introducing conjugate momentum ( p ):
[
begin{align*}
dot{q} = frac{partial H}{partial p} & text{(Position)}, quad dot{p} = -frac{partial H}{partial q} & text{(Momentum)}
end{align*}
]
It decomposes acceleration into complementary momentum/place flows. This section house perspective reveals hidden geometric construction.
Lagrangian Prelude: Motion Ideas
The Lagrangian ( mathcal{L}(q, dot{q}) = Ok – U ) results in Euler-Lagrange equations by way of variational calculus:
[
frac{d}{dt}left( frac{partial mathcal{L}}{partial dot{q}} right) – frac{partial mathcal{L}}{partial q} = 0
]
Kinetic Power Image
Observe that the ( Ok ) within the ( mathcal{L}(q, dot{q}) = Ok – U ) can also be represented as ( T ).
However these stay second-order. The important leap comes by means of Legendre Transformation ( (dot{q} rightarrow p) ). The Hamiltonian is derived from the Lagrangian by means of a Legendre transformation by defining the conjugate momentum as ( p_i = frac{partial mathcal{L}}{partial dot{q}_i} ); then the Hamiltonian will be written as:
[
H(q,p) = sum_i p_i dot{q}_i – mathcal{L}(q, dot{q})
]
We are able to write ( H(q,p) ) extra intuitively as:
[
H(q,p) = K(p) + U(q)
]
This flips the script: as a substitute of ( dot{q} )-centric dynamics, we get symplectic section circulate.
Why This Issues
The Hamiltonian turns into the system’s whole power ( H = Ok + U ) for a lot of bodily methods. It additionally supplies a framework the place time evolution is a canonical transformation – a symmetry preserving the elemental Poisson bracket construction ( {q_i, p_j} = delta_{ij} ).
For extra about canonical, non-canonical transformations, and Poisson bracket, together with detailed math and examples, try the TorchEBM post on Hamiltonian mechanics.
This transformation is just not canonical as a result of it doesn’t protect the Poisson bracket construction.
Newton vs. Lagrange vs. Hamilton: A Philosophical Showdown
| Facet | Newtonian | Lagrangian | Hamiltonian |
|---|---|---|---|
| State Variables | Place ( x ) and velocity ( dot{x} ) | Generalized coordinates ( q ) and velocities ( dot{q} ) | Generalized coordinates ( q ) and conjugate momenta ( p ) |
| Formulation | Second-order differential equations ( (F=ma) ) | Precept of least motion (( delta int L , dt = 0 )): ( L = Ok – U ) | First-order differential equations from Hamiltonian operate (Part circulate ( (dH) )): ( H = Ok + U ) |
| Figuring out Symmetries | Guide identification or by means of particular strategies | Noether’s theorem | Canonical transformations and Poisson brackets |
| Machine Studying Connection | Physics-informed neural networks, simulations | Optimum management, reinforcement studying | Hamiltonian Monte Carlo (HMC) sampling, energy-based fashions |
| Power Conservation | Not inherent (have to be derived) | Constructed-in by means of conservation legal guidelines | Central (Hamiltonian is power) |
| Normal Coordinates | Attainable, however usually cumbersome | Pure match | Pure match |
| Time Reversibility | Sure | Sure | Sure, particularly in symplectic formulations |
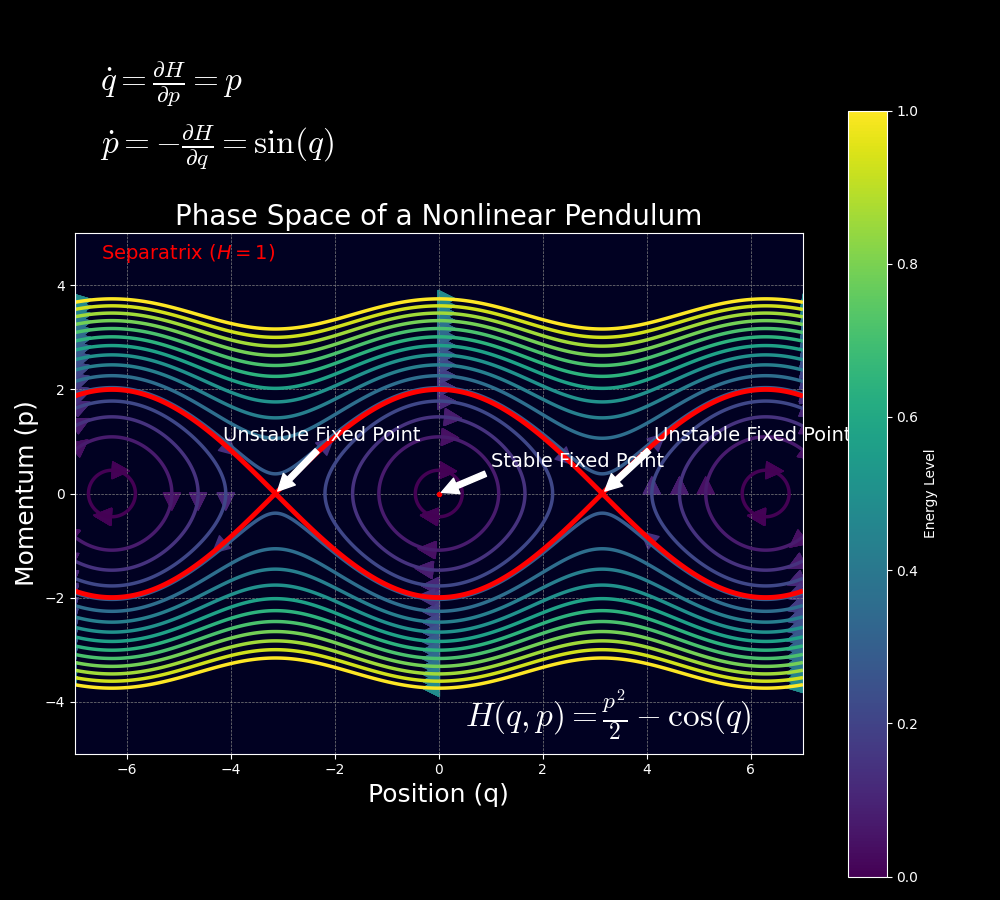
Hamilton’s Equations: The Geometry of Part Area ⚙️
The section house is a mathematical house the place we are able to characterize the set of doable states of a bodily system. For a system with ( n ) levels of freedom, the section house is a ( 2n )-dimensional house, usually visualized as a map the place every level ( (q, p) ) represents a novel state. The evolution of the system is described by the movement of a degree on this house, ruled by Hamilton’s equations.
This formulation gives a number of benefits. It makes it easy to establish conserved portions and symmetries by means of canonical transformations and Poisson brackets, which supplies deeper insights into the system’s conduct. As an illustration, Liouville’s theorem states that the amount in section house occupied by an ensemble of methods stays fixed over time, expressed as:
[
frac{partial rho}{partial t} + {rho, H} = 0
]
or equivalently:
[
frac{partial rho}{partial t} + sum_i left(frac{partial rho}{partial q_i}frac{partial H}{partial p_i} – frac{partial rho}{partial p_i}frac{partial H}{partial q_i}right) = 0
]
the place ( rho(q, p, t) ) is the density operate. This helps us to characterize the section house flows and the way they protect space below symplectic transformations. Its relation to symplectic geometry permits mathematical properties which might be immediately related to many numerical strategies. As an illustration, it permits hamiltonian monte carlo to carry out effectively in high-dimensions by defining MCMC methods that will increase the probabilities of accepting a pattern (particle).
Symplecticity: The Sacred Invariant
Hamiltonian flows protect the symplectic 2-form ( omega = sum_i dq_i wedge dp_i ).
Symplectic 2-form ( omega )
The symplectic 2-form, denoted by ( omega = sum_i dq_i wedge dp_i ), is a mathematical object utilized in symplectic geometry. It measures the world of parallelograms fashioned by vectors within the tangent house of a section house.
- ( dq_i ) and ( dp_i ): Infinitesimal modifications in place and momentum coordinates.
- ( wedge ): The wedge product, which mixes differential types in an antisymmetric approach that means that ( dq_i wedge dp_i = -dp_i wedge dq_i ).
- ( sum_i ): Sum over all levels of freedom.
Think about a section house the place every level represents a state of a bodily system. The symplectic kind assigns a price to every pair of vectors, successfully measuring the world of the parallelogram they span. This space is preserved below Hamiltonian flows.
Key Properties
- Closed: ( domega = 0 ) which suggests its exterior spinoff is zero ( domega=0 ). This property ensures that the shape doesn’t change below steady transformations.
- Non-degenerate: The shape is non-degenerate if ( domega(X,Y)=0 ) for all ( Y )s, then ( X=0 ). This ensures that each vector has a novel “companion” vector such that their pairing below ( omega ) is non-zero.
Instance
For a easy harmonic oscillator with one diploma of freedom, ( omega = dq wedge dp ). This measures the world of parallelograms within the section house spanned by vectors representing modifications in place and momentum.
A Very Simplistic PyTorch Code:
Whereas PyTorch doesn’t immediately deal with differential types, you possibly can conceptually characterize the symplectic kind utilizing tensors:
This code illustrates the antisymmetric nature of the wedge product.
Numerically, this implies good integrators should respect:
[
frac{partial (q(t + epsilon), p(t + epsilon))}{partial (q(t), p(t))}^T J frac{partial (q(t + epsilon), p(t + epsilon))}{partial (q(t), p(t))} = J text{where } J = begin{pmatrix} 0 & I -I & 0 end{pmatrix}
]
Breaking Down the Components
- Geometric numerical integration: Solves differential equations whereas preserving geometric properties of the system.
- Symplecticity: A geometrical property inherent to Hamiltonian methods. It ensures that the world of geometric constructions (e.g., parallelograms) in section house ( (q, p) ) stays fixed over time. That is encoded within the symplectic kind ( omega = sum_i dq_i wedge dp_i ).
- A numerical methodology is symplectic: If it preserves ( omega ). The Jacobian matrix of the transformation from ( (q(t), p(t)) ) to ( (q(t + epsilon), p(t + epsilon)) ) should fulfill the situation above.
- Jacobian matrix ( frac{partial (q(t + epsilon), p(t + epsilon))}{partial (q(t), p(t))} ): Quantifies how small modifications within the preliminary state ( (q(t), p(t)) ) propagate to the subsequent state ( (q(t + epsilon), p(t + epsilon)) ).
- ( q(t) ) and ( p(t) ): Place and momentum at time ( t ).
- ( q(t + epsilon) ) and ( p(t + epsilon) ): Up to date place and momentum after one time step ( epsilon ).
- ( frac{partial}{partial (q(t), p(t))} ): Partial derivatives with respect to the preliminary state.
How are We Going to Clear up it?
Numerical solvers for differential equations inevitably introduce errors that have an effect on answer accuracy. These errors manifest as deviations from the true trajectory in section house, significantly noticeable in energy-conserving methods just like the harmonic oscillator. The errors fall into two most important classes: native truncation error, arising from the approximation of steady derivatives with discrete steps (proportional to ( mathcal{O}(epsilon^n+1) ) the place ( epsilon ) is the step dimension and n will depend on the strategy); and world accumulation error, which compounds over integration time.
Ahead Euler Technique Fails at This!
Key Challenge: Power Drift from Non-Symplectic Updates
The ahead Euler methodology (FEM) violates the geometric construction of Hamiltonian methods, resulting in power drift in long-term simulations. Let’s dissect why.
For an in depth exploration of how strategies like Ahead Euler carry out in Hamiltonian methods and why they don’t protect symplecticity—together with mathematical breakdowns and sensible examples—try this submit on Hamiltonian mechanics from the TorchEBM library documentation.
To beat this, we flip to symplectic integrators—strategies that respect the underlying geometry of Hamiltonian methods, main us naturally to the Leapfrog Verlet methodology, a robust symplectic various. 🚀
Symplectic Numerical Integrators 💻
Leapfrog Verlet
For a separable Hamiltonian ( H(q,p) = Ok(p) + U(q) ), the place the corresponding likelihood distribution is given by:
[
P(q,p) = frac{1}{Z} e^{-U(q)} e^{-K(p)},
]
the Leapfrog Verlet integrator proceeds as follows:
[
begin{aligned}
p_{i}left(t + frac{epsilon}{2}right) &= p_{i}(t) – frac{epsilon}{2} frac{partial U}{partial q_{i}}(q(t))
q_{i}(t + epsilon) &= q_{i}(t) + epsilon frac{partial K}{partial p_{i}}left(pleft(t + frac{epsilon}{2}right)right)
p_{i}(t + epsilon) &= p_{i}left(t + frac{epsilon}{2}right) – frac{epsilon}{2} frac{partial U}{partial q_{i}}(q(t + epsilon))
end{aligned}
]
This Störmer-Verlet scheme preserves symplecticity precisely, with native error ( mathcal{O}(epsilon^3) ) and world error ( mathcal{O}(epsilon^2) ). You possibly can learn extra about numerical methods and analysis in Python here.
How Precisely?
Need to know precisely how the Leapfrog Verlet methodology ensures symplecticity with detailed equations and proofs? The TorchEBM library documentation on Leapfrog Verlet breaks it down step-by-step.
Why Symplecticity Issues
They’re the reversible neural nets of physics simulations!
Symplectic integrators like Leapfrog Verlet are important for long-term stability in Hamiltonian methods.
- Part house preservation: The quantity in ( (q, p) )-space is conserved precisely, avoiding synthetic power drift.
- Approximate power conservation: Whereas power ( H(q,p) ) is just not completely conserved (as a result of ( mathcal{O}(epsilon^2) ) error), it oscillates close to the true worth over exponentially lengthy timescales.
- Sensible relevance: This makes symplectic integrators indispensable in molecular dynamics and Hamiltonian Monte Carlo (HMC), the place correct sampling depends on steady trajectories.

Euler’s methodology (first-order) systematically injects power into the system, inflicting the attribute outward spiral seen within the plots. Modified Euler’s methodology (second-order) considerably reduces this power drift. Most significantly, symplectic integrators just like the Leapfrog methodology protect the geometric construction of Hamiltonian methods even with comparatively massive step sizes by sustaining section house quantity conservation. This structural preservation is why Leapfrog stays the popular methodology for long-time simulations in molecular dynamics and astronomy, the place power conservation is important regardless of the seen polygon-like discretization artifacts at massive step sizes.
Non-symplectic strategies (e.g., Euler-Maruyama) usually fail catastrophically in these settings.
| Integrator | Symplecticity | Order | Kind |
|---|---|---|---|
| Euler Technique | ❌ | 1 | Specific |
| Symplectically Euler | ✅ | 1 | Specific |
| Leapfrog (Verlet) | ✅ | 2 | Specific |
| Runge-Kutta 4 | ❌ | 4 | Specific |
| Forest-Ruth Integrator | ✅ | 4 | Specific |
| Yoshida Sixth-order | ✅ | 6 | Specific |
| Heun’s Technique (RK2) | ❌ | 2 | Specific |
| Third-order Runge-Kutta | ❌ | 3 | Specific |
| Implicit Midpoint Rule | ✅ | 2 | Implicit (fixing equations) |
| Fourth-order Adams-Bashforth | ❌ | 4 | Multi-step (specific) |
| Backward Euler Technique | ❌ | 1 | Implicit (fixing equations) |
For extra particulars on issues like native and world errors or what these integrators are finest fitted to, there’s a helpful write-up over at Hamiltonian mechanics: Why Symplecticity Matters that covers all of it.
Hamiltonian Monte Carlo
Hamiltonian Monte Carlo (HMC) is a Markov chain Monte Carlo (MCMC) methodology that leverages Hamiltonian dynamics to effectively pattern from complicated likelihood distributions, significantly in Bayesian statistics and Machine Learning.
From Part Area to Likelihood Area
HMC interprets goal distribution ( P(z) ) as a Boltzmann distribution:
[
P(z) = frac{1}{Z} e^{frac{-E(z)}{T}}
]
Substituting into this formulation, the Hamiltonian offers us a joint density:
[
P(q,p) = frac{1}{Z} e^{-U(q)} e^{-K(p)} text{where } U(q) = -log[p(q), p(q|D)]
]
the place ( p(q|D) ) is the probability of the given information ( D ) and T=1 and due to this fact eliminated. We estimate our posterior distribution utilizing the potential power ( U(q) ) since ( P(q,p) ) consists of two impartial likelihood distributions.
Increase with synthetic momentum ( p sim mathcal{N}(0,M) ), then simulate Hamiltonian dynamics to suggest new ( q’ ) primarily based on the distribution of the place variables ( U(q) ) which acts because the “potential power” of the goal distribution ( P(q) ), thereby creating valleys at high-probability areas.
For extra on HMC, try this explanation or this tutorial.
Bodily Methods: ( H(q,p) = U(q) + Ok(p) ) represents whole power
Sampling Methods: ( H(q,p) = -log P(q) + frac{1}{2}p^T M^{-1} p ) defines exploration dynamics
The kinetic power with the favored type of ( Ok(p) = frac{1}{2}p^T M^{-1} p ), usually Gaussian, injects momentum to traverse these landscapes. Crucially, the mass matrix ( M ) performs the function of a preconditioner – diagonal ( M ) adapts to parameter scales, whereas dense ( M ) can align with correlation construction. ( M ) is symmetric, optimistic particular and usually diagonal.
What’s Optimistic Particular?
Optimistic Particular: For any non-zero vector ( x ), the expression ( x^T M x ) is at all times optimistic. This ensures stability and effectivity.

affect the form of those types. The plots depict:
a) Optimistic Particular Kind: A bowl-shaped floor the place all eigenvalues are optimistic, indicating a minimal.
b) Damaging Particular Kind: An inverted bowl the place all eigenvalues are damaging, indicating a most.
c) Indefinite Kind: A saddle-shaped floor with each optimistic and damaging eigenvalues, indicating neither a most nor a minimal.
Every subplot contains the matrix ( M ) and the corresponding quadratic kind (Q(x) = x^T M x). Picture by the author.
[
x^T M x > 0
]
Kinetic Power Selections
- Gaussian (Commonplace HMC): ( Ok(p) = frac{1}{2}p^T M^{-1} p )
Yields Euclidean trajectories, environment friendly for average dimensions. - Relativistic (Riemannian HMC): ( Ok(p) = sqrt{p^T M^{-1} p + c^2} )
Limits most velocity, stopping divergences in ill-conditioned areas. - Adaptive (Surrogate Gradients): Study ( Ok(p) ) by way of neural networks to match goal geometry.
Key Instinct
The Hamiltonian ( H(q,p) = U(q) + frac{1}{2}p^T M^{-1} p ) creates an power panorama the place momentum carries the sampler by means of high-probability areas, avoiding random stroll conduct.
The HMC Algorithm
The algorithm entails:
- Initialization: Begin with an preliminary place ( q_0 ) and pattern momentum ( p_0 sim mathcal{N}(0,M) ).
- Leapfrog Integration: Use the leapfrog methodology to approximate Hamiltonian dynamics. For a step dimension ( epsilon ) and L steps, replace:
- Half-step momentum: ( p(t + frac{epsilon}{2}) = p(t) – frac{epsilon}{2} frac{partial U}{partial q}(q(t)) )
- Full-step place: ( q(t + epsilon) = q(t) + epsilon frac{partial Ok}{partial p}(p(t + frac{epsilon}{2})) ), the place ( Ok(p) = frac{1}{2} p^T M^{-1} p ), so ( frac{partial Ok}{partial p} = M^{-1} p )
- Full-step momentum: ( p(t + epsilon) = p(t + frac{epsilon}{2}) – frac{epsilon}{2} frac{partial U}{partial q}(q(t + epsilon)) )
That is repeated L instances to get proposed ( dot{q} ) and ( dot{p} ).
- Metropolis-Hastings Acceptance: Settle for the proposed ( dot{q} ) with likelihood ( min(1, e^{H(q_0,p_0) – H(dot{q},dot{p})}) ), the place ( H(q,p) = U(q) + Ok(p) ).
This course of generates a Markov chain with stationary distribution ( P(q) ), leveraging Hamiltonian dynamics to take bigger, extra environment friendly steps in comparison with random-walk strategies.
Why Higher Than Random Stroll?
HMC navigates high-dimensional areas alongside power contours – like following mountain paths as a substitute of wandering randomly!
Recap of the Hamilton’s equations?
[
begin{cases}
dot{q} = nabla_p K(p) = M^{-1}p & text{(Guided exploration)}
dot{p} = -nabla_q U(q) = nabla_q log P(q) & text{(Bayesian updating)}
end{cases}
]
This coupled system drives ( (q,p) ) alongside iso-probability contours of ( P(q) ), with momentum rotating somewhat than resetting at every step like in Random Stroll Metropolis–consider following mountain paths as a substitute of wandering randomly! The important thing parameters – integration time ( tau = Lepsilon ) and step dimension ( epsilon ) – steadiness exploration vs. computational value:
- Brief ( tau ): Native exploration, increased acceptance
- Lengthy ( tau ): World strikes, threat of U-turns (periodic orbits)
Key Parameters and Tuning
Tuning ( M ) to match the covariance of ( P(q) ) (e.g., by way of warmup adaptation) and setting ( tau sim mathcal{O}(1/lambda_{textual content{max}}) ), the place ( lambda_{textual content{max}} ) is the biggest eigenvalue of ( nabla^2 U ), usually yields optimum mixing.
TorchEBM Library 📚
Oh, by the way in which, I’ve been messing round with these items in Python and threw collectively a library known as TorchEBM. It’s bought some instruments for energy-based, rating matching, diffusion- and flow-based fashions and HMC bits I’ve been enjoying with. Nothing fancy, only a researcher’s sandbox for testing concepts like these. Should you’re into coding this type of factor, poke round on TorchEBM GitHub and lemme know what you assume—PRs welcome! Been enjoyable tinkering with it whereas scripting this submit.
Reference to Power-Primarily based Fashions
Power-based fashions (EBMs) are a category of generative fashions that outline a likelihood distribution over information factors utilizing an power operate. The likelihood of an information level is proportional to ( e^{-E(x)} ), the place ( E(x) ) is the power operate. This formulation is immediately analogous to the Boltzmann distribution in statistical physics, the place the likelihood is expounded to the power of a state. In Hamiltonian mechanics, the Hamiltonian operate ( H(q, p) ) represents the entire power of the system, and the likelihood distribution in section house is given by ( e^{-H(q,p)/T} ), the place ( T ) is the temperature.
In EBMs, Hamiltonian Monte Carlo (HMC) is commonly used to pattern from the mannequin’s distribution. HMC leverages Hamiltonian dynamics to suggest new states, that are then accepted or rejected primarily based on the Metropolis-Hastings criterion. This methodology is especially efficient for high-dimensional issues, because it reduces the correlation between samples and permits for extra environment friendly exploration of the state house. As an illustration, in picture technology duties, HMC can pattern from the distribution outlined by the power operate, facilitating the technology of high-quality pictures.
EBMs outline likelihood by means of Hamiltonians:
[
p(x) = frac{1}{Z}e^{-E(x)} quad leftrightarrow quad H(q,p) = E(q) + K(p)
]
Potential Analysis Instructions 🔮
Symplecticity in Machine Studying Fashions

Incorporate the symplectic construction of Hamiltonian mechanics into machine studying fashions to protect properties like power conservation, which is essential for long-term predictions. Generalizing Hamiltonian Neural Networks (HNNs), as mentioned in Hamiltonian Neural Networks, to extra complicated methods or creating new architectures that protect symplecticity
HMC for Advanced Distributions
HMC for sampling from complicated, high-dimensional, and multimodal distributions, resembling these encountered in deep studying. Combining HMC with different strategies, like parallel tempering, may deal with distributions with a number of modes extra successfully.
Combining Hamiltonian Mechanics with Different ML Strategies
Combine Hamiltonian mechanics with reinforcement studying to information exploration in steady state and motion areas. Utilizing it to mannequin the atmosphere may enhance exploration methods, as seen in potential functions in robotics. Moreover, utilizing Hamiltonian mechanics to outline approximate posteriors in variational inference may result in extra versatile and correct approximations.
Hamiltonian GANs
Using Hamiltonian formalism as an inductive bias for the technology of bodily believable movies with neural networks.
Wanna Workforce Up on This? 🤓
If a few of you good people wherever you’re doing high-level wizardry are into analysis collaboration, I’d love to talk generative fashions over espresso ☕️ (digital or IRL (London)). Should you’re into pushing these concepts additional, hit me up! Observe me on Twitter/BlueSky or GitHub—I’m often rambling about these items there. Additionally on LinkedIn and Medium/TDS in the event you’re curious. To search out extra about my analysis pursuits, try my personal website.
Conclusion
Hamiltonian mechanics reframes bodily methods by means of power, utilizing section house to disclose symmetries and conservation legal guidelines by way of first-order equations. Symplectic integrators like Leapfrog Verlet protect this construction, making certain stability in simulations—essential for functions like molecular dynamics and Hamiltonian Monte Carlo (HMC). HMC leverages these dynamics to pattern complicated distributions effectively, bridging classical physics with trendy machine studying.
References and Helpful Hyperlinks 📚
[]