例子:
數據(參數):如上圖表,數據為工資(X1)以及年齡(X2)
目標(標籤):目標為額度(Y)
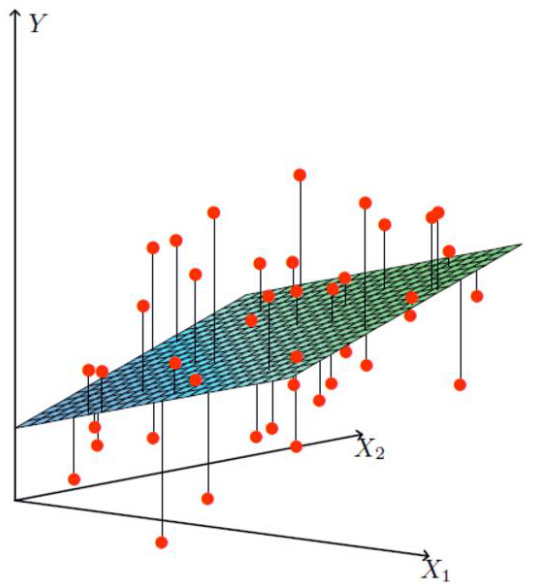
我們要依據數據,預測目標,可以簡單把上面的圖表轉成下圖,紅色點代表X1和X2的數據,中間的平面表示我們要找到一個線性方程,能夠擬合所有數據點,並且使誤差最小
用數學表達,假設θ1是年齡的參數,θ2是工資的參數,則這個平面的方程可以表示為
θ0為偏置項,可以簡單理解為上圖平面的上下平移,為了更有效率表示多維特徵的加總,我們將所有參數與輸入包裝成向量:
參數向量:
輸入向量(注意這裡故意在最前面加上 1,以配合偏置項):
將這兩個向量做點積(dot product),就會變成:
對於每個數據點來說,可以表達為
y(i) 表示真實值,即每個數據點i的y維度的值,也就是我們要預測的目標,為該數據經過擬合方程後得出預測值,再加上誤差值ε,對於單一數據點來說,理想狀態ε為0。
但是這在現實世界中是不可能的,大部分的擬合方程得出的預測值不可能完全沒有誤差,但對於好的擬合方程來說,對於所有數據點的誤差值趨近於真實值。
線性回歸使用最小二乘法(Least Squares Technique)來尋找最佳擬合線。其目標是最小化所有實際觀測值與預測值之間差的平方和,即最小化殘差平方和(Residual Sum of Squares, RSS)或稱為目標函數或是損失函數:
機器學習中比較常用的方法是均方誤差(Imply Squared Error, MSE),即最小二乘法再除以樣本數m:
y(i) 表示真實值,hθ(x(i))表示預測值,平方是為了消掉誤差的正負值避免正負值相加導致低估誤差
向量化公式:
其中:
- X:包含所有輸入資料的矩陣,形狀是 m×n每列是 [1,x1,x2]
- y:實際的輸出向量(額度)
- θ:我們要求解的參數向量
有目標函數J(θ)後,要如何求解?
如果只有一個變數,則稱為簡單線性回歸,可以用正規方程來解,假設有資料集 {(x1,y1),(x2,y2),…,(xn,yn)},可以利用微積分來最小化MSE。對θ1 和 θ0 分別取偏導並令其為 0,得到封閉解(Closed-form answer):
若資料集非常大或是多元線性回歸(多個變數),可以使用梯度下降法(Gradient Descent)來迭代逼近最小損失,目標函數如下(其實就是MSE,只是除以m改成除以2m,為了方便求導):
分別對 θ0和 θ1求偏導數後,得到每次更新的公式如下更新規則如下:
- α:學習率(studying price),表示每次更新的步長
- m:訓練樣本數
- x(i):第 i 筆輸入樣本
- y(i):第 i 筆標籤(實際值)
- hθ(x(i)):模型的預測值
如果寫成通用形式,更新的公式如下:
θ:模型參數向量(如 θ0,θ1)
∇θJ(θ):對 θ的偏微分,也就是「梯度」
梯度下降有三種形式,分別是批量梯度下降、隨機梯度下降、小批量梯度下降: