Clustering Eating Behaviors in Time: A Machine Learning Approach to Preventive Health

It’s nicely that what we eat issues — however what if when and how usually we eat issues simply as a lot?

Within the midst of ongoing scientific debate round the advantages of intermittent fasting, this query turns into much more intriguing. As somebody obsessed with machine studying and wholesome dwelling, I used to be impressed by a 2017 analysis paper[1] exploring this intersection. The authors launched a novel distance metric known as Modified Dynamic Time Warping (MDTW) — a method designed to account not just for the dietary content material of meals but in addition their timing all through the day.

Motivated by their work[1], I constructed a full implementation of MDTW from scratch utilizing Python. I utilized it to cluster simulated people into temporal dietary patterns, uncovering distinct behaviors like skippers, snackers, and evening eaters.

Whereas MDTW might sound like a distinct segment metric, it fills a essential hole in time-series comparability. Conventional distance measures — comparable to Euclidean distance and even classical Dynamic Time Warping (DTW) — wrestle when utilized to dietary information. Individuals don’t eat at mounted instances or with constant frequency. They skip meals, snack irregularly, or eat late at evening.

MDTW is designed for precisely this sort of temporal misalignment and behavioral variability. By permitting versatile alignment whereas penalizing mismatches in each nutrient content material and meal timing, MDTW reveals delicate however significant variations in how folks eat.

What this text covers:

1. Mathematical basis of MDTW — defined intuitively.
2. From formulation to code — implementing MDTW in Python with dynamic programming.
3. Producing artificial dietary information to simulate real-world consuming habits.
4. Constructing a distance matrix between particular person consuming information.
5. Clustering people with Ok-Medoids and evaluating with silhouette and elbow strategies.
6. Visualizing clusters as scatter plots and joint distributions.
7. Deciphering temporal patterns from clusters: who eats when and the way a lot?

Fast Be aware on Classical Dynamic Time Warping (DTW)

Dynamic Time Warping (DTW) is a traditional algorithm used to measure similarity between two sequences which will fluctuate in size or timing. It’s extensively utilized in speech recognition, gesture evaluation, and time collection alignment. Let’s see a quite simple instance of the Sequence A is aligned to Sequence B (shifted model of B) with utilizing conventional dynamic time warping algorithm utilizing fastdtw library. As enter, we give a distance metric as Euclidean. Additionally, we put time collection to calculate the gap between these time collection and optimized aligned path.

import numpy as np
import matplotlib.pyplot as plt
from fastdtw import fastdtw
from scipy.spatial.distance import euclidean
# Pattern sequences (scalar values)
x = np.linspace(0, 3 * np.pi, 30)
y1 = np.sin(x)
y2 = np.sin(x+0.5)  # Shifted model
# Convert scalars to vectors (1D)
y1_vectors = [[v] for v in y1]
y2_vectors = [[v] for v in y2]
# Use absolute distance for scalars
distance, path = fastdtw(y1_vectors, y2_vectors, dist=euclidean)
#or for scalar 
# distance, path = fastdtw(y1, y2, dist=lambda x, y: np.abs(x-y))

distance, path = fastdtw(y1, y2,dist=lambda x, y: np.abs(x-y))
# Plot the alignment
plt.determine(figsize=(10, 4))
plt.plot(y1, label='Sequence A (gradual)')
plt.plot(y2, label='Sequence B (shifted)')

# Draw alignment strains
for (i, j) in path:
    plt.plot([i, j], [y1[i], y2[j]], shade='grey', linewidth=0.5)

plt.title(f'Dynamic Time Warping Alignment (Distance = {distance:.2f})')
plt.xlabel('Time Index')
plt.legend()
plt.tight_layout()
plt.savefig('dtw_alignment.png')
plt.present()

The trail returned by fastdtw (or any DTW algorithm) is a sequence of index pairs (i, j) that symbolize the optimum alignment between two time collection. Every pair signifies that aspect A[i] is matched with B[j]. By summing the distances between all these matched pairs, the algorithm computes the optimized cumulative value — the minimal complete distance required to warp one sequence to the opposite.

Modified Dynamic Warping

The important thing problem when making use of dynamic time warping (DTW) to dietary information (vs. easy examples like sine waves or fixed-length sequences) lies within the complexity and variability of real-world consuming behaviors. Some challenges and the proposed resolution within the paper[1] as a response to every problem are as follows:

1. Irregular Time Steps: MDTW accounts for this by explicitly incorporating the time distinction within the distance operate.
2. Multidimensional Vitamins: MDTW helps multidimensional vectors to symbolize vitamins comparable to energy, fats and so on. and makes use of a weight matrix to deal with differing models and the significance of vitamins,
3. Unequal variety of meals: MDTW permits for matching with empty consuming occasions, penalizing skipped or unmatched meals appropriately.
4. Time Sensitivity: MDTW contains a time distinction penalty, weighting consuming occasions far aside in time even when the vitamins are related.

Consuming Event Information Illustration

In accordance with the modified dynamic time warping proposed within the paper[1], every individual’s food plan will be regarded as a sequence of consuming occasions, the place every occasion has:

As an example how consuming information seem in actual information, I created three artificial dietary profiles solely contemplating calorie consumption — Skipper, Night time Eater, and Snacker. Let’s assume if we ingest the uncooked information from an API on this format:

skipper={
    'person_id': 'skipper_1',
    'information': [
        {'time': 12, 'nutrients': [300]},  # Skipped breakfast, giant lunch
        {'time': 19, 'vitamins': [600]},  # Massive dinner
    ]
}
night_eater={
    'person_id': 'night_eater_1',
    'information': [
        {'time': 9, 'nutrients': [150]},   # Gentle breakfast
        {'time': 14, 'vitamins': [250]},  # Small lunch
        {'time': 22, 'vitamins': [700]},  # Massive late dinner
    ]
}
snacker=  {
    'person_id': 'snacker_1',
    'information': [
        {'time': 8, 'nutrients': [100]},   # Gentle morning snack
        {'time': 11, 'vitamins': [150]},  # Late morning snack
        {'time': 14, 'vitamins': [200]},  # Afternoon snack
        {'time': 17, 'vitamins': [100]},  # Early night snack
        {'time': 21, 'vitamins': [200]},  # Night time snack
    ]
}
raw_data = [skipper, night_eater, snacker]

As instructed within the paper, the dietary values ought to be normalized by the entire calorie consumptions.

import numpy as np
import matplotlib.pyplot as plt
def create_time_series_plot(information,save_path=None):
    plt.determine(figsize=(10, 5))
    for individual,file in information.gadgets():
        #in case the nutrient vector has multiple dimension
        information=[[time, float(np.mean(np.array(value)))] for time,worth in file.gadgets()]

        time = [item[0] for merchandise in information]
        nutrient_values = [item[1] for merchandise in information]
        # Plot the time collection
        plt.plot(time, nutrient_values, label=individual, marker='o')

    plt.title('Time Sequence Plot for Nutrient Information')
    plt.xlabel('Time')
    plt.ylabel('Normalized Nutrient Worth')
    plt.legend()
    plt.grid(True)
    if save_path:
        plt.savefig(save_path)

def prepare_person(individual):
    
    # Test if all vitamins have similar size
    nutrients_lengths = [len(record['nutrients']) for file in individual["records"]]
    
    if len(set(nutrients_lengths)) != 1:
        increase ValueError(f"Inconsistent nutrient vector lengths for individual {individual['person_id']}.")

    sorted_records = sorted(individual["records"], key=lambda x: x['time'])

    vitamins = np.stack([np.array(record['nutrients']) for file in sorted_records])
    total_nutrients = np.sum(vitamins, axis=0)

    # Test to keep away from division by zero
    if np.any(total_nutrients == 0):
        increase ValueError(f"Zero complete vitamins for individual {individual['person_id']}.")

    normalized_nutrients = vitamins / total_nutrients

    # Return a dictionary {time: [normalized nutrients]}
    person_dict = {
        file['time']: normalized_nutrients[i].tolist()
        for i, file in enumerate(sorted_records)
    }

    return person_dict
prepared_data = {individual['person_id']: prepare_person(individual) for individual in raw_data}
create_time_series_plot(prepared_data)

Calculation Distance of Pairs

The computation of distance measure between pair of people are outlined within the formulation beneath. The primary time period symbolize an Euclidean distance of nutrient vectors whereas the second takes into consideration the time penalty.

This formulation is carried out within the local_distance operate with the instructed values:

import numpy as np

def local_distance(eo_i, eo_j,delta=23, beta=1, alpha=2):
    """
    Calculate the native distance between two occasions.
    Args:
        eo_i (tuple): Occasion i (time, vitamins).
        eo_j (tuple): Occasion j (time, vitamins).
        delta (float): Time scaling issue.
        beta (float): Weighting issue for time distinction.
        alpha (float): Exponent for time distinction scaling.
    Returns:
        float: Native distance.
    """
    ti, vi = eo_i
    tj, vj = eo_j
   
    vi = np.array(vi)
    vj = np.array(vj)

    if vi.form != vj.form:
        increase ValueError("Mismatch in characteristic dimensions.")
    if np.any(vi < 0) or np.any(vj < 0):
        increase ValueError("Nutrient values should be non-negative.")
    if np.any(vi>1 ) or np.any(vj>1):
        increase ValueError("Nutrient values should be within the vary [0, 1].")   
    W = np.eye(len(vi))  # Assume W = identification for now
    value_diff = (vi - vj).T @ W @ (vi - vj) 
    time_diff = (np.abs(ti - tj) / delta) ** alpha
    scale = 2 * beta * (vi.T @ W @ vj)
    distance = value_diff + scale * time_diff
  
    return distance

We assemble an area distance matrix deo(i,j) for every pair of people being in contrast. The variety of rows and columns on this matrix corresponds to the variety of consuming events for every particular person.

As soon as the native distance matrix deo(i,j) is constructed — capturing the pairwise distances between all consuming events of two people — the subsequent step is to compute the world value matrix dER(i,j). This matrix accumulates the minimal alignment value by contemplating three doable transitions at every step: matching two consuming events, skipping an event within the first file (aligning to an empty), or skipping an event within the second file.

To compute the total distance between two sequences of consuming events, we construct:

A native distance matrix deo crammed utilizing local_distance.

• A world value matrix dER utilizing dynamic programming, minimizing over:
• Match
• Skip within the first sequence (align to empty)
• Skip within the second sequence

These straight implement the recurrence:

import numpy as np

def mdtw_distance(ER1, ER2, delta=23, beta=1, alpha=2):
    """
    Calculate the modified DTW distance between two sequences of occasions.
    Args:
        ER1 (record): First sequence of occasions (time, vitamins).
        ER2 (record): Second sequence of occasions (time, vitamins).
        delta (float): Time scaling issue.
        beta (float): Weighting issue for time distinction.
        alpha (float): Exponent for time distinction scaling.
    
    Returns:
        float: Modified DTW distance.
    """
    m1 = len(ER1)
    m2 = len(ER2)
   
    # Native distance matrix together with matching with empty
    deo = np.zeros((m1 + 1, m2 + 1))

    for i in vary(m1 + 1):
        for j in vary(m2 + 1):
            if i == 0 and j == 0:
                deo[i, j] = 0
            elif i == 0:
                tj, vj = ER2[j-1]
                deo[i, j] = np.dot(vj, vj)  
            elif j == 0:
                ti, vi = ER1[i-1]
                deo[i, j] = np.dot(vi, vi)
            else:
                deo[i, j]=local_distance(ER1[i-1], ER2[j-1], delta, beta, alpha)

    # # World value matrix
    dER = np.zeros((m1 + 1, m2 + 1))
    dER[0, 0] = 0

    for i in vary(1, m1 + 1):
        dER[i, 0] = dER[i-1, 0] + deo[i, 0]
    for j in vary(1, m2 + 1):
        dER[0, j] = dER[0, j-1] + deo[0, j]

    for i in vary(1, m1 + 1):
        for j in vary(1, m2 + 1):
            dER[i, j] = min(
                dER[i-1, j-1] + deo[i, j],   # Match i and j
                dER[i-1, j] + deo[i, 0],     # Match i to empty
                dER[i, j-1] + deo[0, j]      # Match j to empty
            )
   
    
    return dER[m1, m2]  # Return the ultimate value

ERA = record(prepared_data['skipper_1'].gadgets())
ERB = record(prepared_data['night_eater_1'].gadgets())
distance = mdtw_distance(ERA, ERB)
print(f"Distance between skipper_1 and night_eater_1: {distance}")

From Pairwise Comparisons to a Distance Matrix

As soon as we outline find out how to calculate the gap between two people’ consuming patterns utilizing MDTW, the subsequent pure step is to compute distances throughout the complete dataset. To do that, we assemble a distance matrix the place every entry (i,j) represents the MDTW distance between individual i and individual j.

That is carried out within the operate beneath:

import numpy as np

def calculate_distance_matrix(prepared_data):
    """
    Calculate the gap matrix for the ready information.
    
    Args:
        prepared_data (dict): Dictionary containing ready information for every individual.
        
    Returns:
        np.ndarray: Distance matrix.
    """
    n = len(prepared_data)
    distance_matrix = np.zeros((n, n))
    
    # Compute pairwise distances
    for i, (id1, records1) in enumerate(prepared_data.gadgets()):
        for j, (id2, records2) in enumerate(prepared_data.gadgets()):
            if i < j:  # Solely higher triangle
                print(f"Calculating distance between {id1} and {id2}")
                ER1 = record(records1.gadgets())
                ER2 = record(records2.gadgets())
                
                distance_matrix[i, j] = mdtw_distance(ER1, ER2)
                distance_matrix[j, i] = distance_matrix[i, j]  # Symmetric matrix
                
    return distance_matrix
def plot_heatmap(matrix,people_ids,save_path=None):
    """
    Plot a heatmap of the gap matrix.  
    Args:
        matrix (np.ndarray): The space matrix.
        title (str): The title of the plot.
        save_path (str): Path to save lots of the plot. If None, the plot is not going to be saved.
    """
    plt.determine(figsize=(8, 6))
    plt.imshow(matrix, cmap='sizzling', interpolation='nearest')
    plt.colorbar()
  
    plt.xticks(ticks=vary(len(matrix)), labels=people_ids)
    plt.yticks(ticks=vary(len(matrix)), labels=people_ids)
    plt.xticks(rotation=45)
    plt.yticks(rotation=45)
    if save_path:
        plt.savefig(save_path)
    plt.title('Distance Matrix Heatmap')

distance_matrix = calculate_distance_matrix(prepared_data)
plot_heatmap(distance_matrix, record(prepared_data.keys()), save_path='distance_matrix.png')

After computing the pairwise Modified Dynamic Time Warping (MDTW) distances, we are able to visualize the similarities and variations between people’ dietary patterns utilizing a heatmap. Every cell (i,j) within the matrix represents the MDTW distance between individual i and individual j— decrease values point out extra related temporal consuming profiles.

This heatmap affords a compact and interpretable view of dietary dissimilarities, making it simpler to establish clusters of comparable consuming behaviors.

This means that skipper_1 shares extra similarity with night_eater_1 than with snacker_1. The reason being that each skipper and evening eater have fewer, bigger meals concentrated later within the day, whereas the snacker distributes smaller meals extra evenly throughout the complete timeline.

Clustering Temporal Dietary Patterns

After calculating the pairwise distances utilizing Modified Dynamic Time Warping (MDTW), we’re left with a distance matrix that displays how dissimilar every particular person’s consuming sample is from the others. However this matrix alone doesn’t inform us a lot at a look — to disclose construction within the information, we have to go one step additional.

Earlier than making use of any Clustering Algorithm, we first want a dataset that displays lifelike dietary behaviors. Since entry to large-scale dietary consumption datasets will be restricted or topic to utilization restrictions, I generated artificial consuming occasion information that simulate numerous each day patterns. Every file represents an individual’s calorie consumption at particular hours all through a 24-hour interval.

import numpy as np

def generate_synthetic_data(num_people=5, min_meals=1, max_meals=5,min_calories=200,max_calories=800):
    """
    Generate artificial information for a given variety of folks.
    Args:
        num_people (int): Variety of folks to generate information for.
        min_meals (int): Minimal variety of meals per individual.
        max_meals (int): Most variety of meals per individual.
        min_calories (int): Minimal energy per meal.
        max_calories (int): Most energy per meal.
    Returns:
        record: Listing of dictionaries containing artificial information for every individual.
    """
    information = []
    np.random.seed(42)  # For reproducibility
    for person_id in vary(1, num_people + 1):
        num_meals = np.random.randint(min_meals, max_meals + 1)  # random variety of meals between min and max
        meal_times = np.type(np.random.selection(vary(24), num_meals, exchange=False))  # random instances sorted

        raw_calories = np.random.randint(min_calories, max_calories, measurement=num_meals)  # random energy between min and max

        person_record = {
            'person_id': f'person_{person_id}',
            'information': [
                {'time': float(time), 'nutrients': [float(cal)]} for time, cal in zip(meal_times, raw_calories)
            ]
        }

        information.append(person_record)
    return information

raw_data=generate_synthetic_data(num_people=1000, min_meals=1, max_meals=5,min_calories=200,max_calories=800)
prepared_data = {individual['person_id']: prepare_person(individual) for individual in raw_data}
distance_matrix = calculate_distance_matrix(prepared_data)

Selecting the Optimum Variety of Clusters

To find out the suitable variety of clusters for grouping dietary patterns, I evaluated two common strategies: the Elbow Technique and the Silhouette Rating.

• The Elbow Technique analyzes the clustering value (inertia) because the variety of clusters will increase. As proven within the plot, the price decreases sharply as much as 4 clusters, after which the speed of enchancment slows considerably. This “elbow” suggests diminishing returns past 4 clusters.
• The Silhouette Rating, which measures how nicely every object lies inside its cluster, confirmed a comparatively excessive rating at 4 clusters (≈0.50), even when it wasn’t absolutely the peak.

The next code computes the clustering value and silhouette scores for various values of okay (variety of clusters), utilizing the Ok-Medoids algorithm and a precomputed distance matrix derived from the MDTW metric:

from sklearn.metrics import silhouette_score
from sklearn_extra.cluster import KMedoids
import matplotlib.pyplot as plt

prices = []
silhouette_scores = []
for okay in vary(2, 10):
    mannequin = KMedoids(n_clusters=okay, metric='precomputed', random_state=42)
    labels = mannequin.fit_predict(distance_matrix)
    prices.append(mannequin.inertia_)
    rating = silhouette_score(distance_matrix, mannequin.labels_, metric='precomputed')
    silhouette_scores.append(rating)

# Plot
ks = record(vary(2, 10))
fig, ax1 = plt.subplots(figsize=(8, 5))

color1 = 'tab:blue'
ax1.set_xlabel('Variety of Clusters (okay)')
ax1.set_ylabel('Price (Inertia)', shade=color1)
ax1.plot(ks, prices, marker='o', shade=color1, label='Price')
ax1.tick_params(axis='y', labelcolor=color1)

# Create a second y-axis that shares the identical x-axis
ax2 = ax1.twinx()
color2 = 'tab:crimson'
ax2.set_ylabel('Silhouette Rating', shade=color2)
ax2.plot(ks, silhouette_scores, marker='s', shade=color2, label='Silhouette Rating')
ax2.tick_params(axis='y', labelcolor=color2)

# Non-compulsory: mix legends
lines1, labels1 = ax1.get_legend_handles_labels()
lines2, labels2 = ax2.get_legend_handles_labels()
ax1.legend(lines1 + lines2, labels1 + labels2, loc='higher proper')
ax1.vlines(x=4, ymin=min(prices), ymax=max(prices), shade='grey', linestyle='--', linewidth=0.5)

plt.title('Price and Silhouette Rating vs Variety of Clusters')
plt.tight_layout()
plt.savefig('clustering_metrics_comparison.png')
plt.present()

Deciphering the Clustered Dietary Patterns

As soon as the optimum variety of clusters (okay=4) was decided, every particular person within the dataset was assigned to one among these clusters utilizing the Ok-Medoids mannequin. Now, we have to perceive what characterizes every cluster.

To take action, I adopted the strategy instructed within the unique MDTW paper [1]: analyzing the largest consuming event for each particular person, outlined by each the time of day it occurred and the fraction of complete each day consumption it represented. This offers perception into when folks eat essentially the most energy and how a lot they eat throughout that peak event.

# Kmedoids clustering with the optimum variety of clusters
from sklearn_extra.cluster import KMedoids
import seaborn as sns
import pandas as pd

okay=4
mannequin = KMedoids(n_clusters=okay, metric='precomputed', random_state=42)
labels = mannequin.fit_predict(distance_matrix)

# Discover the time and fraction of their largest consuming event
def get_largest_event(file):
    complete = sum(v[0] for v in file.values())
    largest_time, largest_value = max(file.gadgets(), key=lambda x: x[1][0])
    fractional_value = largest_value[0] / complete if complete > 0 else 0
    return largest_time, fractional_value

# Create a largest meal information per cluster
data_per_cluster = {i: [] for i in vary(okay)}
for i, person_id in enumerate(prepared_data.keys()):
    cluster_id = labels[i]
    t, v = get_largest_event(prepared_data[person_id])
    data_per_cluster[cluster_id].append((t, v))

import seaborn as sns
import matplotlib.pyplot as plt
import pandas as pd

# Convert to pandas DataFrame
rows = []
for cluster_id, values in data_per_cluster.gadgets():
    for hour, fraction in values:
        rows.append({"Hour": hour, "Fraction": fraction, "Cluster": f"Cluster {cluster_id}"})
df = pd.DataFrame(rows)
plt.determine(figsize=(10, 6))
sns.scatterplot(information=df, x="Hour", y="Fraction", hue="Cluster", palette="tab10")
plt.title("Consuming Occasions Throughout Clusters")
plt.xlabel("Hour of Day")
plt.ylabel("Fraction of Day by day Consumption (largest meal)")
plt.grid(True)
plt.tight_layout()
plt.present()

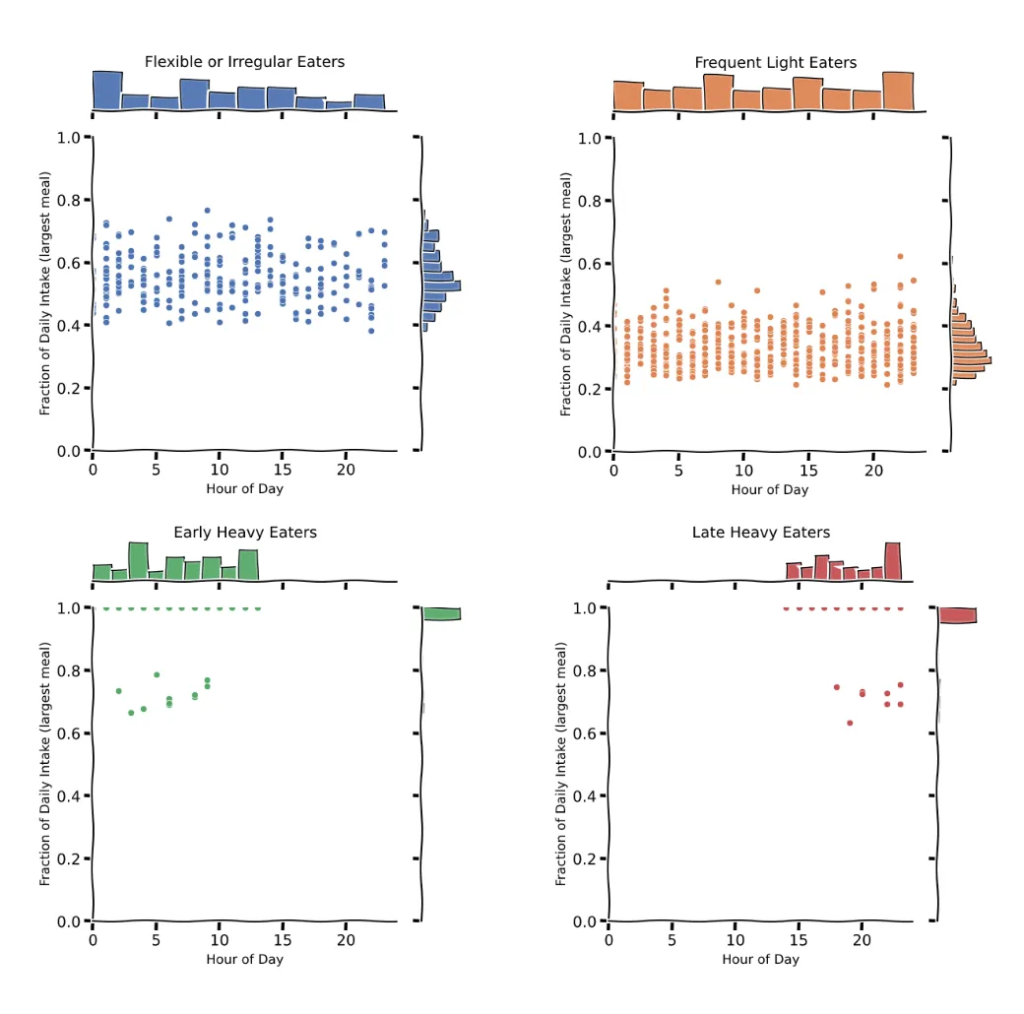
Whereas the scatter plot affords a broad overview, a extra detailed understanding of every cluster’s consuming habits will be gained by inspecting their joint distributions.
By plotting the joint histogram of the hour and fraction of each day consumption for the biggest meal, we are able to establish attribute patterns, utilizing the code beneath:

# Plot every cluster utilizing seaborn.jointplot
for cluster_label in df['Cluster'].distinctive():
    cluster_data = df[df['Cluster'] == cluster_label]
    g = sns.jointplot(
        information=cluster_data,
        x="Hour",
        y="Fraction",
        type="scatter",
        peak=6,
        shade=sns.color_palette("deep")[int(cluster_label.split()[-1])]
    )
    g.fig.suptitle(cluster_label, fontsize=14)
    g.set_axis_labels("Hour of Day", "Fraction of Day by day Consumption (largest meal)", fontsize=12)
    g.fig.tight_layout()
    g.fig.subplots_adjust(prime=0.95)  # regulate title spacing
    plt.present()

To know how people have been distributed throughout clusters, I visualized the variety of folks assigned to every cluster. The bar plot beneath exhibits the frequency of people grouped by their temporal dietary sample. This helps assess whether or not sure consuming behaviors — comparable to skipping meals, late-night consuming, or frequent snacking — are extra prevalent within the inhabitants.

Based mostly on the joint distribution plots, distinct temporal dietary behaviors emerge throughout clusters:

Cluster 0 (Versatile or Irregular Eater) reveals a broad dispersion of the biggest consuming events throughout each the 24-hour day and the fraction of each day caloric consumption.

Cluster 1 (Frequent Gentle Eaters) shows a extra evenly distributed consuming sample, the place no single consuming event exceeds 30% of the entire each day consumption, reflecting frequent however smaller meals all through the day. That is the cluster that almost certainly represents “regular eaters” — those that eat three comparatively balanced meals unfold all through the day. That’s due to low variance in timing and fraction per consuming occasion.

Cluster 2 (Early Heavy Eaters) is outlined by a really distinct and constant sample: people on this group eat virtually their complete each day caloric consumption (near 100%) in a single meal, predominantly through the early hours of the day (midnight to midday).

Cluster 3 (Late Night time Heavy Eaters) is characterised by people who eat almost all of their each day energy in a single meal through the late night or evening hours (between 6 PM and midnight). Like Cluster 2, this group displays a unimodal consuming sample with a very excessive fractional consumption (~1.0), indicating that the majority members eat as soon as per day, however in contrast to Cluster 2, their consuming window is considerably delayed.

CONCLUSION

On this undertaking, I explored how Modified Dynamic Time Warping (MDTW) will help uncover temporal dietary patterns — focusing not simply on what we eat, however when and how a lot. Utilizing artificial information to simulate lifelike consuming behaviors, I demonstrated how MDTW can cluster people into distinct profiles like irregular or versatile eaters, frequent mild eaters, early heavy eaters and later evening eaters based mostly on the timing and magnitude of their meals.

Whereas the outcomes present that MDTW mixed with Ok-Medoids can reveal significant patterns in consuming behaviors, this strategy isn’t with out its challenges. Because the dataset was synthetically generated and clustering was based mostly on a single initialization, there are a number of caveats value noting:

• The clusters seem messy, probably as a result of the artificial information lacks sturdy, naturally separable patterns — particularly if meal instances and calorie distributions are too uniform.
• Some clusters overlap considerably, notably Cluster 0 and Cluster 1, making it tougher to differentiate between actually totally different behaviors.
• With out labeled information or anticipated floor reality, evaluating cluster high quality is tough. A possible enchancment could be to inject identified patterns into the dataset to check whether or not the clustering algorithm can reliably get well them.

Regardless of these limitations, this work exhibits how a nuanced distance metric — designed for irregular, real-life patterns — can floor insights conventional instruments might overlook. The methodology will be prolonged to personalised well being monitoring, or any area the place when issues occur issues simply as a lot as what occurs.

I’d love to listen to your ideas on this undertaking — whether or not it’s suggestions, questions, or concepts for the place MDTW might be utilized subsequent. That is very a lot a piece in progress, and I’m all the time excited to be taught from others.

For those who discovered this convenient, have concepts for enhancements, or need to collaborate, be happy to open a difficulty or ship a Pull Request on GitHub. Contributions are greater than welcome!

Thanks a lot for studying all the best way to the top — it actually means rather a lot.

Code on GitHub : https://github.com/YagmurGULEC/mdtw-time-series-clustering

REFERENCES

[1] Khanna, Nitin, et al. “Modified dynamic time warping (MDTW) for estimating temporal dietary patterns.” 2017 IEEE World Convention on Sign and Data Processing (GlobalSIP). IEEE, 2017.