FEATURE ENGINEERING for Machine Learning | by Yasin Sutoglu | May, 2025

A) ENCODING

“Altering the best way variables are represented”

1. Binning

This primarily means dividing steady or different numerical options into distinct teams. By making use of area data, you might be able to engineer classes and options that higher emphasize vital tendencies in your knowledge.

Now, Let’s clarify this technique utilizing an instance of digital voting dataset.

I’ve chosen 2 numerical variables to work with:

1. age: a registered voter’s age on the finish of the election 12 months
2. birth_year: the 12 months a registered voter was born

Utilizing np.the place() to Point out Thresholds

We will create an indicator variable for this threshold utilizing np.the place() which takes 3 arguments:

1. a situation
2. what to return if the situation is met
3. what to return if the situation is just not met

The next code creates a brand new function, first_pres_elec, based mostly on a person’s age:

df['first_pres_elec'] = np.the place(df['age']<22, 1, 0)

Defining Bins with pd.reduce()

We will create the era bins utilizing pd.reduce() . We’ll must outline the suitable labels for every group, in addition to the bin edges (reduce off beginning years).

# EXAMPLE-1
## Bin registered voters into era teams utilizing pd.reduce
# Outline group labels
cut_labels = ['Greatest-Silent', 'Boomer', 'GenX', 'Millennial', 'GenZ']
# Outline bin edges
cut_bins = [0, 1945, 1964, 1980, 1996, 2100]
# Create a brand new column grouping birth_year into generations
df['cut_generation'] = pd.reduce(df['birth_year'], bins=cut_bins, labels=cut_labels)

# EXAMPLE-2
# Outline group labels
cut_labels = ['Teens', "20's", "30's", "40's", "50's", "60's", "70's", "80's", "90's", "100's"]
# Outline bin edges
cut_bins = np.arange(10, 111, 10)
# Create a brand new column grouping birth_year into generations
df['cut_age'] = pd.reduce(df['age'], bins=cut_bins, labels=cut_labels)

2. Label/Binary Encoding

The courses of a categorical variable are known as “labels”. Label encoding might be completed on ordinal (ordered) categorical variables.

3. One-hot Encoding

It will be dangerous to label encode the nominal categorical variable beneath. The transformation to be made for that is one-hot encoding.

Right here, to keep away from the dummy (multicollinearity) variable entice, the primary class (GS) is deleted with drop_first=True. If there are n categorical variables, we will categorical n-1 as a brand new numerical variable. As a result of there’s a thought that if it isn’t one among n-1, it’s the the rest.

dummy variable entice: Since they seem as variable traps that may be created on one another(overlapping), they trigger incorrect correlation within the evaluation.

4. Uncommon Encoding

If there are too many courses to be included in one-hot encoding, we will use Uncommon Encoding right here. This will increase the effectivity of the hyperparameter optimization course of.

Earlier than passing the explicit variables right here by one-hot encoding, we keep in mind those with low statement numbers within the mannequin and use this technique to improve the encode high quality. We don’t need to create too many pointless variables as a result of it impacts processes equivalent to iteration processes. It’ll critically have an effect on the division and branching processes in tree strategies. So, we will work on lowering the variety of observations that result in overfitting, and merge the classes with low frequency.

B) FEATURE TRANSFORMATION & SCALING

1. FEATURE TRANSFORMATION

As we all know, our real-life knowledge is commonly very unorganized and messy and with out knowledge preprocessing, there isn’t a that means in making a machine studying mannequin. Some Machine Studying fashions, like Linear and Logistic regression, assume that the variables observe a regular distribution. Extra probably, variables in actual datasets will observe a skewed distribution as acknowledged in first sentence. By making use of some transformations to those skewed variables conserving the essence of the info, we will map this skewed distribution to a regular distribution so, this will improve the efficiency of our fashions.

Function Transformation is a method we must always at all times use whatever the mannequin we’re utilizing, whether or not it’s a classification job or regression job, or be it an unsupervised studying mannequin.

Function transformation is a mathematical transformation wherein we apply a mathematical formulation to a specific column(function) and remodel the values that are helpful for our additional evaluation. By this technique, creating new options(extra explanatory energy in a unique house relatively than within the authentic house) from present options that will assist in bettering the mannequin efficiency.

Function transformation can be used for Function Discount. It may be completed in some ways, by linear mixtures of authentic options or through the use of non-linear capabilities.

Because the outcomes of those phrases, Function transformation helps machine studying algorithms to converge quicker and may enhance our mannequin efficiency.

There are 3 forms of Function transformation methods:

1. Operate Transformers
2. Energy Transformers
3. Quantile Transformers

— Operate Transformers —

Operate transformers are the kind of function transformation method that makes use of a specific perform to rework the info to the traditional distribution.

There’s no rule of thumb for the number of perform transformers, the perform might be designed by anybody good at area data of the info, however largely there are 5 forms of perform transformers which are used and which additionally remedy the problem of regular distribution nearly each time.

• Log Transformer: This is without doubt one of the easiest transformations on the info wherein the log is utilized to each single distribution of the info and the consequence from the log is taken into account the ultimate day to feed the machine studying algorithms. This performs so nicely on the right-skewed knowledge. It transforms the right-skewed knowledge into usually distributed knowledge so nicely.(By experiments). This transformation is not utilized to these options which have destructive values. It converts knowledge from additive Scale to multiplicative scale i,e, linearly distributed knowledge.

Extra, the log operation had a twin position:

1- Decreasing the influence of too-low values

2- Decreasing the influence of too-high values.

from sklearn.preprocessing import FunctionTransformer
remodel = FunctionTransformer(func=np.log1p)
transformed_data = remodel.fit_transform(knowledge)

• Sq. Transformer: In this transformer, the info is utilized with the sq. perform, the place the sq. of each single statement shall be thought of as the ultimate remodeled knowledge. If there’s a non-linear relationship between a function and the goal variable, making use of the sq. remodel can assist seize this relationship. It may possibly allow a linear mannequin to raised match the info, as it will possibly mannequin curved or quadratic patterns

import numpy as np
tranformed_data = np.sq.(knowledge)

• Sq. Root Transformer: On this remodel, the sq. root of the info is calculated. This remodel performs so nicely on the left-skewed knowledge and effectively remodeled the left-skewed knowledge into usually distributed knowledge. This transformation is outlined just for optimistic numbers.

import numpy as np 
tranformed_data = np.sqrt(knowledge)

• Reciprocal Transformer: On this transformation, the reciprocal of each statement (1/x) is taken into account. This remodel is beneficial in a number of the datasets because the reciprocal of the observations(the connection between the function and the goal variable could also be inversely proportional) works nicely to attain regular distributions. It’s a highly effective transformation with a radical impact. This transformation is just not outlined for zero. The reciprocal remodel can assist stabilize the variance of a function, significantly if the variance will increase because the function values improve. This may be useful in fashions that assume fixed variance, equivalent to linear regression.

import numpy as np
tranformed_data = np.reciprocal(knowledge)

• Customized Transformer: In each dataset, the log and sq. root transforms can’t be used, as each knowledge can have completely different patterns and complexity. Primarily based on the area data of the info, customized transformations might be utilized to rework the info into a standard distribution. Suppose you could have your personal Python perform to rework the info. Sklearn additionally supplies the power to use this remodel to our dataset utilizing what is named a Operate Transformer. The customized transformers right here might be any perform or parameter like sin, cos, tan, dice, and so on.

from sklearn.preprocessing import FunctionTransformer
transformer = FunctionTransformer(np.log2, validate = True)
df_scaled[col_names] = transformer.remodel(options.values)

— Energy Transformers —

Like another scalers we studied above, the Energy Transformer additionally adjustments the distribution of the variable, as in, it makes it extra Gaussian(regular).

We’re acquainted with comparable energy transforms equivalent to sq. root, and dice root transforms, and log transforms.

Nevertheless, to make use of them, we have to first research the unique distribution, after which make a selection. The Energy Transformer really automates this choice making by introducing a parameter known as lambda(λ).

It decides on a generalized energy remodel by discovering the very best worth of lambda utilizing both the:

• Field-Cox Transformer: There are primarily two circumstances related to the facility on this remodel, which is lambda equals zero and never equal to zero.

Right here the lambda is the facility utilized to each knowledge statement. Primarily based upon the iteration method each single worth of the lambda is examined and the very best match worth of the lambda is then utilized to the info to rework it.

• λ=0: The pure logarithm transformation (ln⁡(y)).
• λ=1: No transformation utilized (y).
• λ=−1: The reciprocal transformation (1/y).
• λ=0.5: The sq. root transformation (sqrt{y}​).

Right here the remodeled worth of each knowledge statement will lie between 5 to -5. One main drawback related to this transformation method is that this system can solely be utilized to optimistic observations. it isn’t relevant for destructive and 0 values of the info observations.

from sklearn.preprocessing import PowerTransformer
boxcox = PowerTransformer(technique='box-cox')
data_transformed = boxcox.fit_transform(knowledge)

• Yeo-Johnson Transformer: That is a sophisticated type of a field cox transformations method the place it may be utilized to even zero and destructive values of information observations additionally.

On this transformation method, y represents the suitable worth of Xi. In scikit study the default parameter is ready to Yeo Johnson within the Energy Transformer class.

from sklearn.preprocessing import PowerTransformer
boxcox = PowerTransformer()
data_transformed = boxcox.fit_transform(knowledge)

It’s useful to know that Field-Cox works with solely optimistic values, whereas Yeo-Johnson works with each optimistic and destructive values.

— Quantile Transformers —

Quantile transformation method is the kind of function transformation method that may be utilized to NY numerical knowledge observations.

On this transformation method, the enter knowledge might be fed to this transformer the place this transformer makes the distribution of the output knowledge regular to fed to the additional machine studying algorithm.

Right here there’s a parameter known as output_distribution, which worth might be set to uniform or regular.

from sklearn.preprocessing import QuantileTransformer
quantile_trans = QuantileTransformer(output_distribution='regular')
data_transformed = quantile.fit_transform(knowledge)

2. FEATURE SCALING (Normalization-Standardization)

Normalization and Standardization are two of the most typical methods utilized in knowledge transformation which goals to scale and remodel the info such that the options have comparable scales, which makes it straightforward for the machine studying algorithm to study and converge.

Our Objectives

• To get rid of the measurement variations between variables. In different phrases, our purpose is to judge all variables below equal circumstances.
• To forestall inflation in clustering operations equivalent to KNN. (In distance-based strategies, variables with massive values ​​​​present dominance. Particularly when some distance-based or similarity-dissimilarity-based strategies equivalent to KNN, Ok-means and PCA are used, the truth that the scales listed below are completely different from one another causes bias within the distance-closeness, similarity-dissimilarity calculations.)
• To shorten the coaching length of algorithms utilizing Gradient Descent.

a. Normalization (Min-Max Scaler)

The primary goal of normalization is to rescale the options to a regular vary of values which is often [0,1] or [-1,1]. Normalization is often used when completely different options have completely different vary of values and a few function would possibly contribute extra to the mannequin studying course of, normalization helps in equalizing the vary of the options and makes positive that the options contribute equally to the educational algorithm.

import pandas as pd
from sklearn.preprocessing import MinMaxScaler
# Instance DataFrame with an 'age' column
knowledge = {
'age': [21, 30, 25, 35, 40]
}
df = pd.DataFrame(knowledge)
# Initialize MinMaxScaler
scaler = MinMaxScaler()
# Match and remodel the 'age' column
df['scaled_age'] = scaler.fit_transform(df[['age']])
# Print the unique and scaled DataFrame
print("Authentic DataFrame:")
print(df[['age']])
print("nDataFrame with scaled age:")
print(df[['scaled_age']])

b. Standardization (z-score scaler / Variance Scaling / z-score normalization)

Primarily, this technique converts the imply of a variable to 0 and its commonplace deviation to 1. In different phrases, the target of standardization is to rework the function such that the worth of imply turns into 0 and the worth of normal deviation turns into 1.

Standardization is often helpful when options have completely different scales however observe regular distribution, it helps machine studying algorithms which depends on gradient based mostly optimization to converge at a quicker price.

#Lets do an instance
import numpy as np
# Assuming X is your function matrix
X = np.array([[1, 2, 3],
[4, 5, 6],
[100, 500, 950]])
# Create a StandardScaler occasion
scaler = StandardScaler()
# Match the scaler on the info and remodel it
X_standardized = scaler.fit_transform(X)
print("Authentic Knowledge:n", X)
print("nStandardized Knowledge:n", X_standardized)

c. MaxAbsScaler

The MaxAbs scaler takes absolutely the most worth of every column and divides every worth within the column by the utmost worth.

Thus, it first takes absolutely the worth of every worth within the column after which takes the utmost worth out of these. This operation scales the info between the vary [-1, 1].

from sklearn.preprocessing import MaxAbsScaler
scaler = MaxAbsScaler()
df_scaled[col_names] = scaler.fit_transform(options.values)

d. RobustScaler

In case you have observed within the scalers we used up to now, every of them was utilizing values just like the imply, most and minimal values of the columns. All these values are delicate to outliers. If there are too many outliers within the knowledge, they’ll affect the imply and the max worth or the min worth. Thus, even when we scale this knowledge utilizing the above strategies, we can not assure a balanced knowledge with a standard distribution.

The Strong Scaler, because the title suggests is just not delicate to outliers. This scaler;

• Removes the median from the info
• Scales the info by the InterQuartile Vary(IQR = Q3 - Q1)

x_scaled = (x — Q1)/(Q3 — Q1)

from sklearn.preprocessing import RobustScaler
scaler = RobustScaler()
df_scaled[col_names] = scaler.fit_transform(options.values)
print(df_scaled)

e. Unit Vector Scaler/Normalizer

Normalization is the method of scaling particular person samples to have unit norm. Essentially the most fascinating half is that in contrast to the opposite scalers which work on the person column values, the Normalizer works on the rows! Every row of the dataframe with at the very least one non-zero part is rescaled independently of different samples in order that its norm (L1, L2, or inf) equals one.

Identical to MinMax Scaler, the Normalizer additionally converts the values between 0 and 1, and between -1 to 1 when there are destructive values in our knowledge.

Nevertheless, there’s a distinction in the best way it does so.

• If we’re utilizing L1 norm, the values in every column are transformed in order that the sum of their absolute values alongside the row = 1
• If we’re utilizing L2 norm, the values in every column are first squared and added in order that the sum of their absolute values alongside the row = 1

from sklearn.preprocessing import Normalizer
scaler = Normalizer(norm = 'l2')
# norm = 'l2' is default
df_scaled[col_names] = scaler.fit_transform(options.values)
print(df_scaled)

In abstract, standardization processes needs to be carried out to forestall knowledge from crushing one another, to extend the effectivity of the optimization technique, and to forestall swelling in clustering by way of distance-based strategies (KNN and so on.)

Whereas StandartScaler tries to offer a standard distribution to the info, MinMaxScaler tries to suit the values ​​right into a sure vary.

Tree strategies are usually not affected by lacking values, outliers, and standardization.

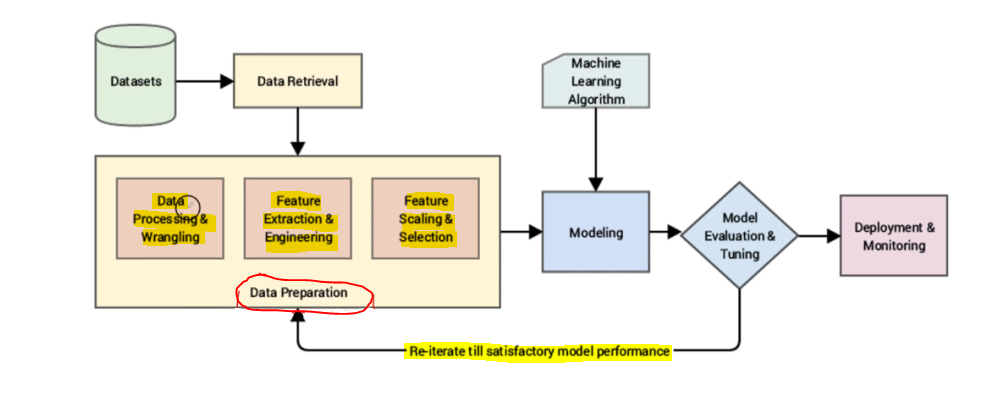
C) FEATURE EXTRACTION & SELECTION

1. FEATURE EXTRACTION

The method of making new options or modifying the prevailing function to enhance the efficiency of machine studying mannequin is named Function Extraction. It helps in creating extra informative and efficient illustration of patterns current in knowledge by combining and remodeling the given options. By function extraction we will improve our mannequin efficiency and generalization means. Some commonest strategies:

• Polynomial Options
  Creating new options by taking polynomial options into consideration, by elevating present options to an influence or by multiplying them collectively. Polynomial options are utilized in numerous situations the place the connection between the dependent and impartial variables is non-linear. This method can add flexibility to principally the linear fashions which are well-known like linear regression, logistic regression and so on. Furthermore, Some machine studying algorithms, like polynomial regression or sure forms of help vector machines (SVMs), could require or profit from polynomial options to carry out higher. We will apply regularization with polynomial options to cut back the danger of overfitting.

import pandas as pd
from sklearn.preprocessing import PolynomialFeatures
# Pattern knowledge
knowledge = {
'feature1': [1, 2],
'feature2': [4, 5]
}
df = pd.DataFrame(knowledge)
# Initialize the PolynomialFeatures with the specified diploma
poly = PolynomialFeatures(diploma=3, include_bias=False)
# Match and remodel the info
poly_features = poly.fit_transform(df)
# Present the polynomial options
print(poly_features)
#Output:
[[  1.   4.   1.   4.  16.   1.   4.  16.  64.]
[  2.   5.   4.  10.  25.   8.  20.  50. 125.]]
# Here is the detailed breakdown of the columns within the output:
# feature1
# feature2
# feature1^2
# feature1 * feature2
# feature2^2
# feature1^3
# feature1^2 * feature2
# feature1 * feature2^2
# feature2^3

• Interplay Phrases
  We will mix two or extra options collectively to provide a brand new function, this helps machine studying algorithms specifically linear fashions to establish and leverage the mixed impact of various options on the end result. The interplay phrases uncovers the patterns that aren’t targeted if particular person options are thought of, these phrases helps in understanding the connection between completely different variables and the impact of change in a single function on the behaviour of one other. For instance suppose we’re modelling a easy regression drawback of home worth prediction, there are completely different home whose size and width of span is given allow them to be ‘l’, ‘b’ respectively. It’s higher to introduce a brand new function space which is the multiplication on size and width, or ‘l.b’, which is a greater indication of home worth.

from sklearn.preprocessing import PolynomialFeatures
# Pattern knowledge
knowledge = {
'feature1': [1, 2, 3, 4, 5],
'feature2': [2, 3, 4, 5, 6]
}
df = pd.DataFrame(knowledge)
# Initialize PolynomialFeatures to seize interplay phrases
interplay = PolynomialFeatures(diploma=2, interaction_only=True, include_bias=False)
# Match and remodel the info to create interplay options
interaction_features = interplay.fit_transform(df)
# Convert the consequence to a DataFrame for higher readability
interaction_df = pd.DataFrame(interaction_features, columns=interplay.get_feature_names_out(df.columns))
# Present the unique and interplay options
print(interaction_df)

The distinction between Polynomial options and interplay options is that in contrast to polynomial options, interplay options don’t embrace the person options raised to powers, they solely embrace the interplay phrases.

• Area-Particular Function
  We should take into account creating options which are extremely related and informative about the issue in hand. This course of includes deep understanding of the area on work we’re in, in addition to the data of the info introduced to us. This helps us create new options that may not be that a lot of use instantly however is important for area we’re at present performing evaluation in

Primarily, It means deriving a variable/function from uncooked knowledge.

It may be evaluated in two scopes:
1. From Structural Variables

2. From Non-Structural Variables

Additionally, For Picture Processing, I’ve to do one thing (Convolution + Pooling) in order that our picture knowledge might be expressed with linear algebra; Particularly, It must be transformed to pixel-based mathematical expressions, density variations in sure locations, colour distributions, and so on. can be utilized.

2. FEATURE SELECTION

There are three typese of function choice methods:

• Filter Strategies: Filter strategies choose up the intrinsic properties of the options measured by way of univariate statistics as a substitute of cross-validation efficiency. These strategies are quicker and fewer computationally costly than wrapper strategies. When coping with high-dimensional knowledge, it’s computationally cheaper to make use of filter strategies (Data Acquire, Chi-square Check(Choose Ok-Finest), Fisher’s Rating, Correlation Coefficient, Variance Threshold, Imply Absolute Distinction (MAD))

• Wrapper Strategies: Wrappers require some technique to look the house of all doable subsets of options, assessing their high quality by studying and evaluating a classifier with that function subset. The function choice course of is predicated on a particular machine studying algorithm we try to suit on a given dataset. It follows a grasping search strategy by evaluating all of the doable mixtures of options towards the analysis criterion. The wrapper strategies often lead to higher predictive accuracy than filter strategies.(Ahead Function Choice, Backward Function Elimination, Exhaustive Function Choice, Recursive Function Elimination)

• Embedded Strategies(SelectFromModel): These strategies embody the advantages of each the wrapper and filter strategies by together with interactions of options but additionally sustaining cheap computational prices. Embedded strategies are iterative within the sense that takes care of every iteration of the mannequin coaching course of and punctiliously extract these options which contribute essentially the most to the coaching for a specific iteration. (LASSO Regularization (L1), Random Forest Significance, Gradient Boosting)

a. FILTER METHODs

1. Data Acquire

Data achieve calculates the discount in entropy from the transformation of a dataset. It may be used for function choice by evaluating the Data achieve of every variable within the context of the goal variable.

from sklearn.feature_selection import mutual_info_classif
import matplotlib.pyplot as plt
%matplotlib inline
importances = mutual_info_classif(X, Y)
feat_importances = pd.Collection(importances, dataframe.columns[0:len(dataframe.columns)-1])
feat_importances.plot(type='barh', colour = 'teal')
plt.present()

2. Chi-square Check (Choose Ok-Finest)

The Chi-square check is used for categorical options in a dataset. We calculate Chi-square between every function and the goal and choose the specified variety of options with the very best Chi-square scores. With a purpose to appropriately apply the chi-squared to check the relation between numerous options within the dataset and the goal variable, the next circumstances need to be met: the variables need to be categorical, sampled independently, and values ought to have an anticipated frequency larger than 5.

from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2
# Convert to categorical knowledge by changing knowledge to integers
X_cat = X.astype(int)
# Three options with highest chi-squared statistics are chosen
chi2_features = SelectKBest(chi2, ok=3)
X_kbest_features = chi2_features.fit_transform(X_cat, Y)
# Decreased options
print('Authentic function quantity:', X_cat.form[1])
print('Decreased function quantity:', X_kbest_features.form[1])

3. Fisher’s Rating

Fisher rating is without doubt one of the most generally used supervised function choice strategies. The algorithm we’ll use returns the ranks of the variables based mostly on the fisher’s rating in descending order. We will then choose the variables as per the case.

from skfeature.perform.similarity_based import fisher_score
import matplotlib.pyplot as plt
%matplotlib inline
# Calculating scores
ranks = fisher_score.fisher_score(X, Y)
# Plotting the ranks
feat_importances = pd.Collection(ranks, dataframe.columns[0:len(dataframe.columns)-1])
feat_importances.plot(type='barh', colour='teal')
plt.present()

4. Correlation Coefficient

Correlation is a measure of the linear relationship between 2 or extra variables. By correlation, we will predict one variable from the opposite. The logic behind utilizing correlation for function choice is that good variables correlate extremely with the goal. Moreover, variables needs to be correlated with the goal however uncorrelated amongst themselves.

If two variables are correlated, we will predict one from the opposite. Due to this fact, if two options are correlated, the mannequin solely wants one, because the second doesn’t add further info. We’ll contact the Pearson Correlation.

We have to set an absolute worth, say 0.5, as the brink for choosing the variables. If we discover that the predictor variables are correlated, we will drop the variable with a decrease correlation coefficient worth than the goal variable. We will additionally compute a number of correlation coefficients to verify whether or not greater than two variables correlate. This phenomenon is named multicollinearity.

import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
# Correlation matrix
cor = dataframe.corr()
# Plotting Heatmap
plt.determine(figsize=(10,6))
sns.heatmap(cor, annot=True)
plt.present()

5. Variance Threshold

The variance threshold is an easy baseline strategy to function choice. It removes all options whose variance doesn’t meet some threshold. By default, it removes all zero-variance options, i.e., options with the identical worth in all samples. We assume that options with the next variance could include extra helpful info, however observe that we aren’t taking the connection between function variables or function and goal variables into consideration, which is without doubt one of the drawbacks of filter strategies.

from sklearn.feature_selection import VarianceThreshold
# Resetting the worth of X to make it non-categorical
X = array[:, 0:8]
v_threshold = VarianceThreshold(threshold=0)
v_threshold.match(X)  # match finds the options with zero variance
v_threshold.get_support()

The get_support returns a Boolean vector the place True means the variable doesn’t have zero variance.

b. WRAPPER METHODs

1. Ahead Function Choice

That is an iterative technique whereby we begin with the performing options towards the goal options. Subsequent, we choose one other variable that offers the very best efficiency together with the primary chosen variable. This course of continues till the preset criterion is achieved.

# Import needed libraries
from mlxtend.feature_selection import SequentialFeatureSelector
# Create a Sequential Function Selector object utilizing a logistic regression mannequin
# k_features='finest' selects the optimum variety of options
# ahead=True signifies ahead function choice
# n_jobs=-1 makes use of all out there cores for parallel processing
ffs = SequentialFeatureSelector(lr, k_features='finest', ahead=True, n_jobs=-1)
# Match the Sequential Function Selector to the info
ffs.match(X, y)
# Get the chosen options
options = listing(ffs.k_feature_names_)
# Convert function names to integers (if needed)
options = listing(map(int, options))
# Match the logistic regression mannequin utilizing solely the chosen options
lr.match(X_train[:, features], y_train)
# Make predictions on the coaching knowledge utilizing the chosen options
y_pred = lr.predict(X_train[:, features])

2. Backward Function Elimination

This technique works precisely reverse to the Ahead Function Choice technique. Right here, we begin with all of the options out there and construct a mannequin. Subsequent, we choose the variable from the mannequin, which provides the finest analysis measure worth. This course of is sustained till the preset criterion is achieved.

# Import needed libraries
from sklearn.linear_model import LogisticRegression
from mlxtend.feature_selection import SequentialFeatureSelector
# Create a logistic regression mannequin with class weight balancing
lr = LogisticRegression(class_weight='balanced', solver='lbfgs', random_state=42, n_jobs=-1, max_iter=500)
# Match the logistic regression mannequin to the info
lr.match(X, y)
# Create a Sequential Function Selector object utilizing the logistic regression mannequin
# k_features='finest' selects the optimum variety of options
# ahead=False signifies backward function choice
# n_jobs=-1 makes use of all out there cores for parallel processing
bfs = SequentialFeatureSelector(lr, k_features='finest', ahead=False, n_jobs=-1)
# Match the Sequential Function Selector to the info
bfs.match(X, y)
# Get the chosen options
options = listing(bfs.k_feature_names_)
# Convert function names to integers (if needed)
options = listing(map(int, options))
# Match the logistic regression mannequin utilizing solely the chosen options
lr.match(X_train[:, features], y_train)
# Make predictions on the coaching knowledge utilizing the chosen options
y_pred = lr.predict(X_train[:, features])

3. Exhaustive Function Choice

That is essentially the most sturdy function choice technique coated up to now. It is a brute-force analysis of every function subset. This implies it tries each doable mixture of the variables and returns the best-performing subset.

# Import needed libraries
from mlxtend.feature_selection import ExhaustiveFeatureSelector
from sklearn.ensemble import RandomForestClassifier
# Create an Exhaustive Function Selector object utilizing a Random Forest classifier
# min_features=4 units the minimal variety of options to contemplate
# max_features=8 units the utmost variety of options to contemplate
# scoring='roc_auc' specifies the scoring metric
# cv=2 specifies the variety of cross-validation folds
efs = ExhaustiveFeatureSelector(RandomForestClassifier(), min_features=4, max_features=8, scoring='roc_auc', cv=2)
# Match the Exhaustive Function Selector to the info
efs.match(X, y)
# Print the chosen options
selected_features = X_train.columns[list(efs.best_idx_)]
print(selected_features)
# Print the ultimate prediction rating
print(efs.best_score_)

4. Recursive Function Elimination

Given an exterior estimator that assigns weights to options (e.g., the coefficients of a linear mannequin), the aim of recursive function elimination (RFE) is to pick out options by recursively contemplating smaller and smaller units of options. First, the estimator is educated on the preliminary set of options, and every function’s significance is obtained both by a coef_ attribute or a feature_importances_ attribute.
Then, the least vital options are pruned from the present set of options. That process is recursively repeated on the pruned set till the specified variety of options to pick out is finally reached.

# Import needed libraries
from sklearn.feature_selection import RFE
# Create a Recursive Function Elimination object utilizing a logistic regression mannequin
# n_features_to_select=7 specifies the variety of options to pick out
rfe = RFE(lr, n_features_to_select=7)
# Match the Recursive Function Elimination object to the info
rfe.match(X_train, y_train)
# Make predictions on the coaching knowledge utilizing the chosen options
y_pred = rfe.predict(X_train)

c. EMBEDDED METHODs

1. LASSO Regularization (L1)

Regularization consists of including a penalty to the completely different parameters of the machine studying mannequin to cut back the liberty of the mannequin, i.e., to keep away from over-fitting. In linear mannequin regularization, the penalty is utilized over the coefficients that multiply every predictor. From the several types of regularization, Lasso or L1 has the property that may shrink a number of the coefficients to zero. Due to this fact, that function might be faraway from the mannequin.

# Import needed libraries
from sklearn.linear_model import LogisticRegression
from sklearn.feature_selection import SelectFromModel
# Create a logistic regression mannequin with L1 regularization
logistic = LogisticRegression(C=1, penalty='l1', solver='liblinear', random_state=7).match(X, y)
# Create a SelectFromModel object utilizing the logistic regression mannequin
mannequin = SelectFromModel(logistic, prefit=True)
# Rework the function matrix utilizing the SelectFromModel object
X_new = mannequin.remodel(X)
# Get the indices of the chosen options
selected_columns = selected_features.columns[selected_features.var() != 0]
# Print the chosen options
print(selected_columns)

2. Random Forest Significance

Random Forests is a sort of Bagging Algorithm that aggregates a specified variety of choice timber. The tree-based methods utilized by random forests naturally rank by how nicely they enhance the purity of the node, or in different phrases, a lower within the impurity (Gini impurity) over all timber. Nodes with the best lower in impurity occur in the beginning of the timber, whereas notes with the least lower in impurity happen on the finish of the timber. Thus, by pruning timber beneath a specific node, we will create a subset of crucial options.

# Import needed libraries
from sklearn.ensemble import RandomForestClassifier
# Create a Random Forest classifier together with your hyperparameters
mannequin = RandomForestClassifier(n_estimators=340)
# Match the mannequin to the info
mannequin.match(X, y)
# Get the significance of the ensuing options
importances = mannequin.feature_importances_
# Create a knowledge body for visualization
final_df = pd.DataFrame({'Options': pd.DataFrame(X).columns, 'Importances': importances})
final_df.set_index('Importances')
# Kind in ascending order for higher visualization
final_df = final_df.sort_values('Importances')
# Plot the function importances in bars
final_df.plot.bar(colour='teal')

3. DIMENSIONALTY REDUCTION

Dimentionality discount is the method of lowering the variety of options within the dataset whereas preserving the knowledge that the unique dataset conveys. It’s typically thought of good to cut back the size of extremely dimensional dataset to cut back the computational complexity and cut back the probabilities of overfitting. There are commont three sorts:

a. Principal Part Evaluation(PCA)
PCA is the most typical dimensionality discount method utilized in machine studying which transforms increased dimension knowledge into decrease dimension knowledge retaining the knowledge of the unique dataset. PCA offers with the era of principal parts by standardization of information, discovering covariance matrix of the info after which arranging the eigenvector obtained from the covariance ( variance means info selection ) matrix based on eigen values in descending order. In PCA the unique knowledge is projected onto the principal parts to acquire decrease dimensional knowledge.

• The coordinate system is modified and correlation is eradicated.

from sklearn.decomposition import PCA
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
home = pd.read_csv('home.csv', index_col=0) 
print(home.form)
# (1460, 80)
X = df_drop_cols_dummy.drop("SalePrice", axis = 1)
y = df_drop_cols_dummy["SalePrice"]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
pca = PCA(n_components=154) #finest "n" might be discovered iterative computation 
pca.match(X_train)
X_new_train = pca.remodel(X_train)
X_new_test = pca.remodel(X_test)
print(X_new_train.form)

b. Linear Discriminant Evaluation

Linear Discriminant Evaluation (LDA) is a statistical method for categorizing knowledge into teams. It identifies patterns in options to differentiate between completely different courses. As an example, it could analyze traits like measurement and colour to categorise fruits as apples or oranges. LDA goals to discover a straight line or aircraft that finest separates these teams whereas minimizing overlap inside every class. By maximizing the separation between courses, it permits correct classification of latest knowledge factors. In easier phrases, LDA helps make sense of information by successfully discovering essentially the most environment friendly strategy to separate completely different classes. Consequently, this aids in duties like sample recognition and classification.

# Importing required libraries:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn.metrics import confusion_matrix
# Getting ready dataset:
from sklearn.datasets import load_wine
dt = load_wine()
X = dt.knowledge
y = dt.goal
lda = LinearDiscriminantAnalysis()
lda_t = lda.fit_transform(X,y)
plt.xlabel('LD1')
plt.ylabel('LD2')
plt.scatter(lda_t[:,0],lda_t[:,1],c=y,cmap='rainbow',edgecolors='r')
# classification half
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3)
lda.match(X_train,y_train)
y_pred = lda.predict(X_test)
print(accuracy_score(y_test,y_pred))
print(confusion_matrix(y_test,y_pred))

c. t-Distributed Stochastic Neighbor Embedding

t-SNE is a non-linear dimensionality discount method used for visualizing high-dimensional knowledge in a lower-dimensional house primarily in 2D or 3D. In contrast to linear strategies equivalent to Principal Part Evaluation (PCA), t-SNE give attention to preserving the native construction and sample of the info.
What t-SNE algorithm does is that it takes increased dimensional knowledge and finds out the similarities in between the info factors, such that if this knowledge level happens what’s the chance of the opposite knowledge level occurring, after which it does the identical with decrease dimensional knowledge and tries to cut back the divergence between the pairwise knowledge factors in excessive and low dimension house.

import numpy as np
import pandas as pd
import seaborn as sn
import matplotlib.pyplot as plt
from sklearn.manifold import TSNE
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import fetch_openml
mnist = fetch_openml('mnist_784', model=1)
d = mnist.knowledge  
l = mnist.goal  
df = pd.DataFrame(d)
df['label'] = l  
standardized_data = StandardScaler().fit_transform(df)
print(standardized_data.form) # (70000, 785)
data_1000 = standardized_data[0:1000, :]
labels_1000 = l[0:1000]
mannequin = TSNE(n_components = 2, random_state = 0)
tsne_data = mannequin.fit_transform(data_1000)
tsne_data = np.vstack((tsne_data.T, labels_1000)).T
tsne_df = pd.DataFrame(knowledge = tsne_data,
columns =("Dim_1", "Dim_2", "label"))
sn.scatterplot(knowledge=tsne_df, x='Dim_1', y='Dim_2',
hue='label', palette="vivid")
plt.present()

The scatter plot above exhibits how t-SNE has mapped the MNIST dataset right into a 2D house. The factors are grouped by digit and we will see that comparable digits (like 1s or 7s) are clustered collectively making it simpler to establish patterns and relationships within the knowledge.

Listed here are some helpful methods and ideas for function choice:

1. Perceive Your Knowledge: Earlier than choosing options, completely perceive your dataset. Know the area and the relationships between completely different options.
2. Filter Strategies: Use statistical measures like correlation, chi-square, or mutual info to rank options based mostly on their relevance to the goal variable.
3. Wrapper Strategies: Make use of algorithms like Recursive Function Elimination (RFE) or Ahead/Backward Choice, which choose subsets of options based mostly on the efficiency of a particular machine studying algorithm.
4. Embedded Strategies: Some machine studying algorithms inherently carry out function choice throughout coaching. Examples embrace LASSO (L1 regularization) and tree-based strategies like Random Forests.
5. Dimensionality Discount: Methods like Principal Part Evaluation (PCA) or t-distributed Stochastic Neighbor Embedding (t-SNE) can cut back the dimensionality of your knowledge whereas retaining many of the info.
6. Function Significance: For tree-based algorithms like Random Forest or Gradient Boosting Machines (GBM), you need to use the built-in function significance attribute to pick out crucial options.
7. Area Data: Leverage area experience to establish options which are prone to be vital. Generally, options that appear irrelevant on the floor could be essential when contemplating domain-specific insights.
8. Regularization: Regularization methods like LASSO (L1 regularization) penalize absolutely the measurement of the coefficients, successfully performing function choice by driving some coefficients to zero.
9. Cross-Validation: Carry out function choice inside every fold of cross-validation to make sure that your function choice course of is just not biased by the particular dataset splits.
10. Ensemble Strategies: Mix the outcomes of a number of function choice strategies to get a extra sturdy set of chosen options.

THANKS FOR YOUR READING EFFORT 🙂

REFERENCES:

1. James, G., Witten, D., Hastie, T., & Tibshirani, R. (2013). An introduction to statistical studying (1st ed.) [PDF]. Springer.
2. Nasima (2025, 07 Apr). Efficient Methods for Dealing with Lacking Values in Knowledge Evaluation. https://www.analyticsvidhya.com/blog/2021/10/handling-missing-value/
3. Jacob Murel Ph.D. What’s function engineering? https://www.ibm.com/think/topics/feature-engineering
4. W Brett Kennedy (Jan 7, 2025). An Overview of Function Choicehttps://medium.com/data-science/an-overview-of-feature-selection-1c50965551dd
5. T-distributed Stochastic Neighbor Embedding (t-SNE) Algorithm — ML.(19 Could, 2025).https://www.geeksforgeeks.org/ml-t-distributed-stochastic-neighbor-embedding-t-sne-algorithm/
6. Chirag Goyal (16 Oct, 2024). Function Transformations in Knowledge Science: A Detailed Walkthrough. https://www.analyticsvidhya.com/blog/2021/05/feature-transformations-in-data-science-a-detailed-walkthrough/
7. Prime Methods to Deal with Lacking Values Each Knowledge Scientist Ought to Know (Jan 31, 2023).https://www.datacamp.com/tutorial/techniques-to-handle-missing-data-values
8. Max Steele. (Apr 5, 2021). Function Engineering Examples: Binning Numerical Options. https://towardsdatascience.com/feature-engineering-examples-binning-numerical-features-7627149093d/
9. DataScienceSphere. (Jul 10, 2024). Function Transformation- A part of Function Engineering. https://medium.com/@datasciencejourney100_83560/feature-transformation-part-of-feature-engineering-dff2deaf59a2
10. Aman (01 Could, 2025). Function Choice in Machine Studying. https://www.analyticsvidhya.com/blog/2020/10/feature-selection-techniques-in-machine-learning/