Definition: SVM is a supervised machine studying algorithm used for Classification and Regression duties. It’s particularly highly effective in binary classification issues.
- Aim: Discover the greatest choice boundary (hyperplane) that separates lessons with most margin.
- In 2D: SVM finds a line that separates two lessons.
- In greater dimensions: It finds a hyperplane that separates the info.
SVM chooses the hyperplane that has the utmost distance (margin) from the closest information factors (help vectors).
Hyperplane
- A call boundary that separates completely different lessons.
- In 2D: line, 3D: aircraft, n-D: hyperplane
Margin
- The space between the hyperplane and the closest information level from both class.
- SVM maximizes this margin.
Assist Vectors
- Information factors closest to the hyperplane.
- These are essential in defining the hyperplane.
Most Margin Classifier
- The hyperplane with the utmost attainable margin is chosen.
- Choose Hyperplane
- Discover π+ (optimistic class) and π-(adverse class)
- Discover margin(d).
- Discover the worth of w and b (W.TX+b) such that the worth of d is most.
Worth of d : 2/||w||
Kernel Trick is a strong mathematical method that enables SVM to unravel non-linearly separable issues by implicity mapping information to a higher- dimensional area — with out really computing that rework.
It lets SVM discover a linear hyperplane in a non-linear downside by utilizing a particular perform known as a Kernel.
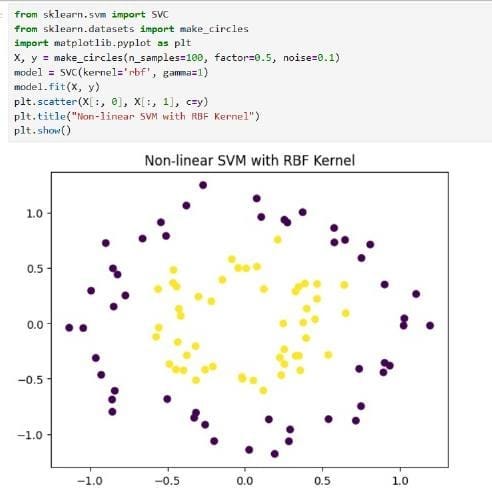
Suppose we’ve information which is formed like two concentric circles (internal = class 0, outer = class 1), no straight line can separate them in 2D.
However in greater dimensions, it could be attainable to separate them linearly. As a substitute of manually reworking your options, the kernel trick handles this neatly and effectively.
Let’s say we’ve a mapping perform:
¢(x) = R^n→ R^m
This maps enter options x from authentic area to a higer dimensional area. SVM makes use of the dot product ¢(xi).¢(xj) in that area. However computing ¢(x) explicitly might be very costly.
So as an alternative, we outline a kernel perform.
Ok(xi,xj) = ¢(xi).¢(xj)
This computes the dot product with out explicitly reworking the info and that is the kernel trick.
[kehne ka mtlb agr hmare data ko ek straight line se alg krna possible na ho toh kernel trick uss data ko ek higher-dimension space me le jata h — jaha pe SVM ek linear hyperplane ke through easily unko separate kr skta h. Aur achhi baat ye h ki SVM ko uss high dimensional transformation ko explicitly calculate krne ki zarurat nahi padti — bas ek kernel function use hota h jo ye kaam smartly background me kr deta h]
Think about In 2D our information seems to be like a circle inside one other circle. No line can cut up them. If we elevate the internal circle into 3D area utilizing a change like:
¢(x1,x2) = (x1²+x2²)
Now the internal circle turns into a degree above, and the outer circle stays beneath — now you’ll be able to separate them utilizing a flat aircraft.
That’s the magic of the kernel trick it lifts the info into an area the place linear separation is feasible.
- Can deal with advanced, non-linear choice boundaries
- No must manually rework options.
- Environment friendly: No must compute high-dimensional vectors.
- Works with many kinds of information (photographs, textual content, and so forth)
Actual life examples the place kernel trick is beneficial
- Handwriting Recognition (e.g., MNIST datasets)
- Picture Classification with advanced patterns.
- Bioinformatics (e.g., DNA Sequence classification)
- Spam filtering utilizing textual content options.
- C : Commerce off between margin width and classification error.
- kernel : Kind of kernel (‘linear’, ‘rbf’, ‘poly’)
- Gamma : Controls affect of a single coaching instance
- Diploma : Used with Polynomial kernel
- Efficient in high-dimensional areas
- Works effectively when no of options > no of samples
- Makes use of solely help vectors, so reminiscence environment friendly.
- Sturdy to overfitting in high- dimensional area (with correct C and kernel)
- Not appropriate giant datasets
- Poor efficiency when lessons overlap closely
- Requires cautious tuning of hyperparameters.
- Much less efficient with noisy information.