Understanding Matrices | Part 3: Matrix Transpose

the primary 2 tales of this collection [1], [2], we:

• Launched X-way interpretation of matrices
• Noticed bodily that means and particular circumstances of matrix-vector multiplication
• Seemed on the bodily that means of matrix-matrix multiplication
• Noticed its habits on a number of particular circumstances of matrices

On this story, I wish to share my ideas concerning the transpose of a matrix, denoted as A^T, the operation that simply flips the content material of the sq. desk round its diagonal.

In distinction to many different operations on matrices, it’s fairly straightforward to transpose a given matrix ‘A‘ on paper. Nevertheless, the bodily that means of that usually stays behind. Then again, it isn’t so clear why the next transpose-related formulation really work:

• (AB)^T = B^TA^T,
• (y, Ax) = (x, A^Ty),
• (A^TA)^T = A^TA.

On this story, I’m going to present my interpretation of the transpose operation, which, amongst others, will present why the talked about formulation are literally the way in which they’re. So let’s dive in!

However to start with, let me remind all of the definitions which are used all through the tales of this collection:

• Matrices are denoted with uppercase (like ‘A‘, ‘B‘), whereas vectors and scalars are denoted with lowercase (like ‘x‘, ‘y‘ or ‘m‘, ‘n‘).
• |x| – is the size of vector ‘x‘,
• rows(A) – variety of rows of matrix ‘A‘,
• columns(A) – variety of columns of matrix ‘A‘,
• A^T – the transpose of matrix ‘A‘,
• a^T_i,j – the worth on the i-th row and j-th column of the transposed matrix A^T,
• (x, y) – dot product of vectors ‘x‘ and ‘y‘ (i.e. “x₁y₁ + x₂y₂ + … + x_ny_n“).

Transpose vs. X-way interpretation

In part 1 of this collection – “matrix-vector multiplication” [1], I launched the X-way interpretation of matrices. Let’s recollect it with an instance:

From there, we additionally keep in mind that the left stack of the X-diagram of ‘A‘ may be related to rows of matrix ‘A‘, whereas its proper stack may be related to the columns.

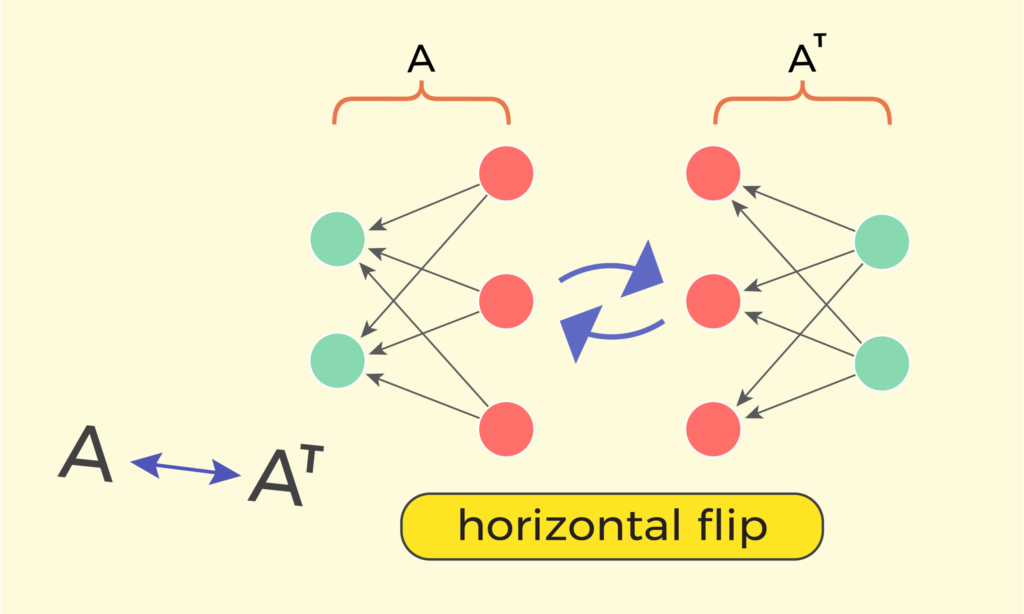
Now, if transposing a matrix is definitely flipping the desk round its important diagonal, it implies that all of the columns of ‘A‘ grow to be rows in ‘A^T‘, and vice versa.

And if transposing means altering the locations of rows and columns, then maybe we will do the identical on the X-diagram? Thus, to swap rows and columns of the X-diagram, we should always flip it horizontally:

Will the horizontally flipped X-diagram of ‘A‘ signify the X-diagram of ‘A^T‘? We all know that cell “a_i,j” is current within the X-diagram because the arrow ranging from the j‘th merchandise of the left stack, and directed in direction of the i‘th merchandise of the correct stack. After flipping horizontally, that very same arrow will begin now from the i‘th merchandise of the correct stack and might be directed to the j‘th merchandise of the left stack.

Which implies that the definition of transpose “a_i,j = a^T_j,i” does maintain.

Concluding this chapter, we now have seen that transposing matrix ‘A‘ is similar as horizontally flipping its X-diagram.

Transposing a series of matrices

Let’s see how decoding A^T as a horizontal flip of its X-diagram will assist us to uncover the bodily that means of some transpose-related formulation. Let’s begin with the next:

[begin{equation*}
(AB)^T = B^T A^T
end{equation*}]

which says that transposing the multiplication “A*B” is similar as multiplying transpositions A^T and B^T, however in reverse order. Now, why does the order really grow to be reversed?

From part 2 of this collection – “matrix-matrix multiplication” [2], we keep in mind that the matrix multiplication “A*B” may be interpreted as a concatenation of X-diagrams of ‘A‘ and ‘B‘. Thus, having:

y = (AB)x = A*(Bx)

will power the enter vector ‘x‘ to go at first by the transformation of matrix ‘B‘, after which the intermediate outcome will undergo the transformation of matrix ‘A‘, after which the output vector ‘y‘ might be obtained.

And now the bodily that means of the method “(AB)^T = B^TA^T” turns into clear: flipping horizontally the X-diagram of the product “A*B” will clearly flip the separate X-diagrams of ‘A‘ and the one among ‘B‘, however it additionally will reverse their order:

Within the earlier story [2], we now have additionally seen {that a} cell c_i,j of the product matrix ‘C=A*B‘ describes all of the attainable methods through which x_j of the enter vector ‘x‘ can have an effect on y_i of the output vector ‘y = (AB)x‘.

Now, when transposing the product “C=A*B“, thus calculating matrix C^T, we wish to have the mirroring impact – so c^T_j,i will describe all attainable methods by which y_j can have an effect on x_i. And in an effort to get that, we should always simply flip the concatenation diagram:

In fact, this interpretation may be generalized on transposing the product of a number of matrices:

[begin{equation*}
(ABC)^T = C^T B^T A^T
end{equation*}]

Why A^TA is at all times symmetrical, for any matrix A

A symmetrical matrix ‘S‘ is such an nxn sq. matrix, the place for any indexes i, j ∈ [1..n], we now have ‘s_i,j = s_j,i‘. Which means that it’s symmetrical upon its diagonal, in addition to that transposing it would don’t have any impact.

We see that transposing a symmetrical matrix can have no impact. So, a matrix ‘S‘ is symmetrical if and provided that:

[begin{equation*}
S^T = S
end{equation*}]

Equally, the X-diagram of a symmetrical matrix ‘S‘ has the property that it isn’t modified after a horizontal flip. That’s as a result of for any arrow s_i,j we now have an equal arrow s_j,i there:

In matrix evaluation, we now have a method stating that for any matrix ‘A‘ (not essentially symmetrical), the product A^TA is at all times a symmetrical matrix. In different phrases:

[begin{equation*}
(A^T A)^T = A^T A
end{equation*}]

It isn’t simple to really feel the correctness of this method if taking a look at matrix multiplication within the conventional approach. However its correctness turns into apparent if taking a look at matrix multiplication because the concatenation of their X-diagrams:

What’s going to occur if an arbitrary matrix ‘A‘ is concatenated with its horizontal flip A^T? The outcome A^TA might be symmetrical, as after a horizontal flip, the correct issue ‘A‘ involves the left facet and is flipped, turning into A^T, whereas the left issue A^T involves the correct facet and can also be flipped, turning into ‘A‘.

That is why for any matrix ‘A‘, the product A^TA is at all times symmetrical.

Understanding why (y, Ax) = (x, A^Ty)

There’s one other method in matrix evaluation, stating that:

[begin{equation*}
(y, Ax) = (x, A^T y)
end{equation*}]

the place “(u, v)” is the dot product of vectors ‘u‘ and ‘v‘:

[begin{equation*}
(u,v) = u_1 v_1 + u_2 v_2 + dots + u_n v_n
end{equation*}]

The dot product may be calculated just for vectors of equal size. Additionally, the dot product shouldn’t be a vector however a single quantity. If making an attempt as an instance the dot product “(u, v)” in a approach much like X-diagrams, we will draw one thing like this:

Now, what does the expression (y, Ax) really imply? It’s the dot product of vector ‘y‘ by the vector “Ax” (or by vector ‘x‘, which went by the transformation of “A“). For the expression (y, Ax) to make sense, we should always have:

|x| = columns(A), and
|y| = rows(A).

At first, let’s calculate (y, Ax) formally. Right here, each worth y_i is multiplied by the i-th worth of the vector Ax, denoted right here as “(Ax)_i“:

[begin{equation*}
(Ax)_i = a_{i,1}x_1 + a_{i,2}x_2 + dots + a_{i,m}x_m
end{equation*}]

After one multiplication, we can have:

[begin{equation*}
y_i(Ax)_i = y_i a_{i,1}x_1 + y_i a_{i,2}x_2 + dots + y_i a_{i,m}x_m
end{equation*}]

And after summing all of the phrases by “i ∈ [1, n]”, we can have:

[begin{equation*}
begin{split}
(y, Ax) = y_1(Ax)_1 + y_2(Ax)_2 + dots + y_n(Ax)_n =
= y_1 a_{1,1}x_1 + y_1 a_{1,2}x_2 + &dots + y_1 a_{1,m}x_m +
+ y_2 a_{2,1}x_1 + y_2 a_{2,2}x_2 + &dots + y_2 a_{2,m}x_m +
&vdots
+ y_n a_{n,1}x_1 + y_n a_{n,2}x_2 + &dots + y_n a_{n,m}x_m
end{split}
end{equation*}]

which clearly exhibits that within the product (y, Ax), each cell a_i,j of the matrix “A” participates precisely as soon as, along with the elements y_i and x_j.

Now let’s transfer to X-diagrams. If we wish to draw one thing like an X-diagram of vector “Ax“, we will do it within the following approach:

Subsequent, if we wish to draw the dot product (y, Ax), we will do it this fashion:

On this diagram, let’s see what number of methods there are to achieve the left endpoint from the correct one. The trail from proper to left can go by any arrow of A‘s X-diagram. If passing by a sure arrow a_i,j, it is going to be the trail composed of x_j, the arrow a_i,j, and y_i.

And this precisely matches the formal habits of (y, Ax) derived a bit above, the place (y, Ax) was the sum of all triples of the shape “y_i*a_i,j*x_j“. And we will conclude right here that if taking a look at (y, Ax) within the X-interpretation, it is the same as the sum of all attainable paths from the correct endpoint to the left one.

Now, what’s going to occur if we flip this complete diagram horizontally?

From the algebraic perspective, the sum of all paths from proper to left won’t change, as all collaborating phrases stay the identical. However wanting from the geometrical perspective, the vector ‘y‘ goes to the correct half, the vector ‘x‘ involves the left half, and the matrix “A” is being flipped horizontally; in different phrases, “A” is transposed. So the flipped X-diagram corresponds to the dot product of vectors “x” and “A^Ty” now, or has the worth of (x, A^Ty). We see that each (y, Ax) and (x, A^Ty) signify the identical sum, which proves that:

[begin{equation*}
(y, Ax) = (x, A^T y)
end{equation*}]

Conclusion

That’s all I needed to current in regard to the matrix transpose operation. I hope that the visible strategies illustrated above will assist all of us to realize a greater grasp of varied matrix operations.

Within the subsequent (and doubtless the final) story of this collection, I’ll handle inverting matrices, and the way it may be visualized by X-interpretation. We are going to see why formulation like “(AB)^-1 = B^-1A^-1” are the way in which they really are, and we are going to observe how the inverse works on a number of particular kinds of matrices.

So see you within the subsequent story!

My gratitude to:

– Asya Papyan, for the exact design of all of the used illustrations (linkedin.com/in/asya-papyan-b0a1b0243/),
– Roza Galstyan, for cautious evaluate of the draft (linkedin.com/in/roza-galstyan-a54a8b352/).

For those who loved studying this story, be at liberty to observe me on LinkedIn, the place, amongst different issues, I will even publish updates (linkedin.com/in/tigran-hayrapetyan-cs/).

All used pictures, except in any other case famous, are designed by request of the writer.

References

[1] – Understanding matrices | Half 1: matrix-vector multiplication – https://towardsdatascience.com/understanding-matrices-part-1-matrix-vector-multiplication/

[2] – Understanding matrices | Half 2: matrix-matrix multiplication – https://towardsdatascience.com/understanding-matrices-part-2-matrix-matrix-multiplication/