Perceive what Markov Determination Processes are and why they’re the muse of each Reinforcement Studying downside
I’ve talked about MDP (Markov Determination Course of) a number of instances, and it often seems in RL. However what precisely is an MDP, and why is it so essential in RL?
We’ll discover that collectively on this article! However first, in case you’re new to RL and need to perceive its fundamentals, try The Building Blocks of RL.
The Markov Property is an assumption that the prediction of the following state and reward relies upon solely on the present state and motion, not on the total historical past of previous states and actions. That is also referred to as the independence of path, which means your entire historical past(path) does not affect the transition and reward chances; solely the current issues. To formalize this assumption, we use conditional chance to point out that the prediction stays the identical whether or not or not we embrace earlier states and actions. If the brand new state and reward are impartial of the historical past given the present state and motion, their conditional chances stay unchanged.
Predicting subsequent state sₜ₊₁ and subsequent reward rₜ₊₁ given present state sₜ and present motion aₜ is equal to predicting subsequent state sₜ₊₁ and subsequent reward rₜ₊₁ given your entire historical past of states and actions as much as t.
This merely implies that having the historical past of earlier states and actions received’t have an effect on the chance; it’s impartial of it. In different phrases:
The longer term is impartial of the previous, given the current.
To fulfill the Markov property, the state should retain all related info wanted to make choices. In different phrases, the state must be an entire abstract of the atmosphere’s standing.
However will we all the time need to observe this assumption strictly?
Not essentially, in many real-world conditions, the atmosphere is partially observable, and the present state could not totally seize all the data wanted for optimum choices. Nonetheless, it’s widespread to approximate the Markov property when designing reinforcement studying options. This lets us mannequin the issue as a Markov Determination Course of (MDP), which is mathematically handy and broadly supported.
Nonetheless, when the Markov assumption isn’t applicable, different methods can assist the agent make higher choices.
An RL process that satisfies the Markov property known as a Markov Determination Course of (MDP). A lot of the core concepts behind MDPs are issues we’ve already talked about; it’s merely a proper method to mannequin an RL downside.
You possibly can consider it as:
- Surroundings (Drawback)
- Agent (Answer)
We’ve already mentioned this informally within the RL framework, however now let’s outline it formally!
MDP is a five-tuple:
State House.
S =
A = Motion House.
P = The chance of transitioning to the following state sₜ₊₁ given the present state sₜ and the present motion aₜ.
R = The anticipated rapid reward rₜ₊₁ given the present state sₜ, the present motion aₜ, and the following state sₜ₊₁
γ = low cost issue
State area and actions are carefully associated ideas already defined earlier; check with the primary a part of How Does an RL Agent Actually Decide What to Do? One essential notice: actions are thought of a part of the agent, not the atmosphere. Though an MDP is a proper mannequin of the atmosphere, it defines what actions can be carried out inside that atmosphere. Nonetheless, it’s the agent that’s accountable for selecting and executing these actions.
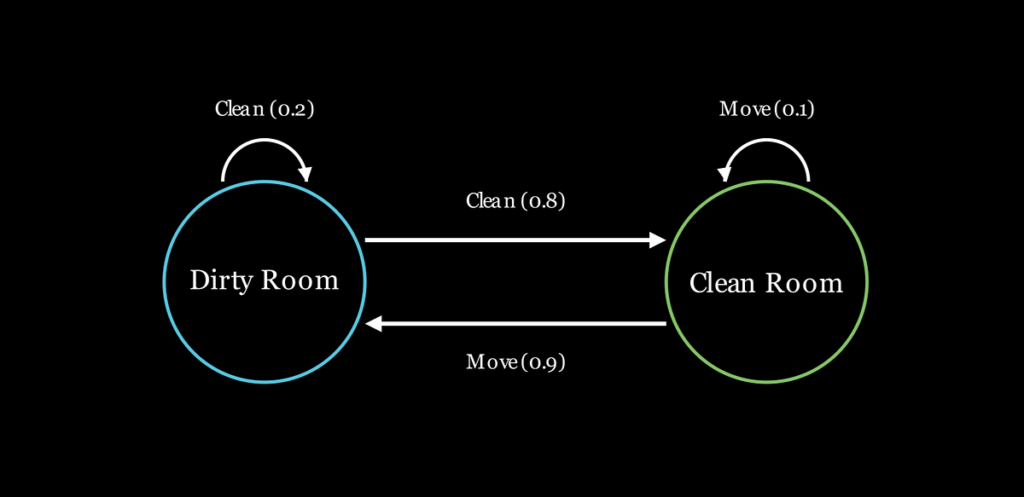
Keep in mind after we talked about that the atmosphere has transition dynamics? This refers to how transitions between states happen. Generally, even when we carry out the similar motion within the similar state, the atmosphere would possibly transition us to completely different subsequent states. Such an atmosphere known as stochastic. Our maze example’s atmosphere is deterministic as a result of each subsequent state is totally decided by the present state and motion.
Deterministic atmosphere: The identical motion in the identical state all the time results in the identical subsequent state and reward.
Stochastic atmosphere: The identical motion in the identical state can result in completely different subsequent states or rewards, primarily based on chances.
The identical idea applies to rewards: they may also be stochastic. Which means performing the identical motion in the identical state can produce completely different rewards.
Why will we use chances for transitions however anticipated values for rewards, though each are thought of stochastic? Just because we’re answering two completely different questions:
- For transitions: The place will I land subsequent?
- For Rewards: How a lot reward can I anticipate to get on common if this transition occurs (given the present state and motion)?
Transitions are occasions with related chances, whereas rewards are real-valued numbers.
Lastly, the low cost issue γ is the one addition we make to the MDP definition on this framework. It determines how future rewards are valued relative to rapid rewards and can be used later after we talk about the answer.