GitHub Repository: https://github.com/NavnoorBawa/Volatility-Surface-Anomaly-Detection-Trading-System
Disclaimer: This challenge is solely academic. No a part of this text constitutes monetary or funding recommendation. The methods mentioned are demonstrated for academic functions solely.
Constructing on my earlier work in volatility floor evaluation, I’ve carried out important enhancements to enhance detection accuracy and buying and selling sign technology. This text particulars the technical enhancements to my volatility floor anomaly detection system, specializing in superior machine studying architectures, differential studying methods, and adaptive sensitivity frameworks that present extra dependable buying and selling alerts.
The improved system now options LSTM/GRU networks, superior volatility fashions, and improved sign confidence scoring. These enhancements permit for extra nuanced evaluation of market inefficiencies in choices pricing.
I’ve carried out three distinct mannequin architectures, every with particular benefits:
def _build_model(self):
# Enter layer
input_layer = Enter(form=self.input_shape, title="vol_surface_input")# Reshape for sequence fashions
x = Reshape((self.input_shape[0], self.input_shape[1]))(input_layer)
# Bidirectional LSTM layers
x = Bidirectional(LSTM(64, return_sequences=True))(x)
x = Bidirectional(LSTM(32))(x)
# Dense encoding layers
encoded = Dense(self.encoding_dim, activation='relu', title="bottleneck")(x)
# Decoding layers
x = Dense(self.input_shape[0] * self.input_shape[1] // 2, activation='relu')(encoded)
x = Dense(self.input_shape[0] * self.input_shape[1], activation='sigmoid')(x)
# Reshape again to authentic dimensions
decoded = Reshape((self.input_shape[0], self.input_shape[1], 1))(x)
# Create mannequin
self.mannequin = Mannequin(input_layer, decoded, title="VolSurfaceLSTM")
- LSTM/GRU Networks: Superior for capturing temporal dependencies throughout choice maturities
- Traditional Autoencoders: Balanced performance-to-speed ratio for speedy evaluation
- Hybrid CNN-LSTM: Highest accuracy for detecting delicate market inefficiencies
The bidirectional LSTM structure considerably improves the system’s capability to detect patterns throughout each the strike and maturity dimensions concurrently.
Impressed by current analysis in quantitative finance, I’ve carried out differential machine studying that trains on each worth ranges and their gradients:
def train_with_differentials(self, vol_surface, compute_gradients=True):
# Create augmented dataset
training_surfaces = self._create_augmented_dataset(vol_surface)# Compute differentials (gradients) of the floor
if compute_gradients:
# Calculate strike gradients
strike_gradients = np.zeros_like(training_surfaces)
for i in vary(len(training_surfaces)):
strike_gradients[i, :, :-1, 0] = np.diff(training_surfaces[i, :, :, 0], axis=1)
# Calculate maturity gradients
maturity_gradients = np.zeros_like(training_surfaces)
for i in vary(len(training_surfaces)):
maturity_gradients[i, :-1, :, 0] = np.diff(training_surfaces[i, :, :, 0], axis=0)
# Create multi-output mannequin
dml_model = Mannequin(input_layer,
[surface_output, strike_grad_output, maturity_grad_output])
dml_model.compile(optimizer=Adam(learning_rate=self.learning_rate),
loss=['mse', 'mse', 'mse'],
loss_weights=[1.0, 0.5, 0.5])
This method gives:
- Extra correct calibration of stochastic volatility fashions
- Higher preservation of native volatility construction
- Diminished overfitting to market noise
A key innovation is the implementation of a dynamic sensitivity framework that adapts to market situations:
def tune_anomaly_sensitivity(self, vol_surface, market_conditions=None, sensitivity_level='medium'):
# Map sensitivity degree to numerical parameters
sensitivity_map = {
'low': {'percentile': 95, 'threshold_multiplier': 2.0, 'std_deviations': 2.0},
'medium': {'percentile': 90, 'threshold_multiplier': 1.5, 'std_deviations': 1.5},
'excessive': {'percentile': 85, 'threshold_multiplier': 1.2, 'std_deviations': 1.0}
}# Get base settings from sensitivity degree
settings = sensitivity_map.get(sensitivity_level, sensitivity_map['medium'])
# Calculate volatility floor metrics
vol_mean = np.imply(vol_surface)
vol_std = np.std(vol_surface)
vol_skew = np.imply(((vol_surface - vol_mean) / vol_std) ** 3) if vol_std > 0 else 0
# Adapt sensitivity based mostly on floor traits
adaptive_multiplier = 1.0
# Enhance sensitivity for extra risky surfaces
if vol_std > 0.1:
adaptive_multiplier *= 0.9
# Enhance sensitivity for skewed surfaces
if abs(vol_skew) > 0.5:
adaptive_multiplier *= 0.85
The framework dynamically adjusts detection thresholds based mostly on:
- Present volatility ranges
- Skew magnitude
- Time period construction traits
- Consumer-defined danger tolerance (low/medium/excessive)
This adaptive method considerably reduces false positives whereas nonetheless capturing real buying and selling alternatives.
The system now employs a extra subtle market regime classification system:
def classify_market_regime(self, vol_surface):
if self.regime_classifier is None:
# Calculate key floor traits
vol_mean = np.imply(vol_surface)
vol_std = np.std(vol_surface)# Calculate moneyness and time period construction results
center_idx = vol_surface.form[1] // 2
left_side = vol_surface[:, :center_idx]
right_side = vol_surface[:, center_idx:]
skew = np.imply(left_side) - np.imply(right_side)
# Calculate time period construction
if vol_surface.form[0] > 1:
short_term = vol_surface[0, :]
long_term = vol_surface[-1, :]
term_structure = np.imply(long_term) - np.imply(short_term)
# Decide regime based mostly on traits
if vol_mean < 0.15:
regime = 'low_volatility'
confidence = 0.7
elif vol_mean > 0.3:
regime = 'high_volatility'
confidence = 0.8
elif abs(skew) > 0.05:
regime = 'skewed'
confidence = 0.6 + min(0.3, abs(skew))
elif abs(term_structure) > 0.03:
regime = 'volatile_term_structure'
confidence = 0.6 + min(0.3, abs(term_structure))
The classification now identifies eight distinct market regimes with confidence scores:
- Low Volatility
- Excessive Volatility
- Regular
- Skewed
- Unstable Time period Construction
- Excessive Skew Excessive Vol
- Low Skew Low Vol
- Flat Time period Construction
Every regime has particular subtypes for extra granular classification (e.g., “disaster”, “negative_tail_risk”).
I’ve carried out extra subtle volatility fashions past Black-Scholes:
def rough_bergomi_price(self, S, Ok, T, r, H, nu, rho, option_type='name', n_paths=10000):
"""
Tough Bergomi mannequin for pricing with fractional Brownian movement
"""
dt = T / 100 # Time step dimension
instances = np.arange(0, T + dt, dt)
n_steps = len(instances) - 1# Simulate fractional Brownian paths
dW1 = np.random.regular(0, np.sqrt(dt), (n_paths, n_steps))
dW2 = np.random.regular(0, np.sqrt(dt), (n_paths, n_steps))
# Create correlated Brownian motions
dB = rho * dW1 + np.sqrt(1 - rho**2) * dW2
# Initialize arrays
S_paths = np.zeros((n_paths, n_steps + 1))
V_paths = np.zeros((n_paths, n_steps + 1))
# Set preliminary values
S_paths[:, 0] = S
V_paths[:, 0] = nu
# Simulate paths with tough volatility dynamics
for i in vary(n_steps):
V_paths[:, i + 1] = V_paths[:, i] * np.exp(
-0.5 * V_paths[:, i] * dt + np.sqrt(V_paths[:, i]) * dW1[:, i]
)
S_paths[:, i + 1] = S_paths[:, i] * np.exp(
(r - 0.5 * V_paths[:, i]) * dt + np.sqrt(V_paths[:, i]) * dB[:, i]
)
- Tough Bergomi Mannequin: Higher captures high-frequency volatility dynamics with fractional Brownian movement
- Bounce Diffusion Mannequin: Accounts for market jumps and tail occasions
- Black-Scholes Mannequin: Customary mannequin used as a baseline
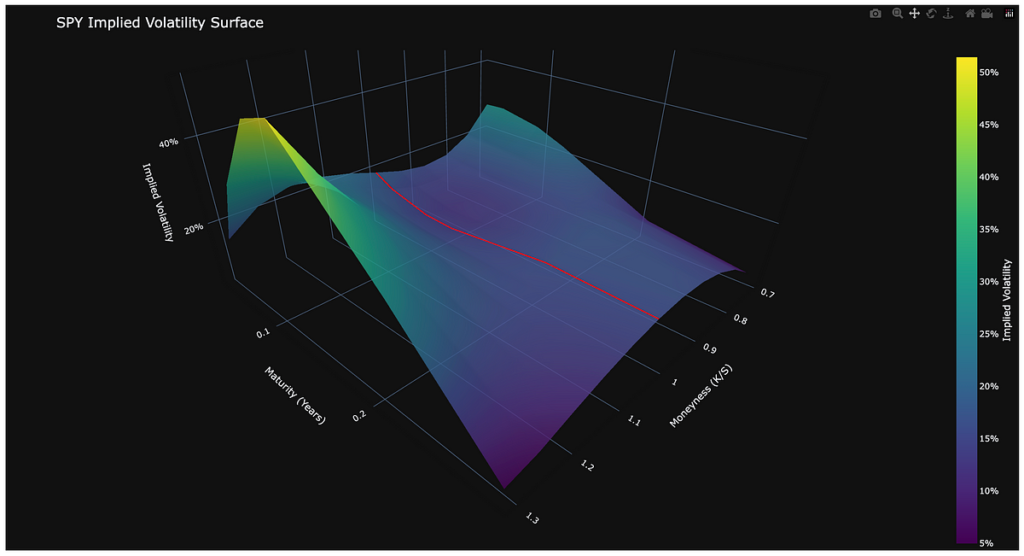
Working the improved system on SPY choices with excessive sensitivity parameters produced detailed evaluation: