Anomaly Detection in Sequential Data using LSTM Autoencoder and KMeans Clustering (unsupervised) | by Falonne KPAMEGAN | Jun, 2025

Let’s visualize our information :

import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
plt.determine(figsize=(12,6))
sns.lineplot(x=df.index, y=df['value'])
plt.present()

sns.histplot(df['value'], bins=100, kde=True)

After verifying information are properly formated, we normalized the time collection utilizing MinMaxScaler and generated overlapping home windows of mounted size (SEQ_LENGTH) to feed into the LSTM.

scaler = MinMaxScaler()
scaled_data = scaler.fit_transform(df[['value']])
def create_sequences(information, seq_length):
X = []
for i in vary(len(information) - seq_length):
X.append(information[i:i + seq_length])
return np.array(X)
SEQ_LENGTH = 50
X = create_sequences(scaled_data, SEQ_LENGTH)

input_dim = X.form[2]
timesteps = X.form[1]
inputs = Enter(form=(timesteps, input_dim))
encoded = LSTM(64, activation='relu', return_sequences=False, title="encoder")(inputs)
decoded = RepeatVector(timesteps)(encoded)
decoded = LSTM(64, activation='relu', return_sequences=True)(decoded)
autoencoder = Mannequin(inputs, decoded)
autoencoder.compile(optimizer='adam', loss='mse')
autoencoder.match(X, X, epochs=50, batch_size=64, validation_split=0.1, shuffle=True)

To entry the latent illustration, we outline a seperate encoder mannequin:

encoder_model = Mannequin(inputs, encoded)
latent_vectors = encoder_model.predict(X, verbose=1, batch_size=32)  # form = (num_samples, 64)

Fairly than thresholding reconstruction errors, we apply KMeans clustering to the compressed latent vectors:

from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=2, random_state=42)
labels = kmeans.fit_predict(latent_vectors)
# We assume the bigger cluster is "regular"
normal_cluster = np.bincount(labels).argmax()
anomaly_mask = labels != normal_cluster

We visualize the latent house with PCA

from sklearn.decomposition import PCA
pca = PCA(n_components=2)
latent_pca = pca.fit_transform(latent_vectors)
plt.determine(figsize=(10, 6))
sns.scatterplot(x=latent_pca[:, 0], y=latent_pca[:, 1], hue=labels, palette='Set1', s=50, alpha=0.7)
plt.title("Kmeans cluster in latent house (PCA 2D)")
plt.xlabel("principal element 1")
plt.ylabel("principal element 2")
plt.grid(True)
plt.present()

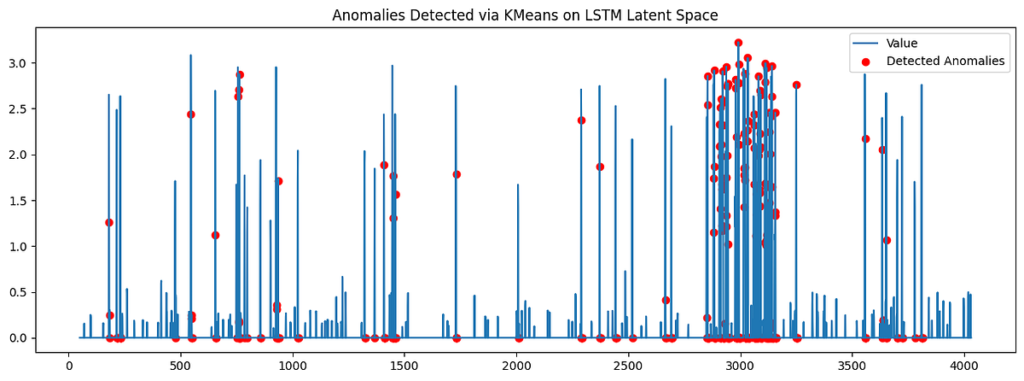
timestamps = balancer.index[SEQ_LENGTH:]
plt.determine(figsize=(15, 5))
plt.plot(timestamps, df['value'][SEQ_LENGTH:], label='Worth')
plt.scatter(timestamps[anomaly_mask], df['value'][SEQ_LENGTH:][anomaly_mask], shade='pink', label='Detected Anomalies')
plt.legend()
plt.title("Anomalies Detected through KMeans on LSTM Latent House")
plt.present()

By combining the sequence modeling capabilities of LSTM Autoencoders with the unsupervised grouping of KMeans, we had been in a position to successfully detect anomalies in time collection information — even with out labeled anomalies.

This strategy is highly effective as a result of:

• It doesn’t require labeled coaching information.
• It adapts to advanced sequential patterns.
• It permits latent house exploration for clustering and visualization.

Thanks for studying, I hope it’s helpful !