How a novel method permits compact fashions to rival giants like OpenAI’s o1 via strategic “deep pondering.”
On this publish, we are going to go over a paper known as “rStar-Math: Small LLMs Can Grasp Math Reasoning with Self-Advanced Deep Considering”, which may rival and even surpass the mathematics reasoning functionality of OpenAI o1 with out distillation from superior fashions.
In a time when large AI fashions like GPT-4 are sometimes within the information, this paper questions the concept that bigger fashions are mechanically higher. It presents a brand new means for smaller language fashions (SLMs) to compete with, and even outperform, giant fashions like OpenAI’s o1, with no need costly coaching strategies. Let’s take a better take a look at how this workforce got here up with new methods to unravel issues for smaller fashions.
Giant language fashions (LLMs) are nice at fixing complicated issues, however they’re costly to run and never straightforward to entry for on a regular basis use. Smaller fashions have two primary points. First, their coaching information usually comprises refined errors. Many math datasets come from bigger fashions, which typically make errors of their steps. It’s like a pupil copying homework from a trainer who makes slight errors. These errors can add up and lead the coed within the mistaken course. Second, smaller fashions often take a “one-shot” method to fixing issues, much like fast, instinctive pondering. Whereas this may be quick, it doesn’t work properly for sophisticated issues that want cautious pondering and step-by-step reasoning. It’s like a pupil shortly writing a solution with out checking it, which may result in errors. This led the rStar-Math workforce to ask an necessary query: Can smaller fashions study to suppose extra deeply, discover totally different options, and repair their errors on their very own with no need a number of human assist or computing energy?
The reply lies in three synergistic improvements, mixing code execution, strategic choice studying, and a search algorithm borrowed from recreation concept.
- Code-Augmented Verification: No Extra Fortunate Guesses
Each reasoning step is paired with executable code (e.g., Python or SymPy snippets). For example, when fixing `2x + 4 = 10`, the mannequin doesn’t simply write “Subtract 4 from either side” — it generates:
# Step 1: Subtract 4 from either side
2x = 10–4 # Executing this code verifies 2x = 6
Solely steps with error-free code survive, filtering out guesswork. This mirrors how a meticulous pupil checks every equation iteration with a calculator, guaranteeing no misstep goes unnoticed.
2. Course of Desire Mannequin (PPM): Instructing “Good Habits”
Even right steps may be suboptimal. The PPM acts like a seasoned tutor, rewarding strategies that align with long-term success. For instance, after simplifying to `2x = 6`, each “Divide by 2” and “Multiply by 0.5” are mathematically legitimate. Nevertheless, the PPM favors division — a extra intuitive and scalable technique for learners. This nudges the mannequin towards systematic reasoning, very like academics prioritize foundational methods over intelligent shortcuts.
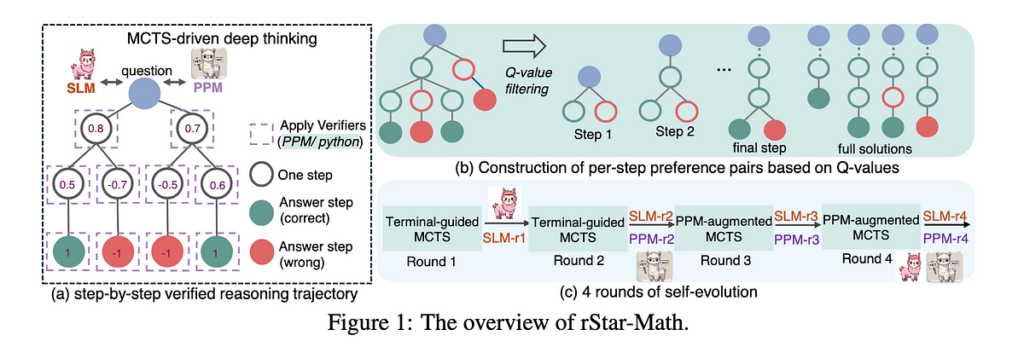
3. Self-Evolution through Monte Carlo Tree Search (MCTS): Studying By way of Exploration
Impressed by AlphaGo’s success, rStar-Math adapts MCTS — a decision-making algorithm that balances exploration and exploitation — for math issues. Right here’s the way it works in observe:
– Constructing the Tree: Beginning with a root downside (e.g., `2x + 4 = 10`), the mannequin generates a number of candidate actions (e.g., “Subtract 4,” “Divide by 2”). Every motion turns into a department.
– Simulating Outcomes: The algorithm explores paths, simulating options whereas the PPM evaluates every step’s high quality. Profitable paths (like fixing for `x = 3`) are strengthened, whereas dead-ends (e.g., incorrect “Subtract 2” steps) are deprioritized.
– Backpropagation: Insights from profitable simulations propagate backward, updating the tree to mirror which steps are most promising.
Instance Drawback: Remedy 2x+4=102x+4=10
Assume the coverage SLM generates 3 candidate steps (for simplicity) at every node, and we run 2 rollouts (iterations) for instance the method.
Rollout 1: First Exploration
1- Root Node (Step 0):
— Candidates:
- 2x+4=10→Subtract 42x+4=10→Subtract 4
- 2x+4=10→Divide by 22x+4=10→Divide by 2
- 2x+4=10→Guess x=32x+4=10→Guess x=3
2- Choice:
— The PPM and UCT method choose “Subtract 4” (highest preliminary rating).
3- Enlargement:
— Create a brand new node: Step 1 after subtracting 4: 2x=62x=6.
— Generate 3 new candidates for Step 1:
- 2x=6→Divide by 22x=6→Divide by 2
- 2x=6→Multiply by 0.52x=6→Multiply by 0.5
- 2x=6→Subtract 22x=6→Subtract 2 (incorrect step).
4- Simulation:
— Simulate from Step 1 (2x=62x=6) utilizing the coverage SLM:
- Choose “Divide by 2” → x=3x=3.
- Code execution verifies x=3x=3 is right.
5- Backpropagation:
— Replace scores for all nodes within the path:
- Root node (Step 0): Q-value will increase (because the path led to success).
- Step 1 node: Q-value will increase.
Rollout 2: Second Exploration
1- Root Node (Step 0):
— Candidates (now with up to date Q-values):
- “Subtract 4” (excessive rating from Rollout 1).
- “Divide by 2” (unexplored).
- “Guess x=3x=3″ (unexplored).
2- Choice:
— UCT balances exploration/exploitation. It picks “Divide by 2” (to discover a brand new path).
3- Enlargement:
— Create a brand new node: Step 1 after dividing by 2: x+2=5x+2=5.
— Generate 3 new candidates:
- x+2=5→Subtract 2x+2=5→Subtract 2
- x+2=5→Multiply by 1x+2=5→Multiply by 1 (redundant)
- x+2=5→Add 3x+2=5→Add 3 (incorrect).
4- Simulation:
— Simulate from Step 1 (x+2=5x+2=5):
- Choose “Subtract 2” → x=3x=3.
- Code execution verifies correctness.
5- Backpropagation:
— Replace scores for the brand new path:
- Root node (Step 0): Q-value for “Divide by 2” will increase.
- Step 1 node (new department): Q-value will increase.
Remaining Tree State
After 2 rollouts, the search tree seems to be like this:
Root (Step 0: 2x+4=10)
├── Path 1: Subtract 4 → Step 1 (2x=6) → x=3 (success)
└── Path 2: Divide by 2 → Step 1 (x+2=5) → x=3 (success)
Each paths result in the proper reply, however their Q-values differ primarily based on PPM rankings (e.g., “Subtract 4” may be most well-liked for readability).
The next is one other instance from the paper:
Coaching: From Bootstrap to Self-Evolution
The mannequin undergoes 4 evolutionary rounds:
1. Bootstrap: Preliminary coaching makes use of high-quality information from DeepSeek-Coder, a sturdy exterior mannequin.
2. Refinement Rounds: The mannequin tackles progressively more durable issues (e.g., Olympiad-level questions). MCTS generates improved options, which then prepare higher variations of the mannequin and PPM. This creates a virtuous cycle — higher information → higher fashions → higher information.
Outcomes: Punching Above Their Weight
– MATH Benchmark: A 7B-parameter mannequin achieved 90% accuracy, outperforming OpenAI’s o1-preview (85.5%).
– USA Math Olympiad (AIME): Solved 53.3% of issues, rivalling high highschool rivals.
– Self-Correction: The system developed an intrinsic capability to backtrack from errors, akin to a pupil realizing a miscalculation mid-problem.
Challenges and Future Horizons
Whereas promising, rStar-Math isn’t flawless. MCTS calls for heavy GPU assets, limiting accessibility. Geometry issues — reliant on visible/spatial reasoning — stay a hurdle, a lot as they do for people with out diagrams. Future work could discover integrating multimodal inputs or optimizing MCTS effectivity.
Conclusion: Smarter, Not Simply Larger
rStar-Math demonstrates that strategic design can elevate small fashions to elite efficiency. By emulating human-like deliberation — exploring a number of pathways, verifying steps, and studying from errors — it challenges the narrative that AI progress hinges on scale. This isn’t only a leap for math reasoning; it’s a blueprint for democratizing superior AI, proving that ingenuity can trump brute computational power.