Within the decision (ER), one of many central challenges is managing and sustaining the complicated relationships between data. At its core, Tilores fashions entities as graphs: every node represents a document, and edges characterize rule-based matches between these data. This method provides us flexibility, traceability, and a excessive stage of accuracy, however it additionally comes with vital storage and computational challenges, particularly at scale. This text explains the main points about effectively storing extremely related graphs utilizing clique-based graph Compression.
The Entity Graph Mannequin
In Tilores, a sound entity is a graph the place each document is related to no less than one different through an identical rule. For example, if document a matches document b in keeping with rule R1, we retailer that as an edge "a:b:R1". If one other rule, say R2, additionally connects a and b, we retailer an extra edge "a:b:R2". These edges are stored as a easy checklist, however may alternatively be modeled utilizing an adjacency checklist construction for extra environment friendly storage.
Why Retain All Edges?
Most Entity Resolution programs or grasp knowledge administration programs don’t retain the relationships between data, however solely retailer a illustration of the underlying knowledge and sometimes a generic matching rating, leaving the person unsure about how the entity was shaped. Even worse, the person has no method to appropriate errors made by the automated matching system.
Therefore, retaining all edges in an entity graph serves a number of functions:
- Traceability: Permits the person to grasp why two data had been grouped into the identical entity.
- Analytics: Insights similar to rule effectiveness and knowledge similarity may be extracted from edge metadata.
- Information Deletion & Recalculation: When a document is deleted or a rule is modified, the graph should be recalculated. Edge info is crucial to grasp how an entity was shaped and the way it needs to be up to date.
The Scaling Downside: Quadratic Development
When discussing potential scaling points in entity decision, this sometimes refers back to the problem of matching every document with all different data. Whereas this can be a challenge on its own, retaining all edges of an entity leads to related points on the storage facet. Entities the place many data are related with one another create a mess of edges. Within the worst case each new document is related to all current data. This quadratic progress may be expressed with the components:
n * (n - 1) / 2
For small entities, this isn’t a difficulty. For instance, an entity with 3 data can have a most of three edges. For n = 100, this will increase to 4,950 edges and for n = 1,000 this leads to as much as 499,500 edges.
This creates an immense storage and computational overhead, particularly since entity decision graphs typically exhibit this type of dense connectivity.
Answer: Clique-Based mostly Graph Compression (CBGC)
A clique in a graph is a gaggle of nodes the place each node is related to each different node in that group. A clique can be referred to as an entire subgraph. The smallest potential clique incorporates a single node and no edges. A pair of nodes related by an edge additionally varieties a clique. And three nodes, such because the one under, type a triangle formed clique.
(picture by the writer)
A maximal clique is a clique that can not be prolonged by including any adjoining node, and a most clique is the clique with the most important variety of nodes in the entire graph. For the aim of this text, we’re going to make use of the time period clique solely to check with cliques with no less than three nodes.
The beforehand proven triangle could possibly be represented in Tilores by the next edges:
[
"a:b:R1",
"a:c:R1",
"b:c:R1"
]As a result of a triangle is a clique, we may additionally characterize the graph by storing solely the nodes on this clique and the related rule ID:
{
"R1": [
["a", "b", "c"]
]
}Let’s think about the next barely extra difficult graph:

(picture by the writer)
Based mostly on its look, we will simply spot that every one nodes are related to one another. So as a substitute of itemizing all 15 edges [remember n*(n-1)/2], we will merely retailer this clique within the following type:
{
"R1":[
["a", "b", "c", "d", "e", "f"]
]
}Nevertheless, in a sensible graph, not all data are related to one another. Think about the next graph:

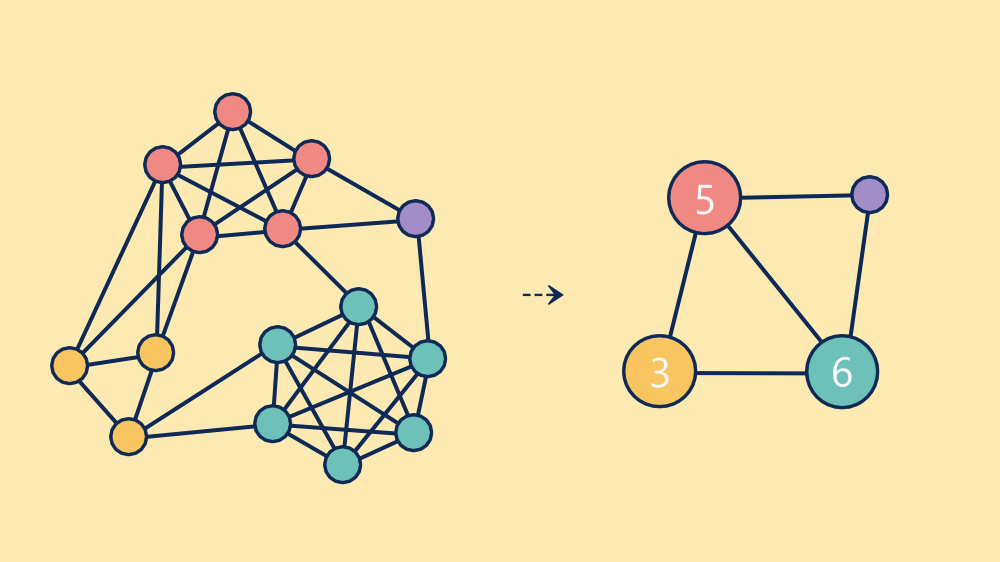
(picture by the writer)
There are three bigger cliques highlighted: yellow, purple and blue (teal if you happen to’re choosy). There may be additionally a single remaining node. Whereas these are in all probability the most important cliques, you would possibly spot dozens of others. For instance, do you discover the 4-node clique between the 2 purple and two yellow nodes?
Sticking with the coloured cliques, we may retailer them within the following approach (utilizing y, r and b for yellow, purple and blue):
{
"R1": [
["y1", "y2", "y3"],
["r1", "r2", "r3", "r4", "r5"],
["b1", "b2", "b3", "b4", "b5", "b6"]
]
}Moreover, we will retailer the remaining 10 edges (p for purple):
[
"y1:r1:R1",
"y1:r2:R1",
"y2:r1:R1",
"y2:r2:R1",
"r4:p1:R1",
"r5:p1:R1",
"r5:b1:R1",
"b2:p1:R1",
"y3:b5:R1",
"y3:b6:R1"
]Which means the entire graph can now be represented with solely three cliques and ten edges, as a substitute of the unique 38 edges.

(picture by the writer)
This clique-based graph compression (CBGC) is loss-free (except you want edge properties). In a sensible dataset, we recognized large storage financial savings. For one buyer, CBGC decreased edge storage by 99.7%, changing a whole lot of 1000’s of edges with only a few hundred cliques and sparse edges.
Efficiency Advantages Past Storage
CBGC is not only about compression. It additionally permits sooner operations, significantly when dealing with document and edge deletion.
Any sane entity decision engine ought to break up an entity into a number of ones if the one hyperlink between two subgraphs was deleted, for instance, because of regulatory or compliance causes. Figuring out separate, unconnected subgraphs is often executed utilizing a related elements algorithm. In brief, it really works by grouping all nodes which might be related through edges into separate subgraphs. Because of this every edge must be checked no less than as soon as.
Nevertheless, if a graph is saved as a compressed graph, then there isn’t a have to traverse all edges of a clique. As an alternative it’s adequate so as to add a restricted variety of edges for every clique, for instance a transitive path between the nodes of a clique, treating every clique as a pre-connected subgraph.
Commerce-Offs: Clique Detection Complexity
There’s a trade-off: clique detection is computationally costly, significantly when searching for the utmost cliques, a well known NP-hard drawback.
In follow it’s typically adequate to simplify this workload. Approximate algorithms for clique detection (e.g. grasping heuristics) carry out nicely sufficient for many makes use of. Moreover, CBGC is recalculated selectively, normally when an entity’s edge rely surpasses a threshold. This hybrid method balances compression effectivity with acceptable processing price.
Past Cliques
Arguably, the most typical sample in entity decision is the entire subgraph. Nevertheless, additional optimization could possibly be achieved by figuring out different recurring patterns similar to
- stars: retailer as an inventory of nodes the place the primary entry represents the central node
- paths: retailer as an ordered checklist of nodes
- communities: retailer like a clique and mark the lacking edges
Closing Ideas
Entity decision programs typically face the problem of managing dense, extremely interconnected graphs. Storing all edges naively shortly turns into unsustainable. CBGC supplies an environment friendly method to mannequin entities by exploiting structural properties of the information.
Not solely does it scale back storage overhead, however it additionally improves system efficiency, particularly throughout knowledge deletion and reprocessing. Whereas clique detection has its computational prices, cautious engineering selections permit us to reap the advantages with out sacrificing scalability.