En Yakın Komşu Algoritmaları (KNN Search Algorithms) | by Beyza Öztürk | Apr, 2025

Makine öğreniminde ve özellikle sınıflandırma/regresyon gibi denetimli öğrenme problemlerinde, en yakın komşuların (nearest neighbors) hızlı ve verimli şekilde bulunması oldukça kritiktir. Aşağıda kullanılan iki temel yöntem açıklanmıştır:

Kaba Kuvvet Yöntemi (Brute Drive Technique)

Tanım:
Kaba kuvvet yaklaşımı, veri kümesindeki her bir nokta çifti arasındaki mesafeyi doğrudan hesaplar. En saf ve doğrudan yöntemdir.

Özellikleri:

• Basittir: Her veri noktası diğer tüm noktalarla tek tek karşılaştırılır.
• Doğruluğu yüksektir, ancak hesaplama maliyeti çok fazladır.
• Küçük veri setlerinde oldukça etkilidir.

Zorluklar:

• Veri seti büyüdükçe (özellikle yüksek boyutlu ve çok örnekli veri setlerinde), işlem sayısı O(n²) ölçeğinde büyür.
• Bu nedenle büyük veri setlerinde uygulanabilirliği zayıflar.

KD Ağacı (KDTree)

Tanım:
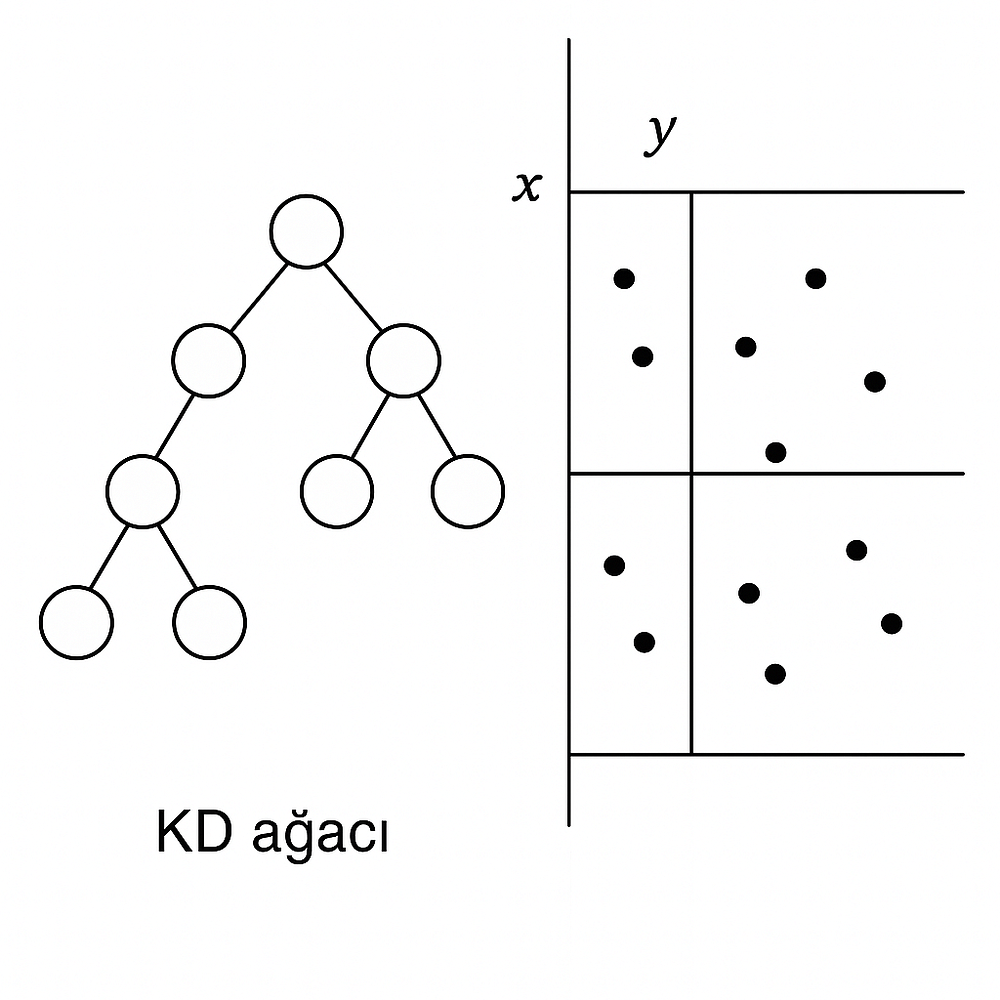
KD Ağacı (Ok-Dimensional Tree), veri kümesini uzayda eksenlere göre bölerek verilerin yerleştirildiği ikili bir ağaç yapısıdır. Bu yapı, daha az sayıda mesafe hesaplaması yaparak komşu aramasını hızlandırır.

Nasıl Çalışır:

• Uzay, her adımda bir eksen boyunca ikiye bölünür.
• Bu şekilde veri kümesi küçük alt bölgelere ayrılır (ortotropik bölgelere).
• Bir sorgu noktası için en yakın komşu aranırken, yalnızca ilgili bölgelerdeki noktalar kontrol edilir. Uzak bölgeler tamamen atlanabilir.

Avantajları:

• Kaba kuvvete göre çok daha hızlıdır.
• Özellikle düşük boyutlu veri setleri için çok etkilidir.

Dezavantajları:

• Boyut sayısı arttıkça (curse of dimensionality) performansı düşer.
• 20+ boyuttan sonra brute-force ile benzer hızlara düşebilir.

High Ağacı (Ball Tree)

High Ağacı, özellikle yüksek boyutlu veri kümeleri için geliştirilmiş bir verimli komşu arama algoritmasıdır. KD ağaçlarının sınırlamalarını aşmak üzere tasarlanmıştır.

🔹 Temel Fikir

• KD Ağaçları veriyi eksenlere göre bölerken, High Ağaçları veriyi hiper küreler (balls) içinde bölerek hiyerarşik bir yapı oluşturur.
• Her düğüm (node) bir veri kümesini temsil eder ve bu küme:
• Bir merkez nokta (centroid)
• Ve bir yarıçap (radius) ile tanımlanan hiper kürenin (n-boyutlu küre) içinde yer alır.
• Böylece veri kümesi iç içe geçen toplar (hiper küreler) halinde set up edilir.

🔹 Komşu Aramada Nasıl Çalışır?

1. Bir take a look at noktası için, ilk olarak ağacın kök düğümündeki topun merkeziyle olan mesafesi hesaplanır.
2. Üçgen eşitsizliği kullanılarak, o düğümün (veya alt düğümlerinin) içinde yer alan noktalarla olan olası en küçük ve en büyük mesafeler tahmin edilir.
3. Eğer bu tahmini mesafe, mevcut en yakın komşudan daha büyükse, düğüm atlanabilir (bu, hesaplamaları azaltır).
4. Böylece yalnızca gerçekten gerekli bölgelerde mesafe hesaplaması yapılır.

🔸 Dezavantajları

• İnşa süresi, KD ağacından daha maliyetlidir çünkü her düğüm için hiper küre hesaplamaları yapılır.
• Düşük boyutlu ve az örnekli verilerde, KDTree veya brute-force daha pratik olabilir.

🔍 En Uygun Komşu Algoritmasının Seçimi

Veri kümesine göre brute, kd_tree, ball_tree gibi algoritmalar arasında seçim yapmak için birçok faktör göz önünde bulundurulmalıdır:

🧭 2. Veri Yapısı (İçsel Boyutluluk ve Seyreklik)

• İçsel boyutluluk: Verinin gerçekten yaşadığı alt uzayın boyutu.
• Düşük içsel boyutluluk = daha iyi ağaç performansı
• Seyreklik: Verinin uzaydaki yayılım derecesi
• Seyrek ve yapılandırılmış veri = ağaçlar daha hızlı çalışır

🔁 Brute power, veri yapısından etkilenmez; tüm mesafeleri tek tek hesaplar.
🌲 Ağaç tabanlı yöntemler, veri yapısına çok duyarlıdır.

Ağaçlarda ok büyüdükçe:

• Daha geniş arama yapılması gerekir.
• Öncelikli kuyruk (precedence queue) işlemleri maliyetli hale gelir.
• Budama etkisi azalır → brute power bazen daha iyi olur.

• KDTree/BallTree için önce yapılandırma (ağaç oluşturma) gerekir.
• Sadece birkaç sorgu yapılacaksa, bu yapılandırma maliyetlidir.

🛠️ 5. Scikit-learn Otomatik Seçim (algorithm='auto')

Scikit-learn, aşağıdaki koşullarda otomatik olarak brute kullanır:

1. Giriş verisi seyrek (sparse) matris ise
2. metric='precomputed' kullanılmışsa
3. Belirtilen metrik, kd_tree veya ball_tree‘nin desteklemediği türdeyse

Aksi durumda:

• Önce kd_tree denenir.
• Eğer uygun değilse ball_tree kullanılır.

🔍 Bu seçim, varsayılan olarak sorgu sayısının büyük, leaf_size ≈ 30 ve verilerin düşük boyutlu olduğu varsayımına dayanır.

💡 Özet Seçim Kriteri Tablosu

🌿 leaf_size Parametresi Nedir?

leaf_size, KDTree ve BallTree algoritmalarında bir yaprak düğümde bulunabilecek maksimum örnek sayısını belirler.

🎯 Neden Önemlidir?

Yaprak düğüm boyutu, hem inşaat süresi, hem sorgu süresi, hem de hafıza tüketimi üzerinde önemli etkilere sahiptir.

🧱 1. Ağaç Oluşturma Zamanı

• Daha büyük leaf_size → daha az düğüm, daha kısa inşa süresi
• Küçük leaf_size → daha çok düğüm, daha karmaşık yapı → daha uzun süre

⏱️ 2. Sorgu Zamanı

💾 3. Hafıza Kullanımı

• Daha büyük leaf_size → daha az düğüm → daha az merkez ve yarıçap bilgisi
• Özellikle BallTree yapısında, her düğüm bir d-d boyutlu merkez vektörü saklar.
• Hafıza gereksinimi yaklaşık:

from sklearn.neighbors import KDTree
print(sorted(KDTree.valid_metrics))

️ Önemli Notlar

• "cosine" metriği genellikle cosine_distances fonksiyonuyla uygulanır.
• Bazı metrikler yalnızca kaba kuvvet ile desteklenir (örneğin hamming, jaccard, vs.)

KAYNAK:

https://scikit-learn.org/stable/modules/neighbors.html#nearest-neighbors-regression