On this article, I’ll introduce you to hierarchical Bayesian (HB) modelling, a versatile strategy to routinely mix the outcomes of a number of sub-models. This technique allows estimation of individual-level results by optimally combining info throughout completely different groupings of information by means of Bayesian updating. That is significantly precious when particular person items have restricted observations however share frequent traits/behaviors with different items.
The next sections will introduce the idea, implementation, and different use instances for this technique.
The Drawback with Conventional Approaches
As an software, think about that we’re a big grocery retailer attempting to maximise product-level income by setting costs. We would want to estimate the demand curve (elasticity) for every product, then optimize some revenue maximization operate. As step one to this workstream, we would want to estimate the worth elasticity of demand (how responsive demand is to a 1% change in worth) given some longitudinal knowledge with $i in N$ merchandise over $t in T$ intervals. Keep in mind that the worth elasticity of demand is outlined as:
$$beta=frac{partial log{textrm{Items}}_{it}}{partial log textrm{Worth}_{it}}$$
Assuming no confounders, we are able to use a log-linear fixed-effect regression model to estimate our parameter of curiosity:
$$log(textrm{Items}_{it})= beta log(textrm{Worth})_{it} +gamma_{c(i),t}+ delta_i+ epsilon_{it}$$
$gamma_{c(i),t}$ is a set of category-by-time dummy variables to seize the typical demand in every category-time interval and $delta_i$ is a set of product dummies to seize the time-invariant demand shifter for every product. This “fixed-effect” formulation is customary and customary in lots of regression-based fashions to manage for unobserved confounders. This (pooled) regression mannequin permits us to get better the typical elasticity $beta$ throughout all $N$ items. This may imply that the shop may goal a median worth degree throughout all merchandise of their retailer to maximise the income:
$$underset{textrm{Worth}_t}{max} ;;; textrm{Worth}_{t}cdotmathbb{E}(textrm{Amount}_{t} | textrm{Worth}_{t}, beta)$$
If these items have a pure grouping (product classes), we’d have the ability to establish the typical elasticity of every class by operating separate regressions (or interacting the worth elasticity with the product class) for every class utilizing solely items from that class. This may imply that the shop may goal common costs in every class to maximise category-specific income, such that:
$$underset{textrm{Worth}_{c(i),t}}{max} ;;; textrm{Worth}_{c(i),t}cdotmathbb{E}(textrm{Amount}_{c(i),t} | textrm{Worth}_{c(i),t}, beta_{c(i)})$$
With enough knowledge, we may even run separate regressions for every particular person product to acquire extra granular elasticities.
Nonetheless, real-world knowledge usually presents challenges: some merchandise have minimal worth variation, quick gross sales histories, or class imbalance throughout classes. Beneath these restrictions, operating separate regressions to establish product elasticity would doubtless result in massive customary errors and weak identification of $beta$. HB fashions addresses these points by permitting us to acquire granular estimates of the coefficient of curiosity by sharing statistical power each throughout completely different groupings whereas preserving heterogeneity. With the HB formulation, it’s attainable to run one single regression (just like the pooled case) whereas nonetheless recovering elasticities on the product degree, permitting for granular optimizations.
Understanding Hierarchical Bayesian Fashions
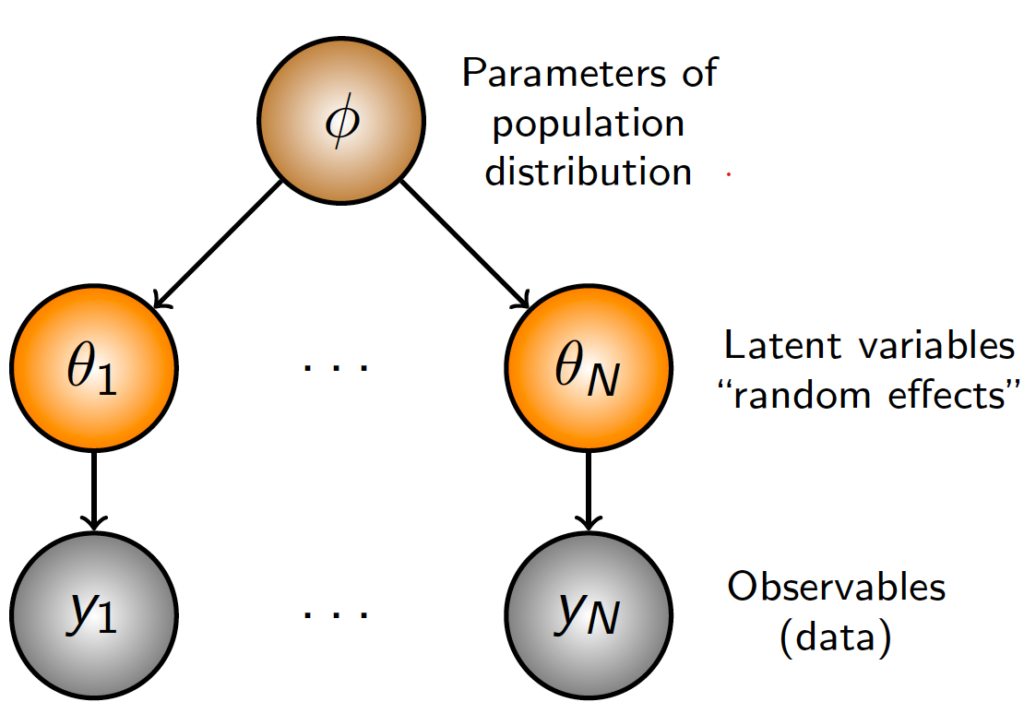
At its core, HB is about recognizing the pure construction in our knowledge. Slightly than treating all observations as fully unbiased (many separate regressions) or forcing them to observe equivalent patterns (one pooled regression), we acknowledge that observations can cluster into teams, with merchandise inside every group sharing comparable patterns. The “hierarchical” side refers to how we manage our parameters in numerous ranges. In its most elementary format, we may have:
- A World parameter that applies to all knowledge.
- Group-level parameters that apply to observations inside that group.
- Particular person-level parameters that apply to every particular particular person.
This technique is versatile sufficient so as to add or take away hierarchies as wanted, relying on the specified degree of pooling. For instance, if we predict there aren’t any similarities throughout classes, we may take away the worldwide parameter. If we predict that these merchandise haven’t any pure groupings, we may take away the group-level parameters. If we solely care concerning the group-level impact, we are able to take away the individual-level parameter and have the group-level coefficients as our most granular parameter. If there exists the presence of subgroups nested throughout the teams, we are able to add one other hierarchical layer. The chances are limitless!
The “Bayesian” side refers to how we replace our beliefs about these parameters based mostly on noticed knowledge. We first begin with a proposed prior distribution that signify our preliminary perception of those parameters, then replace them iteratively to get better a posterior distributions that includes the data from the info. In apply, which means that we use the global-level estimate to tell our group-level estimates, and the group-level parameters to tell the unit-level parameters. Items with a bigger variety of observations are allowed to deviate extra from the group-level means, whereas items with a restricted variety of observations are pulled nearer to the means.
Let’s formalize this with our worth elasticity instance, the place we (ideally) wish to get better the unit-level worth elasticity. We estimate:
$$log(textrm{Items}_{it})= beta_i log(textrm{Worth})_{it} +gamma_{c(i),t} + delta_i + epsilon_{it}$$
The place:
- $beta_i sim textrm{Regular}(beta_{cleft(iright)},sigma_i)$
- $beta_{c(i)}sim textrm{Regular}(beta_g,sigma_{c(i)})$
- $beta_gsim textrm{Regular}(mu,sigma)$
The one distinction from the primary equation is that we substitute the worldwide $beta$ time period with product-level betas $beta_i$. We specify that the unit degree elasticity $beta_i$ is drawn from a standard distribution centered across the category-level elasticity common $beta_{c(i)}$, which is drawn from a shared world elasticity $beta_g$ for all teams. For the unfold of the distribution $sigma$, we are able to assume a hierarchical construction for that too, however on this instance, we simply set fundamental priors for them to take care of simplicity. For this software, we assume a previous perception of: ${ mu= -2, sigma= 1, sigma_{c(i)}=1, sigma_i=1}$. This formulation of the prior assumes that the worldwide elasticity is elastic, 95% of the elasticities fall between -4 and 0, with a regular deviation of 1 at every hierarchical degree. To check whether or not these priors are appropriately specified, we might do a prior predictive checks (not coated on this article) to see whether or not our prior beliefs can get better the info that we observe.
This hierarchical construction permits info to stream between merchandise in the identical class and throughout classes. If a specific product has restricted worth variation knowledge, its elasticity can be pulled towards the class elasticity $beta_{c(i)}$. Equally, classes with fewer merchandise can be influenced extra by the worldwide elasticity, which derives its imply from all class elasticities. The great thing about this strategy is that the diploma of “pooling” occurs routinely based mostly on the info. Merchandise with a number of worth variation will keep estimates nearer to their particular person knowledge patterns, whereas these with sparse knowledge will borrow extra power from their group.
Implementation
On this part, we implement the above mannequin utilizing the Numpyro bundle in Python, a light-weight probabilistic programming language powered by JAX for autograd and JIT compilation to GPU/TPU/CPU. We begin off by producing our artificial knowledge, defining the mannequin, and becoming the mannequin to the info. We shut out with some visualizations of the outcomes.
Information Producing Course of
We simulate gross sales knowledge the place demand follows a log-linear relationship with worth and the product-level elasticity is generated from a Gaussian distribution $beta_i sim textrm{Regular}(-2, 0.7)$. We add in a random worth change each time interval with a $50%$ likelihood, category-specific time developments, and random noise. This provides in multiplicatively to generate our log anticipated demand. From the log anticipated demand, we exponentiate to get the precise demand, and draw realized items offered from a Poisson distribution. We then filter to maintain solely items with greater than 100 items offered (helps accuracy of estimates, not a needed step), and are left with $N=11,798$ merchandise over $T = 156$ intervals (weekly knowledge for 3 years). From this dataset, the true world elasticity is $beta_g = -1.6$, with category-level elasticities starting from $beta_{c(i)} in [-1.68, -1.48]$.
Remember that this DGP ignores loads of real-world intricacies. We don’t mannequin any components that would collectively have an effect on each costs and demand (similar to promotions), and we don’t mannequin any confounders. This instance is solely meant to indicate that we are able to get better the product-specific elasticity underneath a wells-specified mannequin, and doesn’t intention to cowl easy methods to appropriately establish that worth is exogenous. Nonetheless, I counsel that readers confer with Causal Inference for the Brave and True for an introduction to causal inference.
import numpy as np
import pandas as pd
def generate_price_elasticity_data(N: int = 1000,
C: int = 10,
T: int = 50,
price_change_prob: float = 0.2,
seed = 42) -> pd.DataFrame:
"""
Generate artificial knowledge for worth elasticity of demand evaluation.
Information is generated by
"""
if seed shouldn't be None:
np.random.seed(seed)
# Class demand and developments
category_base_demand = np.random.uniform(1000, 10000, C)
category_time_trends = np.random.uniform(0, 0.01, C)
category_volatility = np.random.uniform(0.01, 0.05, C) # Random volatility for every class
category_demand_paths = np.zeros((C, T))
category_demand_paths[:, 0] = 1.0
shocks = np.random.regular(0, 1, (C, T-1)) * category_volatility[:, np.newaxis]
developments = category_time_trends[:, np.newaxis] * np.ones((C, T-1))
cumulative_effects = np.cumsum(developments + shocks, axis=1)
category_demand_paths[:, 1:] = category_demand_paths[:, 0:1] + cumulative_effects
# product results
product_categories = np.random.randint(0, C, N)
product_a = np.random.regular(-2, .7, dimension=N)
product_a = np.clip(product_a, -5, -.1)
# Preliminary costs for every product
initial_prices = np.random.uniform(100, 1000, N)
costs = np.zeros((N, T))
costs[:, 0] = initial_prices
# Generate random values and whether or not costs modified
random_values = np.random.rand(N, T-1)
change_mask = random_values < price_change_prob
# Generate change components (-20% to +20%)
change_factors = 1 + np.random.uniform(-0.2, 0.2, dimension=(N, T-1))
# Create a matrix to carry multipliers
multipliers = np.ones((N, T-1))
# Apply change components solely the place modifications ought to happen
multipliers[change_mask] = change_factors[change_mask]
# Apply the modifications cumulatively to propagate costs
for t in vary(1, T):
costs[:, t] = costs[:, t-1] * multipliers[:, t-1]
# Generate product-specific multipliers
product_multipliers = np.random.lognormal(3, 0.5, dimension=N)
# Get time results for every product's class (form: N x T)
time_effects = category_demand_paths[product_categories][:, np.newaxis, :].squeeze(1)
# Guarantee time results do not go adverse
time_effects = np.most(0.1, time_effects)
# Generate interval noise for all merchandise and time intervals
period_noise = 1 + np.random.uniform(-0.05, 0.05, dimension=(N, T))
# Get class base demand for every product
category_base = category_base_demand[product_categories]
# Calculate base demand
base_demand = (category_base[:, np.newaxis] *
product_multipliers[:, np.newaxis] *
time_effects *
period_noise)
# log demand
alpha_ijt = np.log(base_demand)
# log worth
log_prices = np.log(costs)
# log anticipated demand
log_lambda = alpha_ijt + product_a[:, np.newaxis] * log_prices
# Convert again from log area to get fee parameters
lambda_vals = np.exp(log_lambda)
# Generate items offered
units_sold = np.random.poisson(lambda_vals) # Form: (N, T)
# Create index arrays for all mixtures of merchandise and time intervals
product_indices, time_indices = np.meshgrid(np.arange(N), np.arange(T), indexing='ij')
product_indices = product_indices.flatten()
time_indices = time_indices.flatten()
# Get classes for all merchandise
classes = product_categories[product_indices]
# Get all costs and items offered
all_prices = np.spherical(costs[product_indices, time_indices], 2)
all_units_sold = units_sold[product_indices, time_indices]
# Calculate elasticities
product_elasticity = product_a[product_indices]
df = pd.DataFrame({
'product': product_indices,
'class': classes,
'time_period': time_indices,
'worth': all_prices,
'units_sold': all_units_sold,
'product_elasticity': product_elasticity
})
return df
# Maintain solely items with >X gross sales
def filter_dataframe(df, min_units = 100):
temp = df[['product','units_sold']].groupby('product').sum().reset_index()
unit_filter = temp[temp.units_sold>min_units]['product'].distinctive()
filtered_df = df[df['product'].isin(unit_filter)].copy()
# Abstract
original_product_count = df['product'].nunique()
remaining_product_count = filtered_df['product'].nunique()
filtered_out = original_product_count - remaining_product_count
print(f"Filtering abstract:")
print(f"- Authentic variety of merchandise: {original_product_count}")
print(f"- Merchandise with > {min_units} items: {remaining_product_count}")
print(f"- Merchandise filtered out: {filtered_out} ({filtered_out/original_product_count:.1%})")
# World and class elasticity
global_elasticity = filtered_df['product_elasticity'].imply()
filtered_df['global_elasticity'] = global_elasticity
# Class elasticity
category_elasticities = filtered_df.groupby('class')['product_elasticity'].imply().reset_index()
category_elasticities.columns = ['category', 'category_elasticity']
filtered_df = filtered_df.merge(category_elasticities, on='class', how='left')
# Abstract
print(f"nElasticity Data:")
print(f"- World elasticity: {global_elasticity:.3f}")
print(f"- Class elasticities vary: {category_elasticities['category_elasticity'].min():.3f} to {category_elasticities['category_elasticity'].max():.3f}")
return filtered_df
df = generate_price_elasticity_data(N = 20000, T = 156, price_change_prob=.5, seed=42)
df = filter_dataframe(df)
df.loc[:,'cat_by_time'] = df['category'].astype(str) + '-' + df['time_period'].astype(str)
df.head()
Filtering abstract:
- Authentic variety of merchandise: 20000
- Merchandise with > 100 items: 11798
- Merchandise filtered out: 8202 (41.0%)
Elasticity Data:
- World elasticity: -1.598
- Class elasticities vary: -1.681 to -1.482
| product | class | time_period | worth | units_sold | product_elasticity | category_elasticity | global_elasticity | cat_by_time |
|---|---|---|---|---|---|---|---|---|
| 0 | 8 | 0 | 125.95 | 550 | -1.185907 | -1.63475 | -1.597683 | 8-0 |
| 0 | 8 | 1 | 125.95 | 504 | -1.185907 | -1.63475 | -1.597683 | 8-1 |
| 0 | 8 | 2 | 149.59 | 388 | -1.185907 | -1.63475 | -1.597683 | 8-2 |
| 0 | 8 | 3 | 149.59 | 349 | -1.185907 | -1.63475 | -1.597683 | 8-3 |
| 0 | 8 | 4 | 176.56 | 287 | -1.185907 | -1.63475 | -1.597683 | 8-4 |
Mannequin
We start by creating indices for merchandise, classes, and category-time mixtures utilizing pd.factorize(). This enables us to seelct the right parameter for every commentary. We then convert the worth (logged) and items collection into JAX arrays, then create plates that corresponds to every of our parameter teams. These plates retailer the parameters values for every degree of the hierarchy, together with storing the parameters representing the fastened results.
The mannequin makes use of NumPyro’s plate to outline the parameter teams:
global_a: 1 world worth elasticity parameter with a $textrm{Regular}(-2, 1)$ prior.category_a: $C=10$ category-level elasticities with priors centered on the worldwide parameter and customary deviation of 1.product_a: $N=11,798$ product-specific elasticities with priors centered on their respective class parameters and customary deviation of 1.product_effect: $N=11,798$ product-specific baseline demand results with a regular deviation of three.time_cat_effects: $(T=156)cdot(C=10)$ time-varying results particular to every category-time mixture with a regular deviation of three.
We then reparameterize the parameters utilizing The LocScaleReparam() argument to enhance sampling effectivity and keep away from funneling. After creating the parameters, we calculate log anticipated demand, then convert it again to a fee parameter with clipping for numerical stability. Lastly, we name on the info plate to pattern from a Poisson distribution with the calculated fee parameter. The optimization algorithm will then discover the values of the parameters that greatest match the info utilizing stochastic gradient descent. Under is a graphical illustration of the mannequin to indicate the connection between the parameters.
import jax
import jax.numpy as jnp
import numpyro
import numpyro.distributions as dist
from numpyro.infer.reparam import LocScaleReparam
def mannequin(df: pd.DataFrame, consequence: None):
# Outline indexes
product_idx, unique_product = pd.factorize(df['product'])
cat_idx, unique_category = pd.factorize(df['category'])
time_cat_idx, unique_time_cat = pd.factorize(df['cat_by_time'])
# Convert the worth and items collection to jax arrays
log_price = jnp.log(df.worth.values)
consequence = jnp.array(consequence) if consequence shouldn't be None else None
# Generate mapping
product_to_category = jnp.array(pd.DataFrame({'product': product_idx, 'class': cat_idx}).drop_duplicates().class.values, dtype=np.int16)
# Create the plates to retailer parameters
category_plate = numpyro.plate("class", unique_category.form[0])
time_cat_plate = numpyro.plate("time_cat", unique_time_cat.form[0])
product_plate = numpyro.plate("product", unique_product.form[0])
data_plate = numpyro.plate("knowledge", dimension=consequence.form[0])
# DEFINING MODEL PARAMETERS
global_a = numpyro.pattern("global_a", dist.Regular(-2, 1), infer={"reparam": LocScaleReparam()})
with category_plate:
category_a = numpyro.pattern("category_a", dist.Regular(global_a, 1), infer={"reparam": LocScaleReparam()})
with product_plate:
product_a = numpyro.pattern("product_a", dist.Regular(category_a[product_to_category], 2), infer={"reparam": LocScaleReparam()})
product_effect = numpyro.pattern("product_effect", dist.Regular(0, 3))
with time_cat_plate:
time_cat_effects = numpyro.pattern("time_cat_effects", dist.Regular(0, 3))
# Calculating anticipated demand
def calculate_demand():
log_demand = product_a[product_idx]*log_price + time_cat_effects[time_cat_idx] + product_effect[product_idx]
expected_demand = jnp.exp(jnp.clip(log_demand, -4, 20)) # clip for stability
return expected_demand
demand = calculate_demand()
with data_plate:
numpyro.pattern(
"obs",
dist.Poisson(demand),
obs=consequence
)
numpyro.render_model(
mannequin=mannequin,
model_kwargs={"df": df,"consequence": df['units_sold']},
render_distributions=True,
render_params=True,
)
Estimation
Whereas there are a number of methods to estimate this equation, we use Stochastic Variational Inference (SVI) for this explicit software. As an outline, SVI is a gradient-based optimization technique to reduce the KL-divergence between a proposed posterior distribution to the true posterior distribution by minimizing the ELBO. It is a completely different estimation approach from Markov-Chain Monte Carlo (MCMC), which samples straight from the true posterior distribution. In real-world functions, SVI is extra environment friendly and simply scales to massive datasets. For this software, we set a random seed, initialize the information (household of posterior distribution, assumed to be a Diagonal Regular), outline the training fee schedule and optimizer in Optax, and run the optimization for 1,000,000 (takes ~1 hour) iterations. Whereas the mannequin may need converged beforehand, the loss nonetheless improves by a minor quantity even after operating the optimization for 1,000,000 iterations. Lastly, we plot the (log) losses.

from numpyro.infer import SVI, Trace_ELBO, autoguide, init_to_sample
import optax
import matplotlib.pyplot as plt
rng_key = jax.random.PRNGKey(42)
information = autoguide.AutoNormal(mannequin, init_loc_fn=init_to_sample)
# Outline a studying fee schedule
learning_rate_schedule = optax.exponential_decay(
init_value=0.01,
transition_steps=1000,
decay_rate=0.99,
staircase = False,
end_value = 1e-5,
)
# Outline the optimizer
optimizer = optax.adamw(learning_rate=learning_rate_schedule)
svi = SVI(mannequin, information, optimizer, loss=Trace_ELBO(num_particles=8, vectorize_particles = True))
# Run SVI
svi_result = svi.run(rng_key, 1_000_000, df, df['units_sold'])
plt.semilogy(svi_result.losses);
Recovering Posterior Samples
As soon as the mannequin has been skilled, we are able to can get better the posterior distribution of the parameters by feeding within the ensuing parameters and the preliminary dataset. We can not name the parameters svi_result.params straight since Numpyro makes use of an affline transformation on the back-end for non-Regular distributions. Due to this fact, we pattern 1000 occasions from the posterior distribution and calculate the imply and customary deviation of every parameter in our mannequin. The ultimate a part of the next code creates a dataframe with the estimated elasticity for every product at every hierarchical degree, which we then be a part of again to our unique dataframe to check whether or not the algorithm recovers the true elasticity.
predictive = numpyro.infer.Predictive(
autoguide.AutoNormal(mannequin, init_loc_fn=init_to_sample),
params=svi_result.params,
num_samples=1000
)
samples = predictive(rng_key, df, df['units_sold'])
# Extract means and std dev
outcomes = {}
excluded_keys = ['product_effect', 'time_cat_effects']
for ok, v in samples.objects():
if ok not in excluded_keys:
outcomes[f"{k}"] = np.imply(v, axis=0)
outcomes[f"{k}_std"] = np.std(v, axis=0)
# product elasticity estimates
prod_elasticity_df = pd.DataFrame({
'product': df['product'].distinctive(),
'product_elasticity_svi': outcomes['product_a'],
'product_elasticity_svi_std': outcomes['product_a_std'],
})
result_df = df.merge(prod_elasticity_df, on='product', how='left')
# Class elasticity estimates
prod_elasticity_df = pd.DataFrame({
'class': df['category'].distinctive(),
'category_elasticity_svi': outcomes['category_a'],
'category_elasticity_svi_std': outcomes['category_a_std'],
})
result_df = result_df.merge(prod_elasticity_df, on='class', how='left')
# World elasticity estimates
result_df['global_a_svi'] = outcomes['global_a']
result_df['global_a_svi_std'] = outcomes['global_a_std']
result_df.head()
| product | class | time_period | worth | units_sold | product_elasticity | category_elasticity | global_elasticity | cat_by_time | product_elasticity_svi | product_elasticity_svi_std | category_elasticity_svi | category_elasticity_svi_std | global_a_svi | global_a_svi_std |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 8 | 0 | 125.95 | 550 | -1.185907 | -1.63475 | -1.597683 | 8-0 | -1.180956 | 0.000809 | -1.559872 | 0.027621 | -1.5550271 | 0.2952548 |
| 0 | 8 | 1 | 125.95 | 504 | -1.185907 | -1.63475 | -1.597683 | 8-1 | -1.180956 | 0.000809 | -1.559872 | 0.027621 | -1.5550271 | 0.2952548 |
| 0 | 8 | 2 | 149.59 | 388 | -1.185907 | -1.63475 | -1.597683 | 8-2 | -1.180956 | 0.000809 | -1.559872 | 0.027621 | -1.5550271 | 0.2952548 |
| 0 | 8 | 3 | 149.59 | 349 | -1.185907 | -1.63475 | -1.597683 | 8-3 | -1.180956 | 0.000809 | -1.559872 | 0.027621 | -1.5550271 | 0.2952548 |
| 0 | 8 | 4 | 176.56 | 287 | -1.185907 | -1.63475 | -1.597683 | 8-4 | -1.180956 | 0.000809 | -1.559872 | 0.027621 | -1.5550271 | 0.2952548 |
Outcomes
The next code plots the true and estimated elasticities for every product. Every level is ranked by their true elasticity worth (black), and the estimated elasticity from the mannequin can also be proven. We are able to see that the estimated elasticities follows the trail of the true elasticities, with a Imply Absolute Error of round 0.0724. Factors in purple represents merchandise whose 95% CI doesn’t comprise the true elasticity, whereas factors in blue signify merchandise whose 95% CI accommodates the true elasticity. Provided that the worldwide imply is -1.598, this represents a median error of 4.5% on the product degree. We are able to see that the SVI estimates intently observe the sample of the true elasticities however with some noise, significantly because the elasticities turn into increasingly adverse. On the highest proper panel, we plot the connection between the error of the estimated elasticities and the true elasticity values. As true elasticities turn into increasingly adverse, our mannequin turns into much less correct.
For the category-level and global-level elasticities, we are able to create the posteriors utilizing two strategies. We are able to both boostrap all product-level elasticities throughout the class, or we are able to get the category-level estimates straight from the posterior parameters. After we take a look at the category-level elasticity estimates on the underside left, we are able to see that the each the category-level estimates recovered from the mannequin and the bootstrapped samples from the product-level elasticities are additionally barely biased in direction of zero, with an MAE of ~.033. Nonetheless, the arrogance interval given by the category-level parameter covers the true parameter, not like the bootstrapped product-level estimates. This implies that when figuring out group-level elasticities, we should always straight use the group-level parameters as an alternative of bootstrapping the extra granular estimates. When trying on the world degree, each strategies accommodates the true parameter estimate within the 95% confidence bounds, with the worldwide parameter out-performing the product-level bootstrapping, at the price of having bigger customary errors.
Issues
- HB underestimates posterior variance: One disadvantage of utilizing SVI for the estimation is that it underestimates the posterior variance. Whereas we’ll cowl this matter intimately in a later article, the target operate for SVI solely takes into consideration the distinction in expectation of our posited distribution and the true distribution. Which means it doesn’t contemplate the total correlation construction between parameters within the posterior. The mean-field approximation generally utilized in SVI assumes conditional (on the earlier hierarchy’s draw) independence between parameters, which ignores any covariances between merchandise throughout the identical hierarchy. Which means if are any spillover results (similar to cannibalization or cross-price elasticity), it might not be accounted for within the confidence bounds. Because of this mean-field assumption, the uncertainty estimates are usually overly assured, leading to confidence intervals which can be too slim and fail to correctly seize the true parameter values on the anticipated fee. We are able to see within the high left determine that solely 9.7% of the product-level elasticities cowl their true elasticity. In a later put up, we’ll embrace some solutions to this downside.
- Significance of priors: When utilizing HB, priors matter considerably extra in comparison with customary Bayesian approaches. Whereas massive datasets usually permit the chance to dominate priors when estimating world parameters, hierarchical buildings modifications this dynamic and scale back the efficient pattern sizes at every degree. In our mannequin, the worldwide parameter solely sees 10 category-level observations (not the total dataset), classes solely draw from their contained merchandise, and merchandise rely solely on their very own observations. This lowered efficient pattern dimension causes shrinkage, the place outlier estimates (like very adverse elasticities) get pulled towards their class means. This highlights the significance of prior predictive checks, since misspecified priors can have outsized affect on the outcomes.

def elasticity_plots(result_df, outcomes=None):
# Create the determine with 2x2 grid
fig = plt.determine(figsize=(12, 10))
gs = fig.add_gridspec(2, 2)
# product elasticity
ax1 = fig.add_subplot(gs[0, 0])
# Information prep
df_product = result_df[['product','product_elasticity','product_elasticity_svi','product_elasticity_svi_std']].drop_duplicates()
df_product['product_elasticity_svi_lb'] = df_product['product_elasticity_svi'] - 1.96*df_product['product_elasticity_svi_std']
df_product['product_elasticity_svi_ub'] = df_product['product_elasticity_svi'] + 1.96*df_product['product_elasticity_svi_std']
df_product = df_product.sort_values('product_elasticity')
mae_product = np.imply(np.abs(df_product.product_elasticity-df_product.product_elasticity_svi))
colours = []
for i, row in df_product.iterrows():
if (row['product_elasticity'] >= row['product_elasticity_svi_lb'] and
row['product_elasticity'] <= row['product_elasticity_svi_ub']):
colours.append('blue') # Inside CI bounds
else:
colours.append('purple') # Outdoors CI bounds
# Proportion of factors inside bounds
within_bounds_pct = colours.depend('blue') / len(colours) * 100
# Plot knowledge
ax1.scatter(vary(len(df_product)), df_product['product_elasticity'],
shade='black', label='True Elasticity', s=20, zorder=3)
ax1.scatter(vary(len(df_product)), df_product['product_elasticity_svi'],
shade=colours, label=f'SVI Estimate (MAE: {mae_product:.4f}, Protection: {within_bounds_pct:.1f}%)',
s=3, zorder=2)
ax1.set_xlabel('Product Index (sorted by true elasticity)')
ax1.set_ylabel('Elasticity Worth')
ax1.set_title('SVI Estimates of True Product Elasticities')
ax1.legend()
ax1.grid(alpha=0.3)
# Relationship between MAE and true elasticity
ax2 = fig.add_subplot(gs[0, 1])
# Calculate MAE for every product
temp = result_df[['product','product_elasticity', 'product_elasticity_svi']].drop_duplicates().copy()
temp['product_error'] = temp['product_elasticity'] - temp['product_elasticity_svi']
temp['product_mae'] = np.abs(temp['product_error'])
correlation = temp[['product_mae', 'product_elasticity']].corr()
# Plot knowledge
ax2.scatter(temp['product_elasticity'], temp['product_error'], alpha=0.5, s=5, shade = colours)
ax2.set_xlabel('True Elasticity')
ax2.set_ylabel('Error (True - Estimated)')
ax2.set_title('Relationship Between True Elasticity and Estimation Accuracy')
ax2.grid(alpha=0.3)
ax2.textual content(0.5, 0.95, f"Correlation: {correlation.iloc[0,1]:.3f}",
remodel=ax2.transAxes, ha='heart', va='high',
bbox=dict(boxstyle='spherical', facecolor='white', alpha=0.7))
# Class Elasticity
ax3 = fig.add_subplot(gs[1, 0])
# Distinctive classes and elasticities
category_data = result_df[['category', 'category_elasticity', 'category_elasticity_svi', 'category_elasticity_svi_std']].drop_duplicates()
category_data = category_data.sort_values('category_elasticity')
# Bootstrapped means from product elasticities inside every class
bootstrap_means = []
bootstrap_ci_lower = []
bootstrap_ci_upper = []
for cat in category_data['category']:
# Get product elasticities for this class
prod_elasticities = result_df[result_df['category'] == cat]['product_elasticity_svi'].distinctive()
# Bootstrap means
boot_means = [np.mean(np.random.choice(prod_elasticities, size=len(prod_elasticities), replace=True))
for _ in range(1000)]
bootstrap_means.append(np.imply(boot_means))
bootstrap_ci_lower.append(np.percentile(boot_means, 2.5))
bootstrap_ci_upper.append(np.percentile(boot_means, 97.5))
category_data['bootstrap_mean'] = bootstrap_means
category_data['bootstrap_ci_lower'] = bootstrap_ci_lower
category_data['bootstrap_ci_upper'] = bootstrap_ci_upper
# Calculate MAE
mae_category_svi = np.imply(np.abs(category_data['category_elasticity_svi'] - category_data['category_elasticity']))
mae_bootstrap = np.imply(np.abs(category_data['bootstrap_mean'] - category_data['category_elasticity']))
# Plot the info
left_offset = -0.2
right_offset = 0.2
x_range = vary(len(category_data))
ax3.scatter(x_range, category_data['category_elasticity'],
shade='black', label='True Elasticity', s=50, zorder=3)
# Bootstrapped product elasticity
ax3.scatter([x + left_offset for x in x_range], category_data['bootstrap_mean'],
shade='inexperienced', label=f'Bootstrapped Product Estimate (MAE: {mae_bootstrap:.4f})', s=30, zorder=2)
for i in x_range:
ax3.plot([i + left_offset, i + left_offset],
[category_data['bootstrap_ci_lower'].iloc[i], category_data['bootstrap_ci_upper'].iloc[i]],
shade='inexperienced', alpha=0.3, zorder=1)
# category-level SVI estimates
ax3.scatter([x + right_offset for x in x_range], category_data['category_elasticity_svi'],
shade='blue', label=f'Class SVI Estimate (MAE: {mae_category_svi:.4f})', s=30, zorder=2)
for i in x_range:
ci_lower = category_data['category_elasticity_svi'].iloc[i] - 1.96 * category_data['category_elasticity_svi_std'].iloc[i]
ci_upper = category_data['category_elasticity_svi'].iloc[i] + 1.96 * category_data['category_elasticity_svi_std'].iloc[i]
ax3.plot([i + right_offset, i + right_offset], [ci_lower, ci_upper], shade='blue', alpha=0.3, zorder=1)
ax3.set_xlabel('Class Index (sorted by true elasticity)')
ax3.set_ylabel('Elasticity')
ax3.set_title('Comparability with True Class Elasticity')
ax3.legend()
ax3.grid(alpha=0.3)
# world elasticity
ax4 = fig.add_subplot(gs[1, 1])
temp = result_df[['product','product_elasticity_svi','global_elasticity']].drop_duplicates()
bootstrap_means = [np.mean(np.random.choice(np.array(temp['product_elasticity_svi']), 100)) for i in vary(10000)]
global_means = np.random.regular(result_df['global_a_svi'].iloc[0], result_df['global_a_svi_std'].iloc[0], 10000)
true_global = np.distinctive(temp.global_elasticity)[0]
p_mae = np.abs(np.imply(bootstrap_means) - true_global)
g_mae = np.abs(np.imply(global_means) - true_global)
# Plot knowledge
ax4.hist(bootstrap_means, bins=100, alpha=0.3, density=True,
label=f'Product Elasticity Bootstrap (MAE: {p_mae:.4f})')
ax4.hist(global_means, bins=100, alpha=0.3, density=True,
label=f'World Elasticity Distribution (MAE: {g_mae:.4f})')
ax4.axvline(x=true_global, shade='black', linestyle='--', linewidth=2,
label=f'World Elasticity: {true_global:.3f}', zorder=0)
ax4.set_xlabel('Elasticity')
ax4.set_ylabel('Frequency')
ax4.set_title('World Elasticity Comparability')
ax4.legend()
ax4.grid(True, linestyle='--', alpha=0.7)
# Present
plt.tight_layout()
plt.present()
elasticity_plots(result_df)
Conclusion
Alternate Makes use of: Other than estimating worth elasticity of demand, HB fashions even have quite a lot of different makes use of in Data Science. In retail, HB fashions can forecast demand for current shops and remedy the cold-start downside for brand spanking new shops by borrowing info from shops/networks which have already been established and are clustered throughout the identical hierarchy. For advice programs, HB can estimate user-level preferences from a mix of person and item-level traits. This construction allows related suggestions to new customers based mostly on cohort behaviors, progressively transitioning to individualized suggestions as person historical past accumulates. If no cohort groupings are simply accessible, Okay-means can be utilized to group comparable items based mostly on their traits.
Lastly, these fashions may also be used to mix outcomes from experimental and observational research. Scientists can use historic observational uplift estimates (adverts uplift) and complement it with newly developed A/B assessments to cut back the required pattern dimension for experiments by incorporating prior data. This strategy creates a steady studying framework the place every new experiment builds upon earlier findings fairly than ranging from scratch. For groups dealing with useful resource constraints, this implies quicker time-to-insight (particularly when mixed with surrogate models) and extra environment friendly experimentation pipelines.
Ultimate Remarks: Whereas this introduction has highlighted a number of functions of hierarchical Bayesian fashions, we’ve solely scratched the floor. We haven’t deep dived into granular implementation points similar to prior and posterior predictive checks, formal goodness-of-fit assessments, computational scaling, distributed coaching, efficiency of estimation methods (MCMC vs. SVI), and non-nested hierarchical buildings, every of which deserves their very own put up.
However, this overview ought to present a sensible start line for incorporating hierarchical Bayesian into your toolkit. These fashions supply a framework for dealing with (normally) messy, multi-level knowledge buildings which can be usually seen in real-world enterprise issues. As you start implementing these approaches, I’d love to listen to about your experiences, challenges, successes, and new use instances for this class of mannequin, so please attain out with questions, insights, or examples by means of my email or LinkedIn. When you’ve got any suggestions on this text, or wish to request one other matter in causal inference/machine studying, please additionally be happy to achieve out. Thanks for studying!
Note: All photos used on this article is generated by the creator.