Ever surprise how your machine studying fashions work out if two items of information are “comparable” or “far aside”? It’s a basic query, and the reply lies in one thing known as distance metrics. Whether or not you’re classifying information with Okay-Nearest Neighbors (KNN), grouping comparable objects with Okay-Means clustering, or simplifying complicated datasets with dimensionality discount, the way in which you measure this “distance” can dramatically affect how properly your mannequin performs.
In the present day, we’re diving into two of the preferred and influential distance metrics: Euclidean Distance (L2 Norm) and Manhattan Distance (L1 Norm). Your selection between these two can profoundly affect the end result of your machine studying endeavors. We’ll discover what they’re, how they differ, and most significantly, when to make use of every, together with their fascinating connections to regularization methods like Lasso and Ridge Regression.
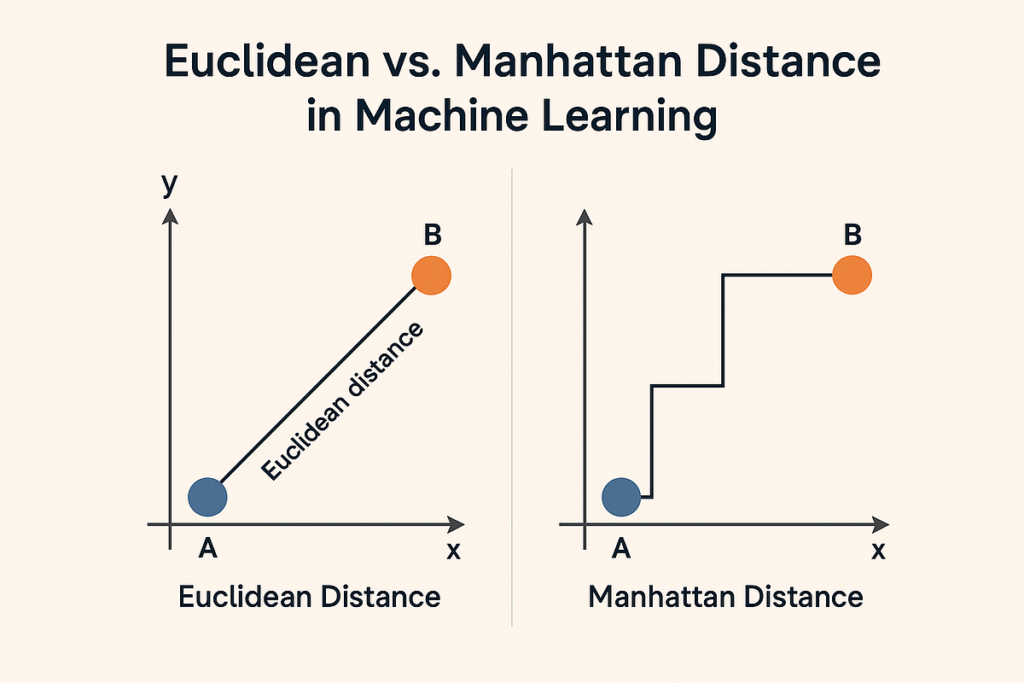
Think about you’re standing at level A and need to get to level B, and there are not any obstacles in your means. You’d naturally take the straightest path potential, proper? That’s precisely what Euclidean distance is. It’s the “because the crow flies” or straight-line distance between two factors in area. Consider it as utilizing a ruler to measure straight from one information level to a different. It’s probably the most intuitive means we usually take into consideration distance in the true world.
Euclidean Distance System:
For 2 factors, P1=(x1,y1) and P2=(x2,y2) in a 2D airplane, the Euclidean distance is:
This may be prolonged to greater dimensions.
When to Use Euclidean Distance:
- When your options are steady and usually distributed: Euclidean distance works finest when your information flows easily and symmetrically round its common.
- When relationships between options are linear: If adjustments in a single characteristic correspond proportionally to adjustments in one other, Euclidean distance usually captures that relationship properly.
- When exact geometric proximity is required: If the precise bodily distance or direct spatial relationship between information factors is significant to your downside.
Algorithms That Generally Use L2 Distance:
- Okay-Means Clustering: This algorithm teams information factors based mostly on their proximity to cluster facilities, usually outlined by Euclidean distance.
- Principal Element Evaluation (PCA): This dimensionality discount method goals to protect the variance, which is usually interpreted by way of Euclidean distances.
- Help Vector Machines (SVMs): Whereas indirectly a distance metric in its core, the idea of a margin (distance to a hyperplane) in SVMs usually pertains to Euclidean distance.
- Linear Regression: The usual least squares goal operate minimizes the sum of squared errors, which is straight associated to Euclidean distance between predicted and precise values.
Now, think about you’re a taxi driver in a metropolis with an ideal grid of streets, like Manhattan. To get from one block to a different, you’ll be able to’t lower diagonally by way of buildings. It’s important to drive alongside the streets, turning solely at intersections. This “comply with the grid” method is strictly what Manhattan distance, also referred to as Taxicab or Metropolis Block distance, represents. It’s the sum of absolutely the variations between the coordinates of two factors.
Manhattan Distance System:
For 2 factors, P1=(x1,y1) and P2=(x2,y2) in a 2D airplane, the Manhattan distance is:
This can be prolonged to greater dimensions.
When to Use Manhattan Distance:
- When information is sparse or high-dimensional: In datasets with many options, particularly the place many values are zero (sparse information), Manhattan distance may be more practical because it’s much less delicate to the “curse of dimensionality.”
- When options are usually not correlated: If every characteristic contributes independently to the general distance, Manhattan distance treats every dimension equally with out squaring variations.
- While you need robustness to outliers: As a result of it makes use of absolute variations as an alternative of squared variations, Manhattan distance is much less affected by excessive values (outliers) in your information. A single giant distinction received’t disproportionately skew the full distance.
Algorithms That Can Use L1 Distance:
- KNN (instead metric): Whereas Euclidean is frequent, KNN can definitely use Manhattan distance, particularly when the circumstances talked about above apply.
- Okay-Medians Clustering: Much like Okay-Means, however makes use of medians as an alternative of means, which makes it extra strong to outliers and sometimes pairs properly with L1 distance.
- Optimization issues with axis-aligned constraints: In situations the place motion is restricted alongside particular axes, or prices are linearly additive throughout dimensions.
- Compressed Sensing and Sparse Restoration: Many algorithms in these fields leverage the L1 norm to advertise sparsity in options.
The ideas of L1 and L2 aren’t only for measuring distances between information factors; they’re additionally tremendous essential in regularization for regression fashions, influencing how your mannequin learns from information.
In machine studying, we generally encounter points like overfitting. That is when a mannequin learns the coaching information too properly, capturing noise and particular patterns that don’t generalize to new, unseen information. Regularization is a method used to forestall overfitting by including a penalty time period to the loss operate throughout mannequin coaching. This penalty discourages the mannequin from assigning excessively giant weights to options, thereby making the mannequin less complicated and extra strong.
L1 Regularization (Lasso): This methodology makes use of the Manhattan (L1) norm to penalize giant weights assigned to options. What’s neat about Lasso is that it encourages sparsity, that means it could truly drive some characteristic weights precisely to zero. This makes it improbable for characteristic choice as a result of it successfully tells you which ones options are most essential by eliminating the much less related ones. It’s like having a built-in characteristic significance detector.
L2 Regularization (Ridge): On the flip aspect, Ridge regularization employs the Euclidean (L2) norm to penalize weights. As a substitute of slicing options out totally, Ridge regularization shrinks all weights easily with out eliminating any of them. That is significantly helpful for those who’re coping with multicollinearity (when your options are extremely correlated) and need to hold all of your options within the mannequin, even when some have much less affect. It helps in distributing the affect of correlated options extra evenly.
So, choosing between L1 and L2 isn’t nearly the way you measure distance in a dataset; it basically shapes your total modeling technique, impacting all the pieces from characteristic choice to dealing with multicollinearity.
In the end, distance metrics are way more than simply mathematical formulation. They’re a mirrored image of the way you need your mannequin to behave and what sort of insights you need to achieve out of your information. Whether or not you go for Euclidean (L2) to measure direct proximity or Manhattan (L1) to account for grid-like actions or outlier robustness, your determination impacts all the pieces from how simply you’ll be able to interpret your mannequin to its general efficiency. Selecting correctly is a key step in constructing efficient machine studying options.