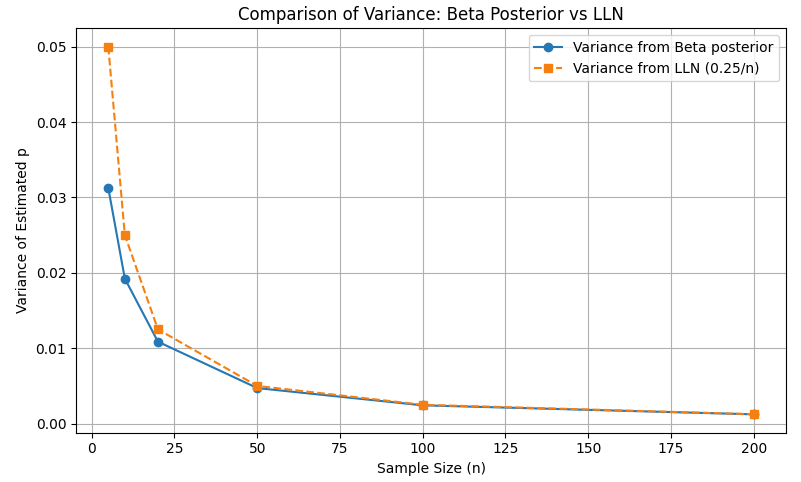
To exhibit this, right here’s a Python script that compares Beta-derived variance with the classical LLN formulation:
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import beta# Pattern sizes and corresponding Beta parameters assuming 50% success price
sample_sizes = [5, 10, 20, 50, 100, 200]
variances = []
# Assume uniform prior: Beta(1, 1) → posterior Beta(x + 1, n - x + 1)
# For 50% success price: x = n / 2 ⇒ α = n/2 + 1, β = n/2 + 1
for n in sample_sizes:
alpha = n / 2 + 1
beta_param = n / 2 + 1
var = (alpha * beta_param) / ((alpha + beta_param) ** 2 * (alpha + beta_param + 1))
variances.append(var)
# LLN theoretical variance of pattern imply for Bernoulli(0.5): Var = p(1-p)/n = 0.25/n
lln_variances = [0.25 / n for n in sample_sizes]
# Plot the variance from Beta and LLN facet by facet
plt.determine(figsize=(8, 5))
plt.plot(sample_sizes, variances, 'o-', label="Variance from Beta posterior")
plt.plot(sample_sizes, lln_variances, 's--', label="Variance from LLN (0.25/n)")
plt.xlabel("Pattern Measurement (n)")
plt.ylabel("Variance of Estimated p")
plt.title("Comparability of Variance: Beta Posterior vs LLN")
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.present()
As proven, the Beta-derived variance intently tracks the LLN prediction however gives a extra conservative estimate for small n, which visually corresponds to a “fatter” uncertainty curve.