Graph principle is a cornerstone of discrete arithmetic and pc science, offering instruments for modeling and analyzing advanced relationships. Graphs, collections of vertices linked by edges, are used to signify a various vary of methods in fields akin to pc networks, transportation, biology, and social networks. Understanding the interactions inside these methods can reveal insights into all the pieces from the unfold of ailments to the optimum routes for supply vans.
In graph principle, the problem lies not solely in fixing particular person issues but additionally in making use of applicable algorithms to deal with the complexities of real-world graphs. Whereas classical algorithms have served as highly effective instruments, they’re usually constrained by scalability and limitations of predefined heuristics. With the rise of machine studying, significantly Graph Neural Networks (GNNs), new potentialities have emerged for fixing graph-related issues. By extending the capabilities of classical algorithms, GNNs promise to supply options that scale higher and generalize extra successfully throughout various graph constructions.
Graph Sorts and Terminology
The core components of any graph are the entities it represents and the relationships between them. Understanding how these parts join then permits for evaluation of patterns and relationships inside a graph.
- Vertices (Nodes): These are the entities in a graph.
- Edges: These signify the relationships between the nodes.
- Paths: A path is a sequence of edges that connects a sequence of nodes.
Graphs may be distinguished by their relationships, what data their edges could carry, and different distinctive constructions that might be helpful in evaluation and functions.
- Directed vs. Undirected Graphs: In a directed graph, edges have route, which means an edge from one vertex to a different doesn’t indicate the reverse. In an undirected graph, the sides are bidirectional.
- Weighted vs. Unweighted Graphs: A weighted graph assigns a weight to every edge, often representing some attribute like distance or value. In an unweighted graph, edges are binary, solely indicating the existence of a connection.
- Bipartite Graphs: A bipartite graph is a particular sort of graph the place the set of vertices may be divided into two disjoint units, and each edge connects a vertex in a single set to a vertex within the different. Bipartite graphs are vital in functions like matching issues and suggestion methods.
Classical Graph Principle Issues
Graph principle underpins many issues in pc science, and several other basic issues are vital for fields akin to community evaluation, transportation, biology, and social sciences. These issues usually depend on environment friendly algorithms and heuristic strategies to supply options.
Shortest Path Downside
The shortest path downside entails discovering the shortest path between two nodes in a graph, the place paths could have completely different lengths. It may be solved utilizing Dijkstra’s Algorithm (for non-negative weights) or Bellman-Ford (for graphs with detrimental weights). This downside is prime in community routing and logistics.
Touring Salesman Downside
The Touring Salesman Downside (TSP) is an NP-hard optimization downside the place the target is to search out the shortest potential route that visits every node precisely as soon as and returns to the origin node. Actual options are sometimes impractical for giant graphs, and heuristics are sometimes used as a substitute due to this.
Graph Coloring
The graph coloring downside entails assigning colours to vertices such that no two adjoining vertices share the identical shade. This downside has functions in scheduling, useful resource allocation, and register allocation in compilers.
Neighborhood Detection
Neighborhood detection goals to establish teams of nodes (communities) which might be extra densely linked internally than with the remainder of the graph. This downside is prime in analyzing social networks for social media platforms, the place communities signify tightly-knit teams of people.
Limitations of Classical Algorithms
Whereas conventional algorithms like Dijkstra’s for shortest paths or dynamic programming for TSP are extremely efficient, they usually encounter points when it comes to:
- Scalability: These algorithms battle with very giant graphs. For instance, Dijkstra’s algorithm has a time complexity of O(V²), which turns into inefficient because the graph measurement will increase.
- Combinatorial Explosion: Issues like TSP are NP-hard, which means the time complexity grows exponentially as the dimensions of the graph will increase, making them infeasible for large-scale situations.
- Mounted Heuristics: Many classical algorithms depend on predefined heuristics that won’t generalize effectively throughout completely different issues.
Graph Neural Networks are a category of deep studying fashions that generalize neural networks to graph-structured knowledge. By doing so, they supply a approach to study node and edge embeddings by performing message-passing and aggregation operations throughout the graph. The purpose of a GNN is to study a illustration, or embedding, for every node within the graph, which captures each the native and world graph constructions.
The core of a GNN entails a message-passing framework, the place nodes alternate data with their neighbors to replace their representations iteratively. This permits GNNs to generalize effectively throughout various kinds of graph knowledge with out requiring specific characteristic engineering.
The message-passing framework is usually composed of two key steps:
- Aggregation: On this step, a node aggregates messages (data) from its neighbors. This may be carried out utilizing easy features akin to summation, averaging, or taking the utmost of its neighbors’ options.
- Replace: After aggregating the knowledge, the node updates its personal illustration primarily based on the aggregated message. This step is usually applied utilizing a feed-forward neural community.
Why GNNs Are Efficient for Graph Issues
Graph neural networks supply a number of benefits over conventional graph algorithms. GNNs enable for end-to-end studying, the place each characteristic extraction and prediction are realized from the information itself. With this, the necessity for hand-crafted heuristics or predefined guidelines is eradicated. GNNs may also be made extra scalable than conventional strategies for giant graphs utilizing strategies akin to graph sampling, mini-batch processing, and graph convolution strategies. They’re additionally extra versatile and may deal with numerous forms of graph-related duties akin to node classification, graph classification, hyperlink prediction, and even optimization issues. Lastly, not like conventional algorithms that course of one node or edge at a time, GNNs may be extremely parallelized, making them extra appropriate for large-scale functions.
Forms of GNN Architectures
There are a number of key GNN architectures fitted to numerous completely different duties. Graph Convolutional Networks (GCNs) prolong the concept of convolutional neural networks to knowledge structured as graphs by performing localized aggregation of node options. Every layer performs a convolution operation over the graph to replace the node representations. Graph Pattern and Aggregation (GraphSAGE), as a substitute of utilizing all neighbors for aggregation as in GCNs, samples a fixed-size set of neighbors for every node. This permits it to scale higher to bigger graphs. Graph Consideration Networks (GATs) introduce consideration mechanisms into GNNs so nodes can weigh their neighbors’ contributions through the aggregation course of. That is helpful when the graph construction will not be uniform or when some neighbors may be extra necessary than others.
Shortest Path Downside
The shortest path downside may be modeled as a graph traversal process. Whereas conventional algorithms are nonetheless extremely environment friendly, GNNs present a data-driven method to study patterns within the graph and generalize throughout numerous varieties as effectively. A GNN may be educated to foretell the shortest path from a supply node to different nodes by incorporating the graph construction within the mannequin. The important thing problem right here is to design the loss operate so the GNN learns to approximate the shortest path lengths.
Coaching Process:
- Graph Era: The graph may be represented utilizing an adjacency matrix, the place nodes have options primarily based on their distances from the supply node.
- Mannequin Structure: A GCN can be utilized to study the node embeddings. The output node embeddings are then in comparison with the true shortest path lengths, doubtlessly by utilizing a Imply Squared Error (MSE) loss.
- Optimization: The mannequin may be educated utilizing the Stochastic Gradient Descent (SGD) or Adam optimization algorithms.
Touring Salesman Downside
TSP has an answer area that grows exponentially with the variety of nodes. Conventional approaches like dynamic programming or branch-and-bound are computationally costly, so by utilizing GNNs, the optimum resolution may be approximated extra effectively. A GNN can be utilized to foretell the subsequent node within the optimum path primarily based on the present state of the answer and the present node. That is usually carried out by treating the issue as reinforcement studying, the place the GNN learns tips on how to navigate the graph to attenuate the associated fee.
Coaching Process:
- Graph Era: The graph used is usually a weighted full graph, the place edges signify pairwise prices between all nodes.
- Mannequin Structure: A GCN or attention-based GNN can be utilized to take the graph construction and node/edge options as enter. The GNN could output possibilities (like a warmth map) that every edge is within the optimum path, and a surrogate/unsupervised loss could also be used.
- Optimization: The mannequin may be educated utilizing gradient-based optimizers akin to SGD or Adam.
With this preliminary information, a sensible implementation of GNNs may be explored, with the target of predicting the shortest path lengths from a particular supply node to each different node within the graph utilizing GCN layers.
Imports and Setup
First, the mandatory libraries are imported. These will likely be helpful for a lot of duties, together with coaching the neural community, dealing with graph-based knowledge, visualization, and extra
import torch
import torch.nn.useful as F
from torch_geometric.nn import GCNConv
from torch_geometric.knowledge import Information
import networkx as nx
import matplotlib.pyplot as plt
import numpy as np
from sklearn.model_selection import train_test_splittorch.manual_seed(42)
np.random.seed(42)
Generate a Random Graph
To create an unbiased instance for this mission’s goal, random undirected graphs may be generated utilizing the Erdos-Renyi mannequin with a specified variety of nodes and edge chance. On this case, 20 nodes are generated with an edge chance of 0.3. That is basically a easy random graph mannequin and is mostly helpful for testing algorithms on graphs with various connectivity. On this operate, the sides are additionally weighted with random values between 1 and 10. These weights will likely be used to affect the graph convolution operations within the neural community.
def generate_graph(num_nodes=20, edge_prob=0.3):
G = nx.erdos_renyi_graph(num_nodes, edge_prob)
for (u, v) in G.edges():
G.edges[u, v]['weight'] = np.random.uniform(1, 10)
return G
Convert the Graph to PyTorch Geometric Information
This operate converts the generated graph right into a format appropriate for PyTorch Geometric and returns the information required for truly coaching the GCN. In GCNs, edges are represented by an edge_index tensor, which is a 2xE matrix the place E is the variety of edges. Every column represents a directed edge from one node to a different, and the code provides each instructions for every edge for the reason that graph is undirected. Node options are additionally primarily based on the node diploma (variety of neighbors), which is an easy scalar characteristic used within the GCN mannequin. The labels signify the shortest path lengths from a specified supply node to all different nodes, and these values are calculated initially utilizing Dijkstra’s algorithm. The operate then returns a Information object that holds all the mandatory data to coach the GCN, together with node options, graph construction, edge weights, and floor fact labels.
def graph_to_data(G, source_node=0):
edge_index = []
edge_attr = []for u, v, knowledge in G.edges(knowledge=True):
edge_index += [[u, v], [v, u]]
edge_attr += [[data['weight']]] * 2
edge_index = torch.tensor(edge_index, dtype=torch.lengthy).t().contiguous()
edge_attr = torch.tensor(edge_attr, dtype=torch.float)
x = torch.tensor([[G.degree[i]] for i in vary(G.number_of_nodes())], dtype=torch.float)
sp_lengths = nx.single_source_dijkstra_path_length(G, supply=source_node)
y = torch.tensor([sp_lengths.get(i, float('inf')) for i in range(G.number_of_nodes())], dtype=torch.float)
return Information(x=x, edge_index=edge_index, edge_attr=edge_attr, y=y), G
GCN Mannequin
The GCN mannequin is outlined right here utilizing two GCNConv layers, or graph convolution layers from PyTorch Geometric. It computes the brand new node options by aggregating data from neighbors, weighted by the sides. The primary layer transforms the node options, and the second transforms the options additional, outputting a scalar worth for every node for prediction. Right here, 1-dimensional values are outputted since it’s the shortest path size that’s being predicted.
After the primary GCN layer, the output is handed via a RELU activation operate, which introduces non-linearity, serving to the community study advanced relationships between nodes. As well as, the ahead methodology takes in a Information object containing the graph’s node options and edge indices, applies the graph convolutions, and eventually returns the anticipated node labels.
class GCN(torch.nn.Module):
def __init__(self, input_dim, hidden_dim):
tremendous(GCN, self).__init__()
self.conv1 = GCNConv(input_dim, hidden_dim)
self.conv2 = GCNConv(hidden_dim, 1)def ahead(self, knowledge):
x, edge_index = knowledge.x, knowledge.edge_index
x = F.relu(self.conv1(x, edge_index))
x = self.conv2(x, edge_index)
return x.squeeze()
Coaching the Mannequin
This operate handles the coaching loop of the GCN mannequin. It’s initialized with an enter dimension akin to the variety of node options and a hidden dimension of 32. The Adam optimizer is used to replace the mannequin’s parameters throughout coaching, and is fashionable in machine studying due to its adaptive studying charge and momentum capabilities, serving to quicker convergence. The loss operate used is MSE loss, which measures the squared distinction between predicted and true values.
As for the coaching loop, for every epoch, the mannequin is ready to coaching mode. Then, gradients are set to zero to forestall accumulation from earlier steps. The mannequin predicts the output for the graph, and the loss is calculated. Backpropagation then computes the gradients, and the optimizer step updates the mannequin’s weights. Then, the loss for that epoch is recorded. After coaching, the operate returns the educated mannequin and the checklist of losses over epochs.
def train_model(knowledge, epochs=200, lr=0.01):
mannequin = GCN(input_dim=knowledge.num_node_features, hidden_dim=32)
optimizer = torch.optim.Adam(mannequin.parameters(), lr=lr)
losses = []for epoch in vary(epochs):
mannequin.prepare()
optimizer.zero_grad()
out = mannequin(knowledge)
loss = F.mse_loss(out, knowledge.y)
loss.backward()
optimizer.step()
losses.append(loss.merchandise())
return mannequin, losses
Visualization
Following the coaching course of, completely different visualizations may be made to investigate its effectiveness and predictions.
One such plot that may be utilized to see how the mannequin’s efficiency improves over time is the coaching loss plot. The x-axis is the variety of epochs, and the y-axis is the MSE loss. A reducing loss curve signifies that the mannequin is studying to make higher predictions.
plt.plot(losses)
plt.title("Coaching Loss Curve")
plt.xlabel("Epoch")
plt.ylabel("MSE Loss")
plt.grid(True)
plt.present()
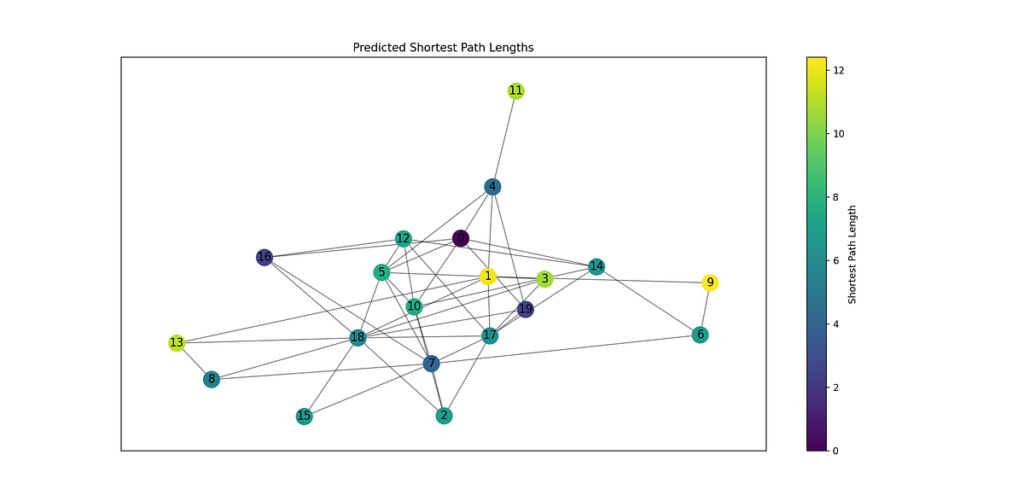
Graph visualizations may also be made to guage the mannequin’s predictions compared to the precise graph. The sprint_layout algorithm is used to place the nodes in a visually interesting manner, and the colour of every node is set by both the true shortest path size or the anticipated shortest path size.
def plot_graph(G, y_true, y_pred=None, title="Graph"):
pos = nx.spring_layout(G, seed=42)
plt.determine(figsize=(10, 8))color_map = y_pred if y_pred will not be None else y_true
nodes = nx.draw_networkx_nodes(G, pos, node_color=color_map, cmap=plt.cm.viridis, node_size=300)
nx.draw_networkx_edges(G, pos, alpha=0.5)
nx.draw_networkx_labels(G, pos)
plt.title(title)
plt.colorbar(nodes, label="Shortest Path Size")
plt.present()
Placing Every little thing Collectively
On the finish of the script, a random graph may be generated and transformed into PyTorch Geometric format. Then, the mannequin is educated and evaluated, with predictions made with torch.no_grad() to keep away from computing gradients. The coaching loss curve is then plotted to observe mannequin enchancment over epochs. Lastly, two visualizations of the graph are plotted: the shortest path lengths and the anticipated shortest path lengths, to point out how shut the mannequin’s predictions are to the precise values.
G = generate_graph()
knowledge, nx_graph = graph_to_data(G, source_node=0)
mannequin, losses = train_model(knowledge)mannequin.eval()
with torch.no_grad():
pred = mannequin(knowledge)
plt.plot(losses)
plt.title("Coaching Loss Curve")
plt.xlabel("Epoch")
plt.ylabel("MSE Loss")
plt.grid(True)
plt.present()
plot_graph(nx_graph, knowledge.y.numpy(), title="Floor Fact Shortest Path Lengths")
plot_graph(nx_graph, knowledge.y.numpy(), title="Predicted Shortest Path Lengths")
The truth that the precise shortest path lengths and the anticipated values are practically equivalent demonstrates how efficient GCNs are in capturing the underlying constructions of the graph. The mannequin efficiently leverages the graph’s options to foretell the shortest paths with excessive accuracy. This means that GCNs are usually not solely able to studying from native graph data but additionally generalizing effectively to unseen elements of the graph.
Graph Neural Networks signify a robust and scalable methodology for fixing a myriad of graph principle issues. By leveraging the graph construction straight via message passing and neighborhood aggregation, GNNs can resolve advanced issues like shortest path and TSP with higher flexibility than classical algorithms. The flexibility of GNNs to course of giant and sophisticated graphs with out the necessity for specific characteristic engineering makes them significantly highly effective for real-world functions.
As demonstrated within the sensible implementation, using GNNs can result in extremely correct predictions of the shortest paths, reflecting the community’s skill to generalize throughout unseen graph constructions. This skill opens up new potentialities for optimizing community flows, analyzing completely different constructions, and tackling issues in logistics and routing extra successfully.
Wanting ahead, as GNNs proceed to evolve and enhance with developments in computational energy and algorithmic improvements, their potential to revolutionize graph principle issues turns into more and more clear. With functions spanning throughout numerous industries from healthcare to social media, GNNs are poised to change into a elementary instrument for researchers working with graph-based knowledge.