In my skilled life as a knowledge scientist, I’ve encountered time sequence a number of instances. Most of my information comes from my educational expertise, particularly my programs in Econometrics (I’ve a level in Economics), the place we studied statistical properties and fashions of time sequence.
Among the many fashions I studied was SARIMA, which acknowledges the seasonality of a time sequence, nonetheless, we’ve by no means studied find out how to intercept and acknowledge seasonality patterns.
More often than not I needed to discover seasonal patterns I merely relied on visible inspections of information. This was till I came upon this YouTube video on Fourier transforms and ultimately discovered what a periodogram is.
On this weblog publish, I’ll clarify and apply easy ideas that may flip into helpful instruments that each DS who’s learning time sequence ought to know.
Desk of Contents
- What’s a Fourier Remodel?
- Fourier Remodel in Python
- Periodogram
Overview
Let’s assume I’ve the next dataset (AEP energy consumption, CC0 license):
import pandas as pd
import matplotlib.pyplot as plt
df = pd.read_csv("information/AEP_hourly.csv", index_col=0)
df.index = pd.to_datetime(df.index)
df.sort_index(inplace=True)
fig, ax = plt.subplots(figsize=(20,4))
df.plot(ax=ax)
plt.tight_layout()
plt.present()It is vitally clear, simply from a visible inspection, that seasonal patterns are enjoying a task, nonetheless it is perhaps trivial to intercept all of them.
As defined earlier than, the invention course of I used to carry out was primarily handbook, and it might have appeared one thing as follows:
fig, ax = plt.subplots(3, 1, figsize=(20,9))
df_3y = df[(df.index >= '2006–01–01') & (df.index < '2010–01–01')]
df_3M = df[(df.index >= '2006–01–01') & (df.index < '2006–04–01')]
df_7d = df[(df.index >= '2006–01–01') & (df.index < '2006–01–08')]
ax[0].set_title('AEP power consumption 3Y')
df_3y[['AEP_MW']].groupby(pd.Grouper(freq = 'D')).sum().plot(ax=ax[0])
for date in df_3y[[True if x % (24 * 365.25 / 2) == 0 else False for x in range(len(df_3y))]].index.tolist():
ax[0].axvline(date, colour = 'r', alpha = 0.5)
ax[1].set_title('AEP power consumption 3M')
df_3M[['AEP_MW']].plot(ax=ax[1])
for date in df_3M[[True if x % (24 * 7) == 0 else False for x in range(len(df_3M))]].index.tolist():
ax[1].axvline(date, colour = 'r', alpha = 0.5)
ax[2].set_title('AEP power consumption 7D')
df_7d[['AEP_MW']].plot(ax=ax[2])
for date in df_7d[[True if x % 24 == 0 else False for x in range(len(df_7d))]].index.tolist():
ax[2].axvline(date, colour = 'r', alpha = 0.5)
plt.tight_layout()
plt.present()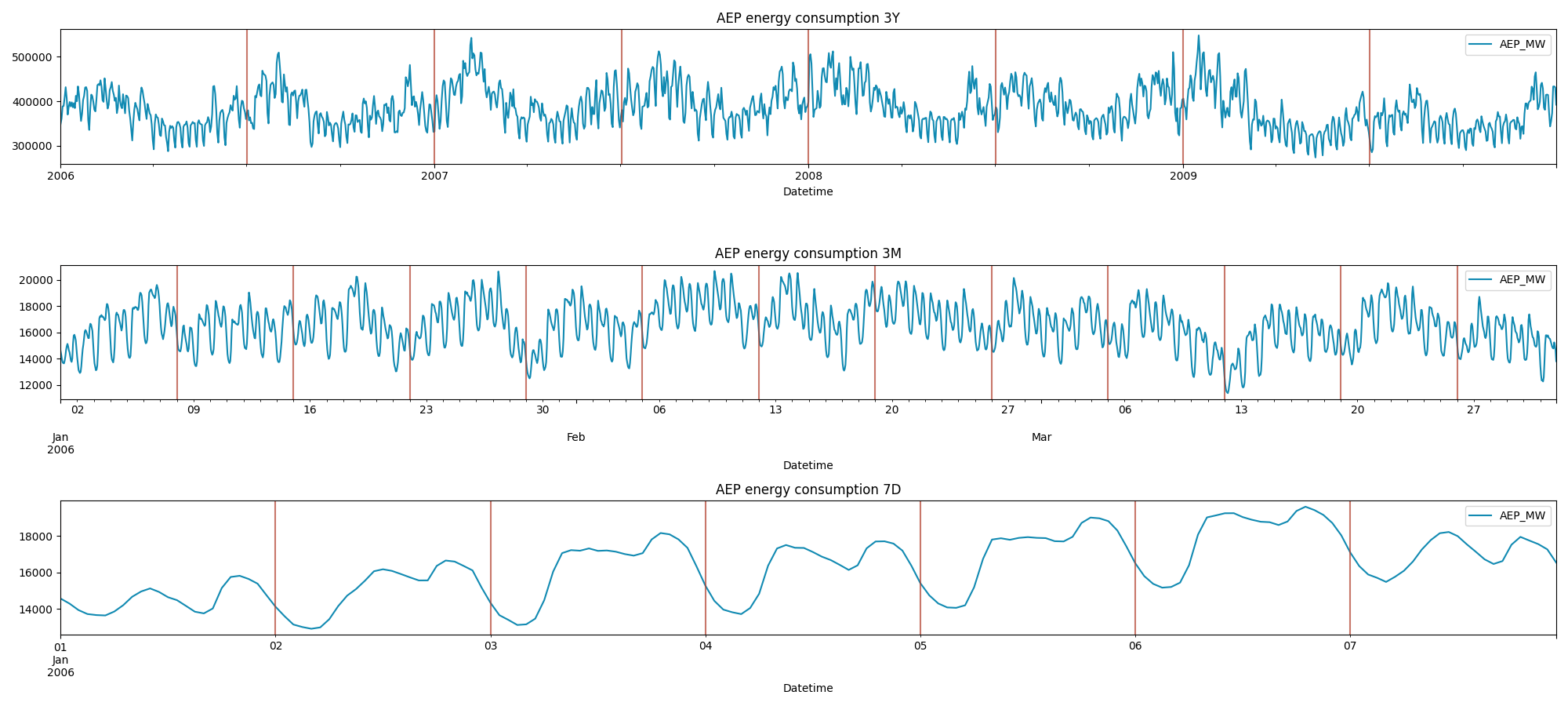
It is a extra in-depth visualization of this time sequence. As we are able to see the next patterns are influencing the information: **- a 6 month cycle,
- a weekly cycle,
- and a day by day cycle.**
This dataset exhibits power consumption, so these seasonal patterns are simply inferable simply from area information. Nevertheless, by relying solely on a handbook inspection we might miss necessary informations. These may very well be a number of the predominant drawbacks:
- Subjectivity: We would miss much less apparent patterns.
- Time-consuming : We have to check totally different timeframes one after the other.
- Scalability points: Works effectively for just a few datasets, however inefficient for large-scale evaluation.
As a Knowledge Scientist it might be helpful to have a software that provides us rapid suggestions on crucial frequencies that compose the time sequence. That is the place the Fourier Transforms come to assist.
1. What’s a Fourier Remodel
The Fourier Remodel is a mathematical software that enables us to “change area”.
Normally, we visualize our information within the time area. Nevertheless, utilizing a Fourier Remodel, we are able to change to the frequency area, which exhibits the frequencies which are current within the sign and their relative contribution to the unique time sequence.
Instinct
Any well-behaved operate f(x) may be written as a sum of sinusoids with totally different frequencies, amplitudes and phases. In easy phrases, each sign (time sequence) is only a mixture of easy waveforms.
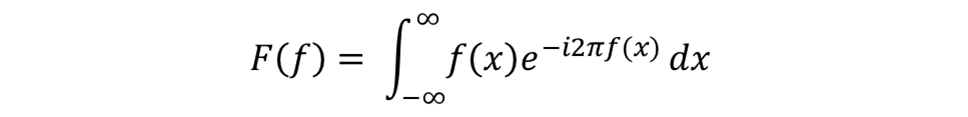
The place:
- F(f) represents the operate within the frequency area.
- f(x) is the unique operate within the time area.
- exp(−i2πf(x)) is a posh exponential that acts as a “frequency filter”.
Thus, F(f) tells us how a lot frequency f is current within the unique operate.
Instance
Let’s think about a sign composed of three sine waves with frequencies 2 Hz, 3 Hz, and 5 Hz:
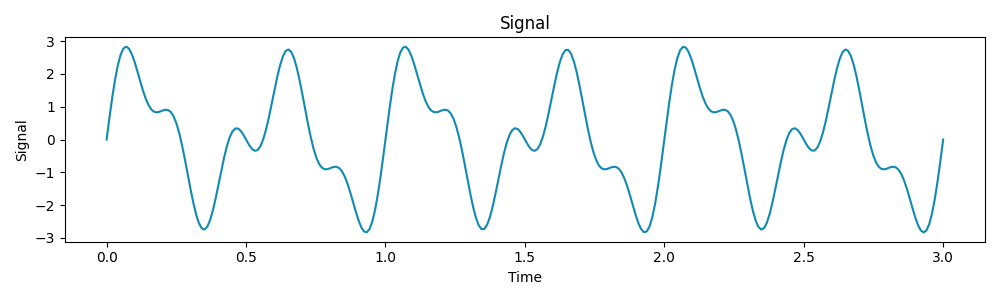
Now, let’s apply a Fourier Remodel to extract these frequencies from the sign:
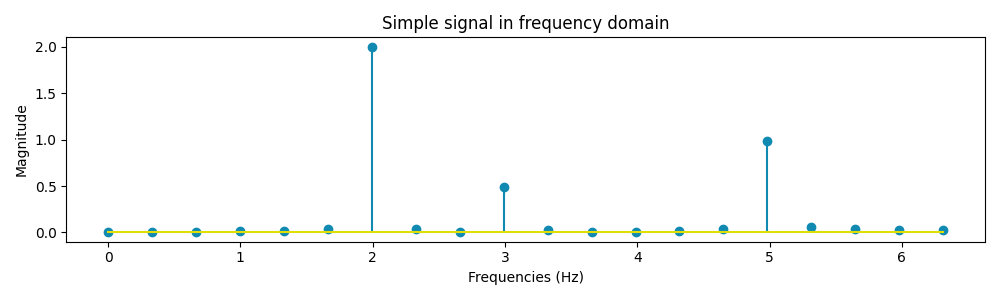
The graph above represents our sign expressed within the frequency area as an alternative of the basic time area. From the ensuing plot, we are able to see that our sign is decomposed in 3 parts of frequency 2 Hz, 3 Hz and 5 Hz as anticipated from the beginning sign.
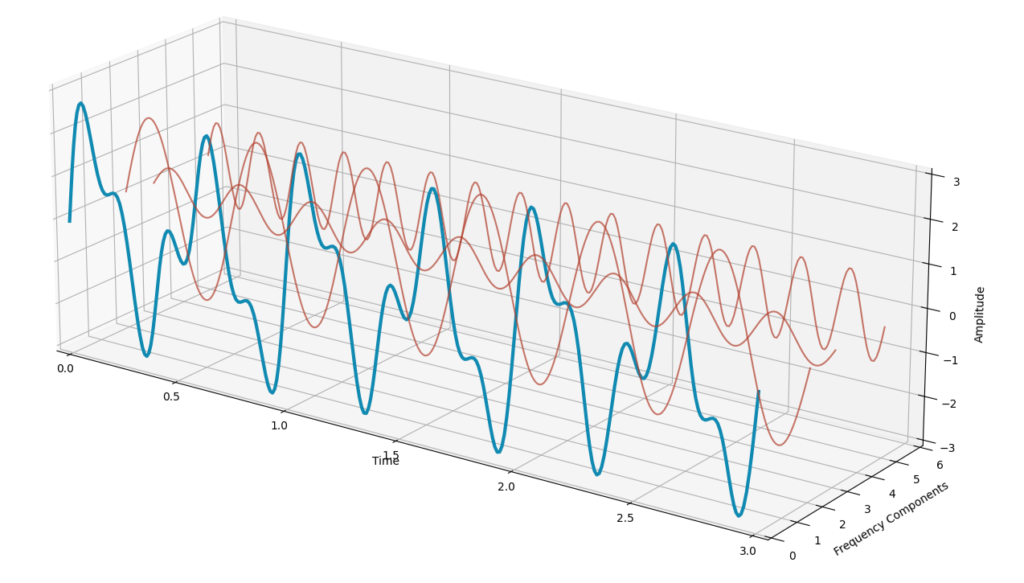
As stated earlier than, any well-behaved operate may be written as a sum of sinusoids. With the data we’ve up to now it’s potential to decompose our sign into three sinusoids:
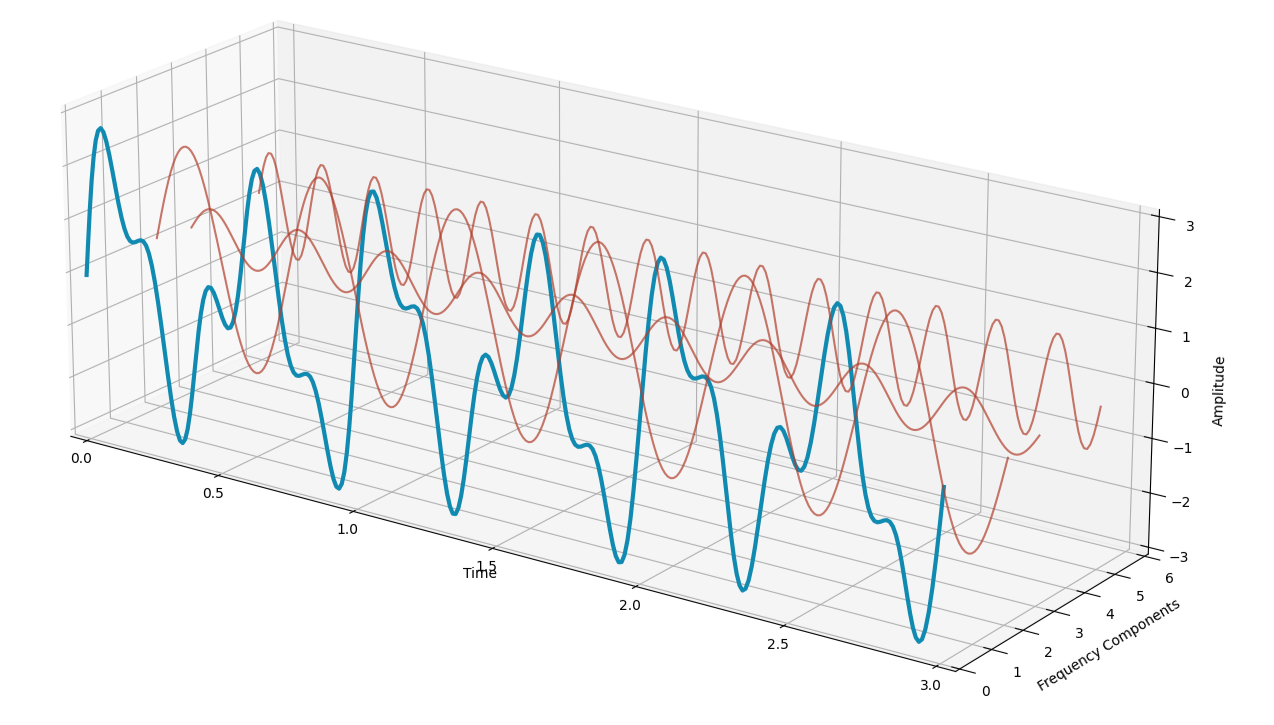
The unique sign (in blue) may be obtained by summing the three waves (in purple). This course of can simply be utilized in any time sequence to guage the primary frequencies that compose the time sequence.
2 Fourier Remodel in Python
Provided that it’s fairly simple to change between the time area and the frequency area, let’s take a look on the AEP power consumption time sequence we began learning firstly of the article.
Python gives the “numpy.fft” library to compute the Fourier Remodel for discrete indicators. FFT stands for Quick Fourier Remodel which is an algorithm used to decompose a discrete sign into its frequency parts:
from numpy import fft
X = fft.fft(df['AEP_MW'])
N = len(X)
frequencies = fft.fftfreq(N, 1)
intervals = 1 / frequencies
fft_magnitude = np.abs(X) / N
masks = frequencies >= 0
# Plot the Fourier Remodel
fig, ax = plt.subplots(figsize=(20, 3))
ax.step(intervals[mask], fft_magnitude[mask]) # Solely plot constructive frequencies
ax.set_xscale('log')
ax.xaxis.set_major_formatter('{x:,.0f}')
ax.set_title('AEP power consumption - Frequency-Area')
ax.set_xlabel('Frequency (Hz)')
ax.set_ylabel('Magnitude')
plt.present()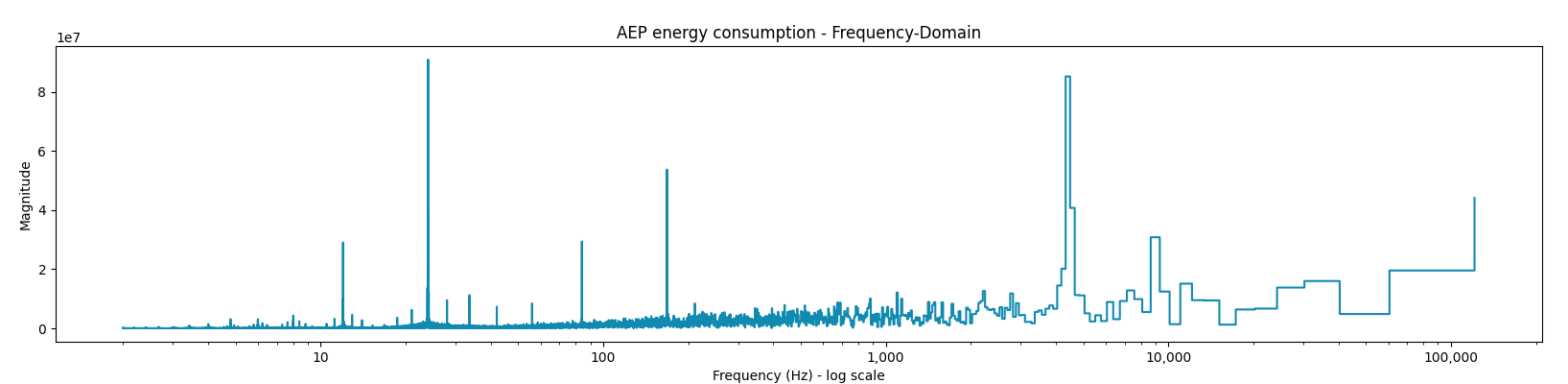
That is the frequency area visualization of the AEP_MW power consumption. Once we analyze the graph we are able to already see that at sure frequencies we’ve the next magnitude, implying larger significance of such frequencies.
Nevertheless, earlier than doing so we add yet one more piece of idea that may permit us to construct a periodogram, that may give us a greater view of crucial frequencies.
3. Periodogram
The periodogram is a frequency-domain illustration of the energy spectral density (PSD) of a sign. Whereas the Fourier Remodel tells us which frequencies are current in a sign, the periodogram quantifies the facility (or depth) of these frequencies. This passage is usefull because it reduces the noise of much less necessary frequencies.
Mathematically, the periodogram is given by:
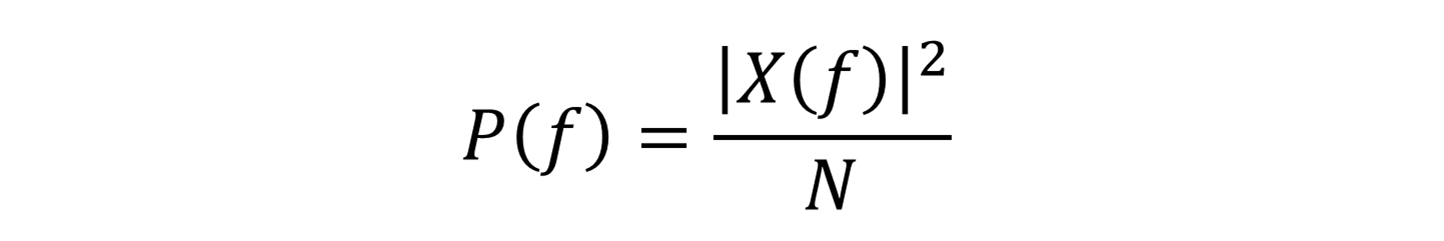
The place:
- P(f) is the facility spectral density (PSD) at frequency f,
- X(f) is the Fourier Remodel of the sign,
- N is the full variety of samples.
This may be achieved in Python as follows:
power_spectrum = np.abs(X)**2 / N # Energy at every frequency
fig, ax = plt.subplots(figsize=(20, 3))
ax.step(intervals[mask], power_spectrum[mask])
ax.set_title('AEP power consumption Periodogram')
ax.set_xscale('log')
ax.xaxis.set_major_formatter('{x:,.0f}')
plt.xlabel('Frequency (Hz)')
plt.ylabel('Energy')
plt.present()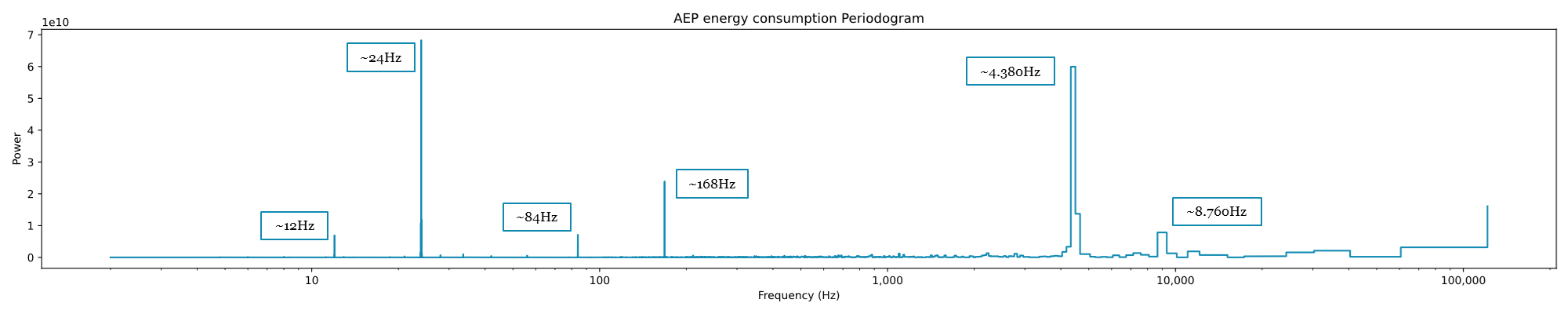
From this periodogram, it’s now potential to draw conclusions. As we are able to see essentially the most highly effective frequencies sit at:
- 24 Hz, similar to 24h,
- 4.380 Hz, corresponding to six months,
- and at 168 Hz, similar to the weekly cycle.
These three are the identical Seasonality parts we discovered within the handbook train accomplished within the visible inspection. Nevertheless, utilizing this visualization, we are able to see three different cycles, weaker in energy, however current:
- a 12 Hz cycle,
- an 84 Hz cycle, correspondint to half per week,
- an 8.760 Hz cycle, similar to a full yr.
It’s also potential to make use of the operate “periodogram” current in scipy to acquire the identical outcome.
from scipy.sign import periodogram
frequencies, power_spectrum = periodogram(df['AEP_MW'], return_onesided=False)
intervals = 1 / frequencies
fig, ax = plt.subplots(figsize=(20, 3))
ax.step(intervals, power_spectrum)
ax.set_title('Periodogram')
ax.set_xscale('log')
ax.xaxis.set_major_formatter('{x:,.0f}')
plt.xlabel('Frequency (Hz)')
plt.ylabel('Energy')
plt.present()Conclusions
Once we are coping with time sequence one of the vital necessary parts to think about is seasonalities.
On this weblog publish, we’ve seen find out how to simply uncover seasonalities inside a time sequence utilizing a periodogram. Offering us with a simple-to-implement software that may turn into extraordinarily helpful within the exploratory course of.
Nevertheless, that is simply a place to begin of the potential implementations of Fourier Remodel that we may benefit from, as there are a lot of extra:
- Spectrogram
- Function encoding
- Time sequence decomposition
- …
Please depart some claps when you loved the article and be happy to remark, any suggestion and suggestions is appreciated!
_Here you can find a notebook with the code from this blog post._
Source link