Right here’s one thing which may shock you: one of the vital necessary steps in knowledge evaluation can also be one of the vital missed. Earlier than you soar into constructing fashions or operating exams, it is advisable perceive what sort of knowledge you’re truly working with.
Give it some thought. In case you had been planning a street journey, you’d in all probability verify the climate forecast first, proper? You wouldn’t pack the identical manner for a sunny seaside trip as you’d for a snowy mountain journey. The identical logic applies to your knowledge. Several types of knowledge name for various analytical approaches, and should you don’t know what you’re coping with, you’re basically packing flip-flops for a blizzard.
But most individuals skip this step totally. They seize their knowledge, throw it into no matter mannequin appears widespread, and hope for the very best. Generally they get fortunate. Extra typically, they get outcomes that look spectacular however don’t truly imply a lot.
When statisticians discuss “distributions,” they’re referring to the underlying sample that describes how your knowledge behaves.
Each dataset has some form of sample — perhaps your values cluster round a central level (like folks’s heights), or perhaps they comply with a steep drop-off (like earnings distribution), or perhaps they’re fully random (like lottery numbers).
Understanding this sample isn’t simply nerdy curiosity. It tells you which of them statistical instruments will work and which of them provides you with rubbish outcomes. It’s the distinction between utilizing the suitable software for the job and attempting to hammer a screw.
Let’s begin with one thing everybody can perceive — the histogram. You’ve in all probability made these earlier than with out pondering a lot about them, however they’re truly extremely highly effective knowledge instruments.
A histogram is only a bar chart that reveals how typically completely different values seem in your dataset. You divide your knowledge into bins (like age teams 20–30, 30–40, and so forth.) and depend what number of knowledge factors fall into every bin. Easy, however revealing.
Right here’s the factor about histograms — they’ll inform you numerous about what you’re coping with:
- Does it appear like a bell curve? You might need usually distributed knowledge
- Does it begin excessive and drop off rapidly? Might be an exponential distribution
- Is it comparatively flat throughout the board? Is likely to be uniformly distributed
- Does it have a number of peaks? You might be a combination of various teams
Let me present you make one that truly tells you one thing helpful:
import matplotlib.pyplot as plt
import numpy as np# Let's create some pattern knowledge
knowledge = np.random.regular(50, 15, 1000) # 1000 factors, imply=50, std=15
# Make a histogram that is straightforward to learn
plt.determine(figsize=(10, 6))
plt.hist(knowledge, bins=30, shade='skyblue', edgecolor='black', alpha=0.7)
plt.xlabel('Values')
plt.ylabel('Depend')
plt.title('What Does Our Information Look Like?')
plt.grid(True, alpha=0.3)
plt.present()
Now, right here’s a professional tip: should you see a number of peaks in your histogram, strive altering the variety of bins. Actual peaks from precise patterns in your knowledge will stick round even while you change the bin dimension. Faux peaks from random noise will disappear or transfer round.
One of the best ways to grasp distributions is to see them in motion. Use this software to experiment with completely different knowledge patterns and watch how they behave.
What to strive:
- Swap between distribution sorts to see how dramatically shapes can change
- Modify pattern dimension to see when patterns turn into clear vs. noisy
- Change the variety of histogram bins — typically peaks are actual, typically they’re simply artifacts
- Toggle the theoretical match line to see when math matches actuality
Key perception: If the purple fitted curve seems clearly flawed when plotted towards your histogram, belief your eyes over the statistics.
When you’ve acquired a really feel on your knowledge from the histogram, you will get extra rigorous about discovering the very best match. Right here’s how I like to consider it:
Step 1: Get the lay of the land
Make that histogram we simply talked about. This provides you a tough concept of what you’re working with.
Step 2: Attempt on completely different distributions for dimension
That is the place you take a look at your knowledge towards varied theoretical distributions — regular, exponential, gamma, and so forth. For each, you estimate the parameters that will make that distribution suit your knowledge as intently as attainable.
Step 3: Rating how properly each matches
Use statistical exams to get precise numbers on how good every match is. Consider it like a report card for every distribution.
Step 4: Choose your winner
Select the distribution that scores greatest, however don’t simply go together with the numbers — ensure that it is sensible on your particular state of affairs.
Now, you possibly can do all this math by hand, however life’s too brief. There’s a Python library referred to as distfit that does the heavy lifting for you. This is use it:
from distfit import distfit
import numpy as np# As an instance you've gotten some knowledge
my_data = np.random.regular(25, 8, 2000) # 2000 knowledge factors
# Arrange the distribution fitter
fitter = distfit(technique='parametric')
# Let it strive completely different distributions and discover the very best match
fitter.fit_transform(my_data)
# See what it discovered
print("Finest match:", fitter.mannequin['name'])
print("Parameters:", fitter.mannequin['params'])
The cool factor about distfit is that it exams round 90 completely different distributions routinely. It is like having a extremely affected person statistician who’s keen to strive each attainable choice and inform you which one works greatest.
However right here’s the place it will get attention-grabbing.
Let’s say you generated knowledge from a traditional distribution (like within the instance above). You may anticipate the conventional distribution to win, however typically it doesn’t. Why?
Effectively, your knowledge is only a pattern — it’s not good. And a few distributions are versatile sufficient that they’ll mimic different distributions fairly properly. Plus, completely different statistical exams emphasize completely different elements of the match. So don’t panic if the “apparent” selection doesn’t at all times win.
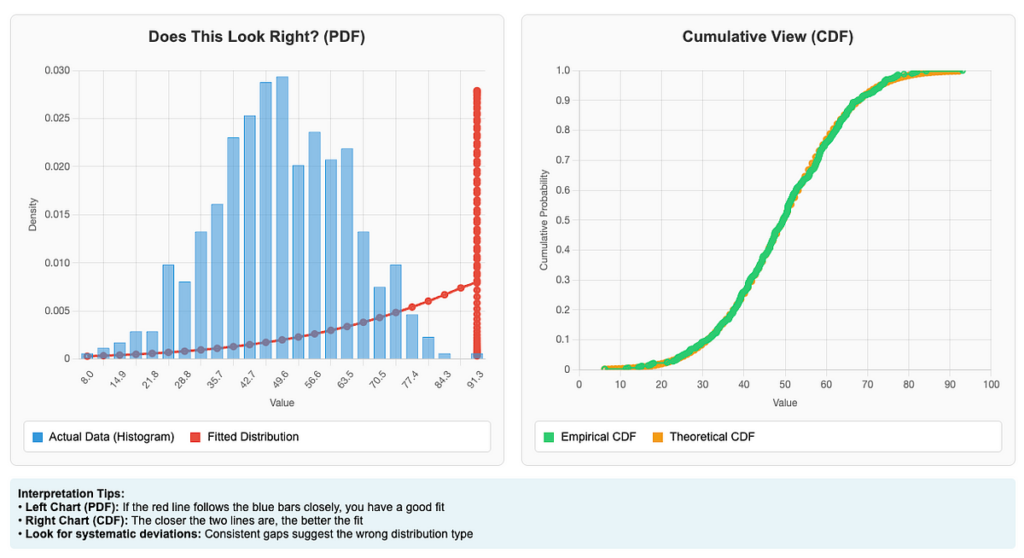
Statistics is nice, however your eyes are necessary too. All the time have a look at the outcomes, don’t simply belief the numbers. Right here’s visualize what you discovered:
import matplotlib.pyplot as plt# Create a few plots to see how properly your distribution matches
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 6))
# Left plot: your knowledge with the fitted curve overlaid
fitter.plot(chart='PDF', ax=ax1)
ax1.set_title('Does This Look Proper?')
# Proper plot: cumulative distribution
fitter.plot(chart='CDF', ax=ax2)
ax2.set_title('Cumulative View')
plt.tight_layout()
plt.present()
If the fitted curve seems prefer it’s doing a superb job following your knowledge, you’re in all probability heading in the right direction. If it seems manner off, you may have to strive a special method.
Generally your knowledge simply received’t match any normal distribution. Possibly it’s too bizarre, too messy, or has a number of peaks. That’s the place non-parametric strategies come in useful.
As a substitute of attempting to power your knowledge right into a pre-defined form, these strategies let the information converse for itself:
# For knowledge that does not match normal patterns
flexible_fitter = distfit(technique='quantile')
flexible_fitter.fit_transform(my_data)# Or do this method
percentile_fitter = distfit(technique='percentile')
percentile_fitter.fit_transform(my_data)
These strategies are extra versatile however offer you much less particular details about the underlying sample. It’s a trade-off.
In case your knowledge is counts (variety of web site visits, variety of defects, variety of buyer complaints), you want a special method. You’re coping with discrete knowledge, not steady knowledge.
from scipy.stats import binom# Generate some depend knowledge for testing
n_trials = 20
success_rate = 0.3
count_data = binom(n_trials, success_rate).rvs(1000)
# Match discrete distributions
discrete_fitter = distfit(technique='discrete')
discrete_fitter.fit_transform(count_data)
# See the way it did
discrete_fitter.plot()
Right here’s one thing necessary: simply since you discovered a distribution that matches doesn’t imply it’s the suitable one on your functions. It’s essential to validate your selection.
A technique to do that is bootstrapping — principally, you are taking random samples out of your fitted distribution and see in the event that they appear like your authentic knowledge:
# Check the steadiness of your match
fitter.bootstrap(my_data, n_boots=100)# Test the outcomes
print(fitter.abstract[['name', 'score', 'bootstrap_score', 'bootstrap_pass']])
In case your chosen distribution retains performing properly throughout completely different bootstrap samples, you might be extra assured in your selection.
As soon as you already know your knowledge’s distribution, you may:
- Spot outliers extra successfully: If you already know what “regular” seems like on your knowledge, uncommon factors stand out extra clearly.
- Generate life like pretend knowledge: Want to check your evaluation with extra knowledge? Generate artificial knowledge that follows the identical sample as your actual knowledge.
- Select higher fashions: Many statistical fashions work greatest with sure kinds of knowledge. Understanding your distribution helps you decide the suitable software.
- Make higher predictions: Understanding the underlying sample helps you make extra correct forecasts about future knowledge.
After doing this sort of evaluation for some time, listed here are some issues I’ve realized:
Don’t simply go together with no matter will get the very best rating.
Take into consideration whether or not the distribution is sensible on your knowledge. In case you’re human heights, a traditional distribution is sensible. In case you’re time between failures, an exponential could be extra acceptable.
All the time have a look at the plots. Numbers can lie, however your eyes often don’t. If the fitted curve seems flawed, it in all probability is.
Do not forget that all fashions are flawed, however some are helpful. You’re not looking for the “true” distribution — you’re looking for a helpful approximation that helps you perceive your knowledge higher.
Don’t overthink it. Generally a easy method works higher than a sophisticated one.
If a traditional distribution matches your knowledge fairly properly and is sensible on your context, you don’t want to search out one thing extra unique.
Distribution becoming may appear to be plenty of work, but it surely’s price it. It’s the inspiration that every part else builds on. Get this proper, and your analyses will probably be extra correct, your fashions will carry out higher, and your conclusions will probably be extra dependable.
The instruments I’ve proven you right here will deal with most conditions you’ll encounter. Begin with histograms to get a really feel on your knowledge, use distfit to check completely different distributions systematically, and at all times validate your outcomes each statistically and visually.
Bear in mind, the aim isn’t to search out the right distribution — it’s to search out one which’s adequate on your functions and helps you perceive your knowledge higher. Generally that’s a easy regular distribution, typically it’s one thing extra advanced, and typically it’s a non-parametric method that doesn’t assume any explicit form.
The secret’s to be systematic about it, belief your instruments however confirm together with your eyes, and at all times hold your particular context in thoughts. Your knowledge has a narrative to inform — distribution becoming helps you hearken to it correctly.