Speculation testing is a basic idea in statistics, enabling knowledge scientists and researchers to make knowledgeable choices based mostly on pattern knowledge. It includes evaluating a speculation a couple of inhabitants parameter utilizing pattern knowledge and figuring out the probability that the speculation is true. This course of is essential in varied fields, together with healthcare, economics, and social sciences, to validate assumptions and information decision-making.
Speculation testing is a statistical technique that makes use of pattern knowledge to judge a speculation a couple of inhabitants parameter. The method includes two competing hypotheses:
- Null Speculation (H₀): Assumes no impact or no distinction.
- Different Speculation (H₁): Contradicts the null speculation, suggesting an impact or distinction.
The purpose is to find out whether or not there may be sufficient statistical proof to reject the null speculation in favour of the choice speculation.
In knowledge science, speculation testing permits professionals to:
- Validate Fashions: Assess the effectiveness of predictive fashions.
- Make Selections: Inform enterprise methods and choices.
- Guarantee Accuracy: Verify that noticed patterns aren’t resulting from random probability.
By systematically testing hypotheses, knowledge scientists can draw dependable conclusions and make data-driven choices.
- P-Worth: The chance of acquiring outcomes not less than as excessive because the outcomes truly noticed, below the idea that the null speculation is right. A smaller p-value signifies stronger proof towards the null speculation. A really in-depth article on p-value: InDepth P Value
- Significance Degree (α): A threshold set by the researcher (generally 0.05) under which the null speculation is rejected. If the p-value is lower than α, the null speculation is rejected.
- Kind I Error (False Optimistic): Incorrectly rejecting the null speculation when it’s truly true.
- Kind II Error (False Unfavourable): Failing to reject the null speculation when it’s truly false.
Balancing these errors is essential in speculation testing to make sure dependable conclusions.
Lets attempt to perceive What is definitely p Worth?
You’re a researcher testing whether or not Drug A helps cut back blood strain.
- You are taking a pattern of fifty sufferers.
- You give Drug A to those sufferers for 4 weeks.
- You measure their blood strain earlier than and after.
- You discover that their common blood strain decreased.
Now, you wish to check:
Is that this enchancment resulting from Drug A, or may it have occurred simply by random probability?
- Null Speculation (H₀):
Drug A has no impact on blood strain. (Any change is simply resulting from probability.) - Different Speculation (H₁):
Drug A has a constructive impact on blood strain (it reduces it).
After doing all of your statistical check (say, a paired t-test, because you’re evaluating before-and-after values in the identical group), you get a p-value.
Let’s say your p-value is 0.03.
A p-value of 0.03 means:
If Drug A truly had no impact (i.e., if H₀ is true), there’s solely a 3% probability you’d see this a lot enchancment simply by random probability.
In less complicated phrases:
You’re asking, “If Drug A doesn’t actually work, how seemingly is it that I’d nonetheless see these outcomes?”
The p-value tells you that chance.
- Low p-value = Sturdy proof towards H₀ (i.e., it helps your alternate speculation).
- Excessive p-value = Weak proof towards H₀ (you’ll be able to’t conclude Drug A works).
- p-value does NOT let you know the scale of the impact, solely how seemingly the noticed impact is below the null speculation.
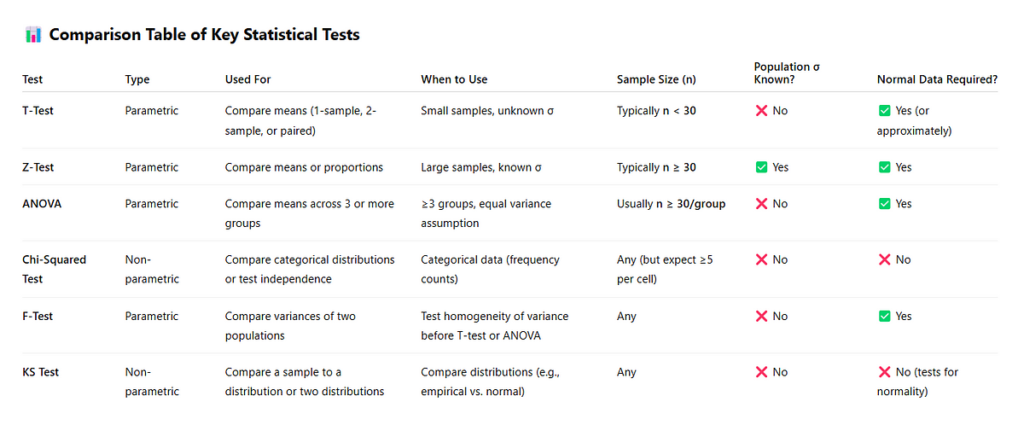
- Use Case: When the pattern dimension is giant (n ≥ 30) and the inhabitants variance is understood.
- Instance: An organization claims that their common product lifespan is 5 years. A pattern of 100 merchandise is examined, and the common lifespan is discovered to be 4.8 years. A z-test can decide if this distinction is statistically important.
- Use Case: When the pattern dimension is small (n < 30) or the inhabitants variance is unknown.
- One-Pattern T-Check: Compares the pattern imply to a identified worth.
- Two-Pattern T-Check: Compares the technique of two impartial teams.
- Paired T-Check: Compares means from the identical group at completely different instances.
- Use Case: When evaluating means throughout three or extra teams.
- Instance: A research compares the effectiveness of three completely different diets on weight reduction. ANOVA can decide if there are any statistically important variations between the food regimen teams.
- Use Case: For categorical knowledge to evaluate how noticed frequencies evaluate to anticipated frequencies.
- Instance: A survey examines the connection between gender and choice for a brand new product. A chi-square check can decide if there may be an affiliation between the 2 variables.
Instance State of affairs on Find out how to use T-Check & Z-Check?
Drawback Assertion
Marine biologists imagine that the common weight of grownup sharks in a sure ocean area is 198 kg. To check this perception, a researcher collects a random pattern of 100 sharks and finds that:
- the pattern imply weight is 200 kg,
- the pattern normal deviation is 2.31 kg.
Assuming the weights are usually distributed: