Understanding the Math Behind the Magic — How Larger-Order Derivatives Form Optimization, Regularization, and Interpretability in Neural Networks
Discover how Jacobians and Hessians affect mannequin coaching, generalization, and explainability — full with PyTorch Autograd code examples.
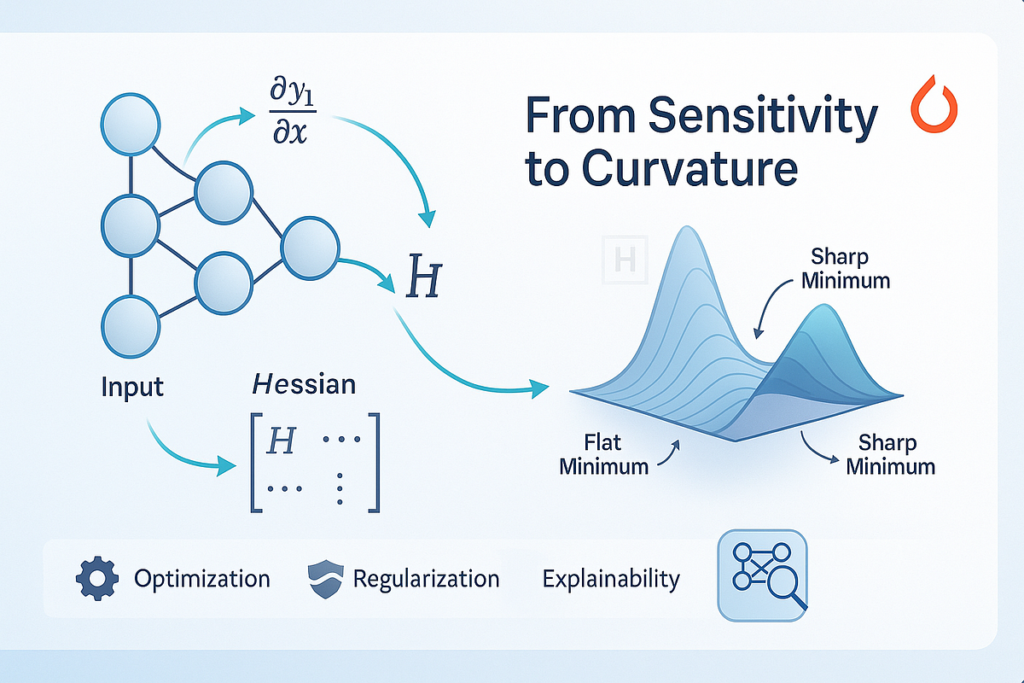
Whenever you prepare a neural community, you’re tuning thousands and thousands of parameters. You’re hoping they study to “see,” “hear,” or “perceive” higher with every epoch. However beneath the hood, it’s not simply gradients (first derivatives) that form the training course of — it’s the higher-order derivatives that refine, regularize, and reveal.
In a world obsessive about deep fashions and enormous datasets, understanding the Jacobian and Hessian matrices provides us a lens into the sensitivity, curvature, and internal construction of those fashions. They inform us not simply how briskly issues are altering (gradient), however how the speed of change is altering — and that’s vital in optimizing deep studying algorithms which can be usually brittle, overfitted, or uninterpretable.
Let’s break down why the Jacobian and Hessian aren’t simply mathematical formalities however…