Think about you’re at a farmers’ market, eyeing a fruit that appears like an apple however has the feel of an orange. To determine what it’s, you ask the seller, “What’s the closest match to this fruit?” That is the essence of the Okay-Nearest Neighbors (Okay-NN) algorithm! On this weblog of my Okay-NN sequence, we’ll break down how Okay-NN classifies information, its geometric instinct, and the mathematics behind measuring similarity. Let’s dive in!
Okay-NN classifies information factors by majority vote of their closest neighbors. Right here’s the way it works:
- Step 1: Select a quantity Okay (e.g., Okay=3).
- Step 2: Calculate distances between the brand new information level and all coaching factors.
- Step 3: Determine the Okay closest neighbors.
- Step 4: Assign the bulk class amongst these neighbors.
Instance:
Suppose we’ve got fruits with two options: weight (grams) and sweetness (1–10 scale):
- Apples: Heavy (150g) and candy (8/10).
- Oranges: Mild (100g) and tangy (3/10).
A brand new fruit at 130g, 6/10 sweetness is in comparison with its neighbors. If 2 of the three closest fruits are apples, it’s categorised as an apple.
Knowledge in Okay-NN is structured as an n x m matrix:
- Rows: Situations (e.g., fruits).
- Columns: Options (e.g., weight, sweetness) + Label.
Fruit_ID | Weight (g) | Sweetness (1-10) | Label
1 150 8 Apple
2 100 3 Orange
3 130 6 ???
- Classification: Predicts classes (e.g., spam vs. not spam).
- Regression: Predicts numerical values (e.g., home value = $450K).
Examples:
Classification: Diagnose a tumor as benign/malignant.
Regression: Predict a affected person’s restoration time in days.
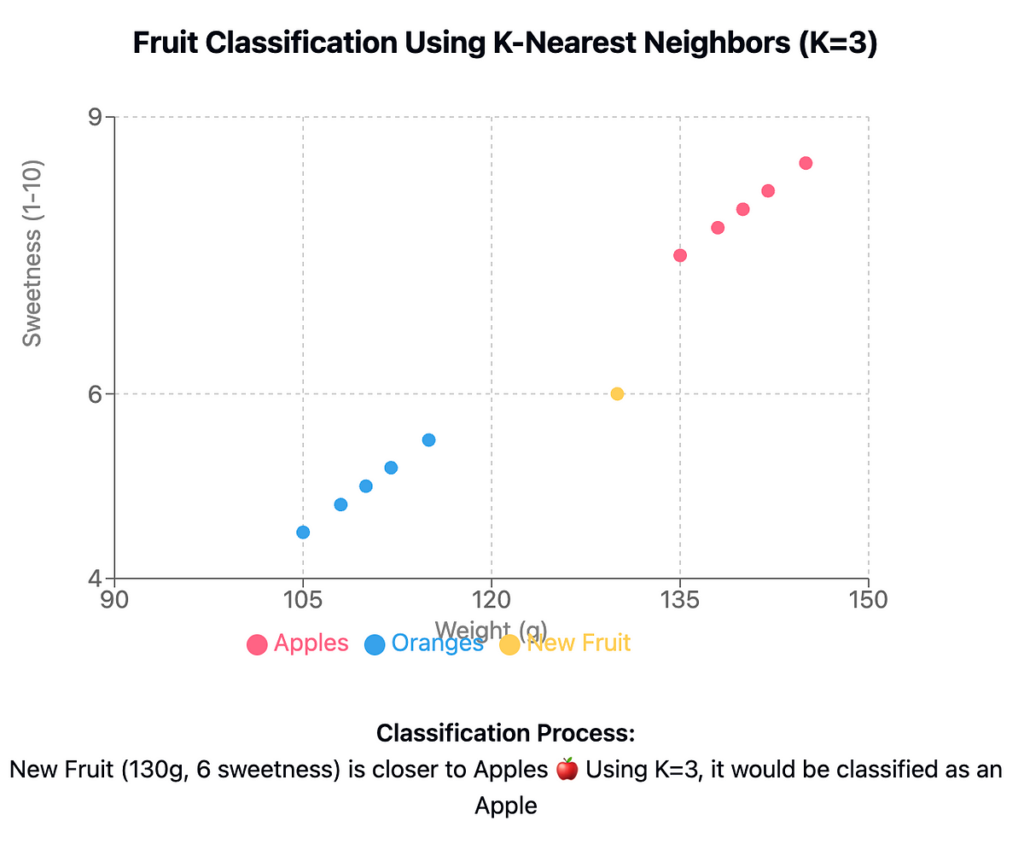
Visualize information on a 2D aircraft:
- X-axis: Weight (g).
- Y-axis: Sweetness (1–10).
- Plot: Apples 🍎 (top-right cluster) and Oranges 🍊 (bottom-left cluster).
A brand new fruit at (130, 6) lies nearer to apples, so Okay=3 classifies it as an apple.
Okay-NN struggles with:
- Excessive-dimensional information: Distances lose which means (curse of dimensionality).
- Imbalanced courses: A dominant class skews votes (e.g., 100 apples vs. 5 oranges).
- Noisy information: Outliers mislead neighbors (e.g., a “candy” orange within the apple cluster).
Select the suitable measure on your information:
- Euclidean (L2):
- Straight-line distance.
- Method:
√[(x₂ - x₁)² + (y₂ - y₁)²]. - Instance: Distance between (150, 8) and (130, 6) = √[(20)² + (2)²] ≈ 20.1.
2. Manhattan (L1):
- Grid-like path distance.
- Method:
|x₂ - x₁| + |y₂ - y₁|. - Instance: Distance = |20| + |2| = 22.
3. Minkowski:
- Generalizes L1 and L2.
- Method:
(Σ|xᵢ - yᵢ|ᵖ)^(1/p).
4. Hamming:
- For categorical information (counts mismatches).
- Instance: “apple” vs “appel” → Distance = 1.
- Cosine Similarity: Measures the angle between vectors (ideally suited for textual content).
- Method:
(A · B) / (||A|| ||B||). - Instance: Evaluate two textual content paperwork:
- Doc 1: [3, 2, 1] (phrase counts for “AI,” “information,” “code”).
- Doc 2: [1, 2, 3] → Similarity = (31 + 22 + 1*3) / (√14 * √14) ≈ 0.71.
- Cosine Distance:
1 - Cosine Similarity.
from sklearn.neighbors import KNeighborsClassifier
import numpy as np # Coaching information: [Weight, Sweetness]
X_train = np.array([[150, 8], [100, 3], [120, 5], [140, 7]])
y_train = np.array(["Apple", "Orange", "Apple", "Apple"])
# New fruit to categorise
new_fruit = np.array([[130, 6]])
# Okay=3 mannequin with Euclidean distance
mannequin = KNeighborsClassifier(n_neighbors=3, metric='euclidean')
mannequin.match(X_train, y_train)
# Predict
prediction = mannequin.predict(new_fruit)
print(f"Prediction: {prediction[0]}") # Output: "Apple"
- Okay-NN classifies information by evaluating it to the closest coaching examples.
- Distance metrics (Euclidean, Manhattan, and so on.) outline “closeness.”
- Keep away from utilizing Okay-NN for high-dimensional or noisy datasets.
#MachineLearning #DataScience #KNN #AI #Classification