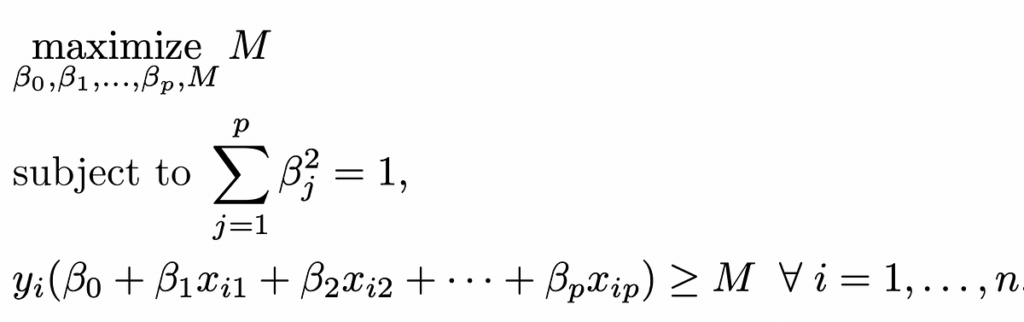SVM Algorithm
Suppose that it’s doable to assemble a hyperplane that separates the coaching observations completely in line with their class labels. We will label the observations from the blue class as yi = 1 and people from the purple class as yi = −1. Then a separating hyperplane has the property that
β0 + β1xi1 + β2xi2 + ··· + βpxip > 0 if yi = 1 and
β0 + β1xi1 + β2xi2 + ··· + βpxip < 0 if yi = −1.
Equivalently, a separating hyperplane has the property that yi(β0 + β1xi1 + β2xi2 + ··· + βpxip) > 0
A pure alternative is the maximal margin hyperplane (often known as the optimum separating hyperplane), which is the separating hyperplane that optimum separating hyperplane is farthest from the coaching observations.
we see that observations that belong to 2 lessons should not essentially separable by a hyperplane. The truth is, even when a separating hyperplane does exist, then there are situations during which a classifer primarily based on a separating hyperplane won’t be fascinating. A classifer primarily based on a separating hyperplane will essentially completely classify all the coaching observations; this will result in sensitivity to particular person observations.
The assist vector classifer, generally known as a delicate margin classifer, assist vector classifer does precisely this. Slightly than looking for the biggest doable margin so that each commentary is just not solely on the proper aspect of the hyperplane but additionally on the proper aspect of the margin, we as a substitute enable some observations to be on the wrong aspect of the margin, and even the wrong aspect of the hyperplane.
the place C is a nonnegative tuning parameter. M is the width of the margin; we search to make this amount as giant as doable. e1,…, en are slack variables that enable particular person observations to be on slack variable the improper aspect of the margin or the hyperplane.
If ei = 0 then the ith commentary is on the proper aspect of the margin. If ei > 0 then the ith commentary is on the improper aspect of the margin, and we are saying that the ith commentary has violated the margin. If ei > 1 then it’s on the improper aspect of the hyperplane.
C is handled as a tuning parameter that’s typically chosen through cross-validation. As with the tuning parameters that we have now seen, C controls the bias-variance trade-of of the statistical studying approach. When C is small, we search slender margins which are hardly ever violated; this quantities to a classifer that’s extremely ft to the info, which can have low bias however excessive variance. However, when C is bigger, the margin is wider and we enable extra violations to it; this quantities to ftting the info much less arduous and acquiring a classifer that’s probably extra biased however could have decrease variance
Why does this result in a non-linear determination boundary?
Within the enlarged characteristic house, the choice boundary that outcomes from is the truth is linear. However within the authentic characteristic house, the choice boundary is of the shape q(x)=0, the place q is a quadratic polynomial, and its options are typically non-linear. One would possibly moreover need to enlarge the characteristic house with higher-order polynomial phrases, or with interplay phrases of the shape XjXj’ for j != j’
One-Versus-One Classifcation
Suppose that we want to carry out classifcation utilizing SVMs, and there are Okay > 2 lessons. A one-versus-one or all-pairs method constructs ‘Okay 2 ( one-versusSVMs, every of which compares a pair of lessons. For instance, one such one SVM would possibly evaluate the kth class, coded as +1, to the ok$ th class, coded as −1. We classify a check commentary utilizing every of the ‘Okay 2 ( classifers, and we tally the variety of instances that the check commentary is assigned to every of the Okay lessons. The fnal classifcation is carried out by assigning the check commentary to the category to which it was most steadily assigned in these ‘Okay 2 ( pairwise classifications.
One-Versus-All Classifcation
The one-versus-all method (additionally known as one-versus-rest) is an al- one-versusall one-versusrest ternative process for making use of SVMs within the case of Okay > 2 lessons. We ft Okay SVMs, every time evaluating one of many Okay lessons to the remaining Okay − 1 lessons. Let β0k, β1k,…, βpk denote the parameters that outcome from ftting an SVM evaluating the kth class (coded as +1) to the others (coded as −1). Let x∗ denote a check commentary. We assign the commentary to the category for which β0k +β1kx∗ 1 +β2kx∗ 2 +···+βpkx∗ p is largest, as this quantities to a excessive stage of confdence that the check commentary belongs to the kth class moderately than to any of the opposite lessons
- Goal is to maximise the marginal distance between the marginal plans
- The marginal plan ought to go from a level which is closest to hyperplane. Factors are known as Help vector
- Goal of Kernal: Rework Low dimension to excessive dimension
- SVM Kernal — Polynomial, Sigmoid radial foundation operate
- Regularization — What number of error factors X Sum of distance of these error factors from plan
- Price operate in SVM is the hinge loss operate, which penalizes misclassifications. It goals to maximise the margin between the lessons whereas minimizing the classification errors.
- Hinge loss(y, f(x)) = max(0, 1 — y * f(x))
- If this isn’t larger than 1 then there’s a misclassification
- Simpler in excessive dimensional house as a result of that information is house and it is ready to get good assist vectors
- Over becoming is much less — To keep away from overfitting, we use Tender margins
- Extra coaching time, Tough to decide on good kernel, Tough to tune, Delicate to lacking worth and outlier
Essential Params —
- C — Regularization parament, it’s inversely proportional to Regularization power
- Kernal — Linear, ploy, rbf, sigmoid
- Gamma — Kernel coefficient for ‘rbf’, ‘poly’ and ‘sigmoid’. Increased values of gamma enable the mannequin to suit the coaching information extra exactly, probably resulting in overfitting.
- Coeff — Impartial time period in kernel operate. It’s only vital in ‘poly’ and ‘sigmoid’.
- Shrinkage — can velocity up the coaching, would possibly present inaccurate outcomes
- Likelihood — once we want likelihood estimate