How an Occasion-Sensible Price Perform Impacts SVC: Stating the Theorem
As we noticed, SVC can be utilized as a software to estimate the expressive energy of a speculation class inside a strategic classification context. Having rigorously outlined SVC as a generalization of the canonical VC dimension, we perceive that the 2 have a lot in widespread. When, although, does SVC diverge from its canonical counterpart? Can we provide you with a situation during which the strategic side of a classification drawback considerably will increase its complexity? It seems we will, with relative ease: linear classification.
Linear classification includes figuring out whether or not a knowledge level ought to be positively or negatively categorised based mostly on a linear perform utilized to its options. Geometrically, we will think about a linear classifier inducing a linear choice boundary in d-dimensional actual house (ℝᵈ ). Something on one facet of the boundary is positively categorised, and something on the opposite facet is negatively categorised. In a single-dimensional house, the choice boundary is a threshold (as we saw in the previous article). In two-dimensional house, it’s a line dividing the airplane. On the whole, it’s a hyperplane.
In canonical binary classification, the VC dimension of the speculation class comprising all linear classifiers in ℝᵈ is d + 1, which is finite. For instance, for d = 2 (linear classifiers in ℝ²), the VC dimension is 3. The Fundamental Theorem of Statistical Learning dictates that canonical linear classification is due to this fact PAC learnable.⁽¹⁾
Intuitively, we’d count on the identical conclusion to carry for the strategic analog of the issue. In any case, linear classifiers are a few of the easiest classifiers there are, and reasoning about them might be slightly pure.⁽²⁾
Nonetheless, that simplicity goes out the window as quickly as we throw instance-wise price features into the combo. As we are going to show:
Given a strategic linear classification drawback Sᴛʀᴀᴄ⟨H, R, c⟩, there exists an instance-wise price perform c(z; x) = ℓₓ(z – x) such that SVC(H, R, c) = ∞.
In different phrases, utilizing the Fundamental Theorem of Strategic Learning, we discover that linear classification in a strategic setting geared up with an instance-wise price perform isn’t typically PAC learnable. Apparently, it is not going to be PAC learnable even when we strip away as a lot complexity as we will. On this case, we are going to achieve this by specializing in strategic linear classification on the Cartesian airplane ( X ⊆ ℝ²) with the homogeneous choice class (R = { 1 }).
The extra basic conclusion will observe from the counterexample we are going to present below these simplifying circumstances. If strategic linear classification isn’t PAC learnable in ℝ², there is no such thing as a method it might be PAC learnable in any greater dimension. Likewise, each different choice class we specified by our setup is a strict generalization of the homogeneous choice class. If we might show PAC learnability for any of these choice lessons, we might additionally give you the option to take action for the less complicated case the place R = { 1 }.
From Labelings to Factors on the Unit Circle: Proof Setup
Primarily based on the assumptions above, we start by turning our consideration to the particular case Sᴛʀᴀᴄ⟨Hₗ, { 1 }, c⟩, with Hₗ being the speculation class comprising all linear classifiers in ℝ². We then initialize n two-dimensional function vectors on the origin: ∀ i ≤ n . xᵢ = (0, 0). Since we’re utilizing the homogeneous choice class, we now have that ∀ i ≤ n . rᵢ = 1. The one distinction between the info factors will probably be in how our price perform behaves on every of them. That is the place the crux of the proof lies, as we are going to quickly see.
Earlier than we talk about the associated fee perform at size, although, we have to geometrize the possible labelings of our unlabeled knowledge factors. As we noticed last time, a set of n unlabeled knowledge factors will need to have precisely 2ⁿ potential labelings. Representing a set of labelings (n-tuples) geometrically in ℝ² is comparatively easy: we merely choose an arbitrary level for every potential labeling. Specifically, we are going to select 2ⁿ such consultant factors on the unit circle, every assigned to a potential labeling. Whereas the actual coordinates of the consultant factors themselves are unimportant, we do require that every such level be distinctive. We additionally require that no two factors be origin-symmetric with respect to at least one one other.
We’ll denote this set of consultant factors by S. Having chosen our consultant factors, we use them to outline the origin-symmetric set S’, i.e., S’ = { (-x, –y) : (x, y) ∈ S }. Notice that S and S’ are disjoint (S ∩ S’ = ∅) as a consequence of how we chosen the factors in S.
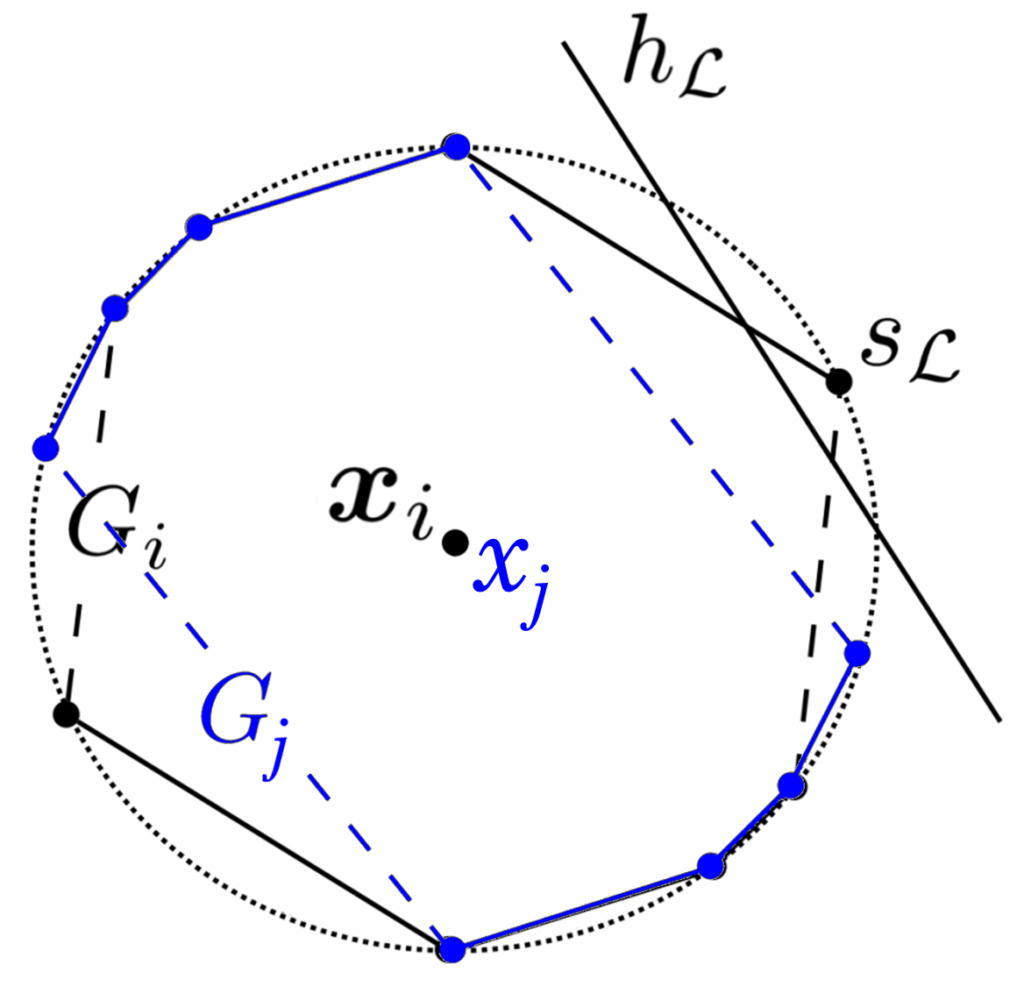
For a specific xᵢ, we outline Sᵢ because the subset of S that features solely the factors that signify labelings during which xᵢ is positively categorised. Equally, we derive the origin-symmetric Sᵢ’ ⊂ S’ from Sᵢ. Within the instance beneath, the factors above the x-axis are these representing labelings during which xᵢ is positively categorised, i.e., Sᵢ. These beneath the x-axis comprise their origin-symmetric set Sᵢ’ (with the numbering matching between symmetric pairs of factors). Notice that the number of factors above the x-axis is totally arbitrary.
We proceed to assemble a convex polygon Gᵢ, with its vertices being the factors in Sᵢ ∪ Sᵢ’. The Gᵢ for every unlabeled knowledge level will probably be key in designing an instance-wise price perform c with which we are going to at all times have the ability to obtain all potential labelings, thus exhibiting that SVC(Hₗ, { 1 }, c) = ∞. In direction of this finish, the convexity of Gᵢ will show important, as will its origin symmetry (stemming from our alternative of Sᵢ’ ).
Turning Polygons into Preferences: Developing the Price Perform
For every of the n origin-initialized, unlabeled knowledge factors we began with, we now have a convex, origin-symmetric polygon that represents the labelings during which it’s positively categorised. Every Gᵢ can now be used to outline the habits of our instance-wise price perform c on its corresponding xᵢ. We’ll use Gᵢ to outline a seminorm⁽³⁾:
∥ y ∥ɢᵢ = inf { ε ∈ ℝ⁺ : y ∈ εGᵢ }
This definition implies that the space between xᵢ and a few level z is lower than 1 if and provided that z lies inside Gᵢ. I.e.:
∥ z – xᵢ ∥ɢᵢ < 1 ⇔ z ∈ Gᵢ
For the remainder of the proof, it’s ample that we perceive this connection between ∥ ⋅ ∥ɢᵢ and a degree being inside Gᵢ. (See Footnote (3) for a dialogue of why ∥ ⋅ ∥ɢᵢ qualifies as a seminorm and for extra particulars about its geometric interpretation.)
We thus outline the instance-wise price perform c:
c(z; xᵢ) = ℓᵢ(z – xᵢ)
The place:
ℓᵢ(z – xᵢ) = ∥ z – xᵢ ∥ɢᵢ
That’s, for every unlabeled knowledge level xᵢ, c behaves as ∥ ⋅ ∥ɢᵢ would. Notice that this habits is completely different for every knowledge level. It’s because we constructed a novel Gᵢ for each xᵢ, and every ∥ ⋅ ∥ɢᵢ is derived from its corresponding polygon Gᵢ.
Information Level Greatest Response as a Results of the Price Perform
With the instance-wise price perform c in place, we could flip our consideration to how our knowledge factors work together with linear classifiers. Recall that we now have constrained our consideration to the homogeneous choice class, that means that r = 1 for all of our factors. I.e., xᵢ stands to achieve a reward of magnitude 1 for being positively categorised. Given a linear classifier, every knowledge level will thus be keen to incur any price lower than 1 to govern its function vector to make sure it falls on the constructive facet of the choice boundary. This may assure it receives constructive utility on account of the manipulation.
c is designed so {that a} knowledge level with function vector xᵢ has to pay ∥ z – xᵢ ∥ɢᵢ to vary its function vector to z. As we noticed, so long as z lies inside Gᵢ, this price will probably be lower than 1.
Suppose we now have a choice boundary that crosses Gᵢ (intersects it at two factors) with xᵢ falling on its damaging half-plane. As illustrated in Determine 3 beneath, this creates a sub-polygon such that for any z inside it:
- The fee to maneuver to z is lower than 1: c(z; xᵢ) = ∥ z — xᵢ ∥ɢᵢ < 1
- The realized reward for shifting is exactly 1: 𝕀(h(z) = 1) ⋅ r = 1
Whereby the utility for knowledge level i, 𝕀(h(z) = 1) ⋅ r – c(z; xᵢ), is constructive, in flip making any such z a greater response than non-manipulation. In different phrases, the info level will at all times need to manipulate its function vector into one which lies on this sub-polygon.
Conversely, given a choice boundary that does not cross Gᵢ, no such sub-polygon exists. The price of manipulating xᵢ to cross the boundary will at all times be better than 1, and thus not definitely worth the reward. The information level finest response would be the authentic function vector, that means it’s finest to remain put.
Isolating Consultant Factors Utilizing Linear Classifiers
We now perceive the strategic implications of whether or not or not a sure choice boundary crosses Gᵢ. Calling to thoughts the function of our factors on the unit circle as representatives of potential labelings, we will show the connection between labelings the place a knowledge level is positively categorised and linear classifiers.
Let 𝓛 be an arbitrary labeling of our n knowledge factors, and let sₗ ∈ S be its distinctive consultant level on the unit circle. Let xᵢ be considered one of our unlabeled knowledge factors. We’ll discover the habits of the info level with respect to a specific linear classifier, denoted hₗ. We require that the choice boundary induced by hₗ do the next:
- Cross the unit circle.
- Strictly separate sₗ from all different factors in S ∪ S’.
- Positively classify sₗ.
The construction of S ∪ S’ ensures that such an hₗ exists.⁽⁴⁾
With hₗ at our disposal, we could discover how our price perform c interacts with hₗ for xᵢ relying on whether or not or not xᵢ ought to be positively categorised below 𝓛. In truth, we are going to show {that a} knowledge level is positively categorised by hₗ if and solely whether it is positively labeled below 𝓛.
Allow us to first think about the case during which we wish xᵢ to be positively labeled (see Determine 5). Recall that we outlined Sᵢ as “the subset of S that features solely the factors that signify labelings during which xᵢ is positively categorised.” We all know, then, that sₗ ∈ Sᵢ. Specifically, sₗ should be one of many vertices of Gᵢ. The truth that hₗ strictly separates sₗ from all different factors in S ∪ S’ signifies that it’s strictly separated from the opposite vertices of Gᵢ. Therefore, hₗ should cross Gᵢ, incentivizing the info level to govern its function vector.
We proceed to look at the case during which we wish xᵢ to be negatively labeled below 𝓛 (see Determine 6). On account of how we constructed Sᵢ, sₗ ∉ Sᵢ. Moreover, having required that the origin-symmetric S’ be disjoint from S, we all know that sₗ ∉ Sᵢ’. It follows that sₗ isn’t a vertex of Gᵢ. As soon as once more, hₗ strictly separates sₗ from all different factors in S ∪ S’, together with all of the vertices of Gᵢ. As a result of Gᵢ is convex, we conclude that any level in Gᵢ is on the alternative facet of hₗ as sₗ. In different phrases, hₗ doesn’t cross Gᵢ. Consequently, the info level will select to remain put slightly than “overpaying” to govern its function vector to cross hₗ.
In abstract, our unlabeled knowledge level xᵢ will have interaction in manipulation to cross hₗ if and provided that 𝓛 dictates that the info level ought to be positively categorised. In our strategic classification setting, which means hₗ positively classifies a knowledge level if and provided that that knowledge level ought to be positively labeled in keeping with 𝓛.
Placing It All Collectively: Inducing an Arbitrary Labeling
Utilizing what we now have seen to date, we’re in a position to show that we will obtain any labeling of our n knowledge factors we wish. Overlaying all of our knowledge factors and their respective polygons (see Determine 7), we will see that given a labeling 𝓛, we’re in a position to obtain it with the assistance of a corresponding linear classifier hₗ.
Any knowledge level xᵢ that 𝓛 guidelines ought to be positively categorised will manipulate its function vector and transfer to the constructive facet of the choice boundary created by hₗ (just like the case in Determine 5). On the similar time, any knowledge level xⱼ that ought to be negatively categorised is not going to be sufficiently incentivized to govern its function vector, inflicting it to remain on the damaging facet of the choice boundary. Throughout all n knowledge factors, people who will probably be positively categorised will probably be precisely those that 𝓛 dictates ought to be positively categorised. In different phrases, we will induce any labeling we want.
We due to this fact have a pattern of n unlabeled, potentially-manipulated knowledge factors that’s strategically shattered by Hₗ, the speculation class of all linear classifiers in ℝ². Primarily based on how we defined strategic shattering coefficients, we discover that σₙ(Hₗ, { 1 }, c) = 2ⁿ. It follows that SVC(Hₗ, { 1 }, c) = ∞.