The abstract() technique within the statsmodels library is a handy solution to current the outcomes of a statistical mannequin in a tabular format. It gives complete particulars in regards to the mannequin match, coefficients, statistical exams, and goodness-of-fit measures.
Right here’s learn how to interpret the important thing sections of a abstract() output:
1. Mannequin Data
This part contains metadata in regards to the mannequin and dataset:
- Dependent Variable: The variable being predicted.
- Mannequin: The kind of mannequin used (e.g., OLS for Peculiar Least Squares).
- Methodology: The strategy used to estimate the parameters.
- Date: The date the mannequin was run.
- Time: The time the mannequin was run.
- Variety of Observations: The variety of information factors used.
- Df Residuals: Levels of freedom for residuals (n — okay — 1, the place okay is the variety of predictors).
- Df Mannequin: Levels of freedom for the mannequin (okay).
2. Goodness-of-Match Measures
These metrics consider how effectively the mannequin explains the information:
- R-squared: The proportion of variance within the dependent variable defined by the unbiased variables. Values vary from 0 to 1, with larger values indicating a greater match.
- Adjusted R-squared: A modified model of R-squared that adjusts for the variety of predictors. Helpful when evaluating fashions with totally different numbers of predictors.
- F-statistic and Prob (F-statistic): Assessments whether or not the general mannequin is statistically important. A low p-value (< 0.05) signifies the mannequin is critical.
- AIC (Akaike Data Criterion) and BIC (Bayesian Data Criterion): Metrics for mannequin choice; decrease values point out a greater mannequin, contemplating mannequin complexity.
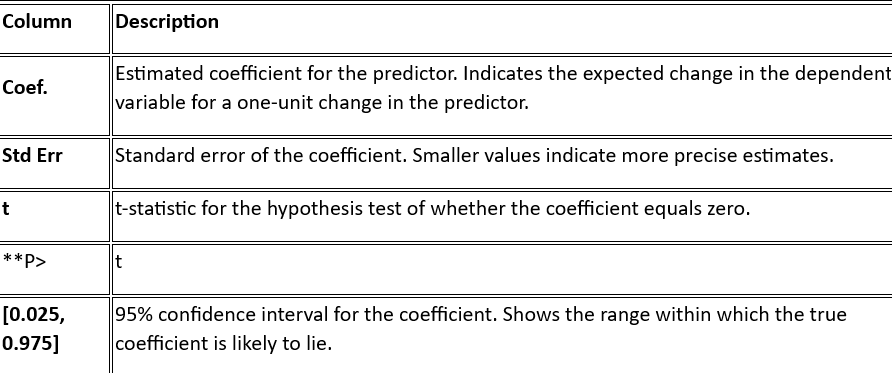
3. Coefficients Desk
That is the core of the output, displaying the estimated parameters for every unbiased variable:
4. Diagnostics (if out there)
- Durbin-Watson: Assessments for autocorrelation in residuals. Values near 2 point out no autocorrelation.
- Jarque-Bera (JB) and Prob(JB): Assessments whether or not the residuals are usually distributed.
- Skew: Measures the asymmetry of the residuals.
- Kurtosis: Measures the “tailedness” of the residuals.
- Situation Quantity: Signifies potential multicollinearity issues. Excessive values recommend multicollinearity.
Instance Output
Right here’s an instance of what the abstract() technique output would possibly appear like for an OLS regression:
How one can Learn This?
- The mannequin is statistically important (Prob (F-statistic) < 0.05).
- R-squared is 0.856, that means 85.6% of the variance within the dependent variable is defined by the predictors.
- The coefficient for X1 is 1.234, which is statistically important (p < 0.05). For each unit enhance in X1, the dependent variable will increase by 1.234.
- The coefficient for X2 is -0.456, which can be important. A unit enhance in X2 decreases the dependent variable by 0.456.
Within the supplied instance, the p-values are discovered within the column labeled P>|t| inside the coefficients desk. They point out the importance of every coefficient within the mannequin. Right here’s the related a part of the coefficients desk:
| Coefficient | Coef. | Std Err | t | P>|t| | [0.025, 0.975] | | — — — — — — -| — — — -| — — — — -| — — — -| — — — — — | — — — — — — — — | | Intercept | 2.546 | 0.512 | 4.970 | 0.000 | [1.516, 3.576] | | X1 | 1.234 | 0.123 | 10.049| 0.000 | [0.987, 1.481] | | X2 | -0.456| 0.201 | -2.268| 0.029 | [-0.861, -0.051] |
Key Factors on P-Values:
- Intercept: The p-value is 0.000. This means the intercept is statistically important.
- X1: The p-value is 0.000, displaying that the coefficient for X1 is very statistically important.
- X2: The p-value is 0.029, which is lower than 0.05. Thus, the coefficient for X2 can be statistically important however with much less confidence than X1.
How one can Interpret?
- A p-value lower than 0.05 (or your chosen significance degree) means that the corresponding variable has a statistically important impact on the dependent variable.
- On this case, each X1 and X2 have important coefficients, that means they’re probably vital predictors within the mannequin.