It could be excellent if the world of neural community represented a one-to-one relationship: every neuron prompts on one and just one function. In such a world, deciphering the mannequin can be simple: this neuron fires for the canine ear function, and that neuron fires for the wheel of automobiles. Sadly, that isn’t the case. In actuality, a mannequin with dimension d typically must characterize m options, the place d < m. That is once we observe the phenomenon of superposition.
Within the context of machine studying, superposition refers to a selected phenomenon that one neuron in a mannequin represents a number of overlapping options relatively than a single, distinct one. For instance, InceptionV1 accommodates one neuron that responds to cat faces, fronts of automobiles, and cat legs [1]. This results in what we are able to superposition of various options activation in the identical neuron or circuit.
The existence of superposition makes mannequin explainability difficult, particularly in deep studying fashions, the place neurons in hidden layers characterize complicated combos of patterns relatively than being related to easy, direct options.
On this weblog put up, we’ll current a easy toy instance of superposition, with detailed implementations by Python on this notebook.
We start this part by discussing the time period “function”.
In tabular information, there’s little ambiguity in defining what a function is. For instance, when predicting the standard of wine utilizing a tabular dataset, options could be the proportion of alcohol, the 12 months of manufacturing, and so forth.
Nonetheless, defining options can turn into complicated when coping with non-tabular information, corresponding to pictures or textual information. In these instances, there isn’t a universally agreed-upon definition of a function. Broadly, a function could be thought-about any property of the enter that’s recognizable to most people. For example, one function in a big language mannequin (LLM) could be whether or not a phrase is in French.
Superposition happens when the variety of options is greater than the mannequin dimensions. We declare that two crucial circumstances should be met if superposition would happen:
- Non-linearity: Neural networks sometimes embrace non-linear activation capabilities, corresponding to sigmoid or ReLU, on the finish of every hidden layer. These activation capabilities give the community prospects to map inputs to outputs in a non-linear approach, in order that it will probably seize extra complicated relationships between options. We will think about that with out non-linearity, the mannequin would behave as a easy linear transformation, the place options stay linearly separable, with none risk of compression of dimensions by superposition.
- Characteristic Sparsity: Characteristic sparsity means the truth that solely a small subset of options is non-zero. For instance, in language fashions, many options aren’t current on the similar time: e.g. one similar phrase can’t be is_French and is_other_languages. If all options have been dense, we are able to think about an essential interference on account of overlapping representations, making it very troublesome for the mannequin to decode options.
Artificial Dataset
Allow us to take into account a toy instance of 40 options with linearly reducing function significance: the primary function has an significance of 1, the final function has an significance of 0.1, and the significance of the remaining options is evenly spaced between these two values.
We then generate an artificial dataset with the next code:
def generate_sythentic_dataset(dim_sample, num_sapmple, sparsity):
"""Generate artificial dataset in line with sparsity"""
dataset=[]
for _ in vary(num_sapmple):
x = np.random.uniform(0, 1, n)
masks = np.random.selection([0, 1], measurement=n, p=[sparsity, 1 - sparsity])
x = x * masks # Apply sparsity
dataset.append(x)
return np.array(dataset)
This perform creates an artificial dataset with the given variety of dimensions, which is, 40 in our case. For every dimension, a random worth is generated from a uniform distribution in [0, 1]. The sparsity parameter, various between 0 and 1, controls the proportion of energetic options in every pattern. For instance, when the sparsity is 0.8, it the options in every pattern has 80% likelihood to be zero. The perform applies a masks matrix to understand the sparsity setting.
Linear and Relu Fashions
We’d now wish to discover how ReLU-based neural fashions result in superposition formation and the way sparsity values would change their behaviors.
We set our experiment within the following approach: we compress the options with 40 dimensions into the 5 dimensional house, then reconstruct the vector by reversing the method. Observing the conduct of those transformations, we anticipate to see how superposition types in every case.
To take action, we take into account two very comparable fashions:
- Linear Mannequin: A easy linear mannequin with solely 5 coefficients. Recall that we wish to work with 40 options — excess of the mannequin’s dimensions.
- ReLU Mannequin: A mannequin nearly the identical to the linear one, however with an extra ReLU activation perform on the finish, introducing one degree of non-linearity.
Each fashions are constructed utilizing PyTorch. For instance, we construct the ReLU mannequin with the next code:
class ReLUModel(nn.Module):
def __init__(self, n, m):
tremendous().__init__()
self.W = nn.Parameter(torch.randn(m, n) * np.sqrt(1 / n))
self.b = nn.Parameter(torch.zeros(n))def ahead(self, x):
h = torch.relu(torch.matmul(x, self.W.T)) # Add ReLU activation: x (batch, n) * W.T (n, m) -> h (batch, m)
x_reconstructed = torch.relu(torch.matmul(h, self.W) + self.b) # Reconstruction with ReLU
return x_reconstructed
In keeping with the code, the n-dimensional enter vector x is projected right into a lower-dimensional house by multiplying it with an m×n weight matrix. We then reconstruct the unique vector by mapping it again to the unique function house by a ReLU transformation, adjusted by a bias vector. The Linear Mannequin is given by the same construction, with the one distinction being that the reconstruction is finished through the use of solely the linear transformation as an alternative of ReLU. We prepare the mannequin by minimizing the imply squared error between the unique function samples and the reconstructed ones, weighted one the function significance.
We skilled each fashions with completely different sparsity values: 0.1, 0.5, and 0.9, from much less sparse to essentially the most sparse. Now we have noticed a number of essential outcomes.
First, regardless of the sparsity degree, ReLU fashions “compress” options a lot better than linear fashions: Whereas linear fashions primarily seize options with the very best function significance, ReLU fashions may concentrate on much less essential options by formation of superposition— the place a single mannequin dimension represents a number of options. Allow us to have a imaginative and prescient of this phenomenon within the following visualizations: for linear fashions, the biases are smallest for the highest 5 options, (in case you don’t bear in mind: the function significance is outlined as a linearly reducing perform primarily based on function order). In distinction, the biases for the ReLU mannequin don’t present this order and are typically lowered extra.
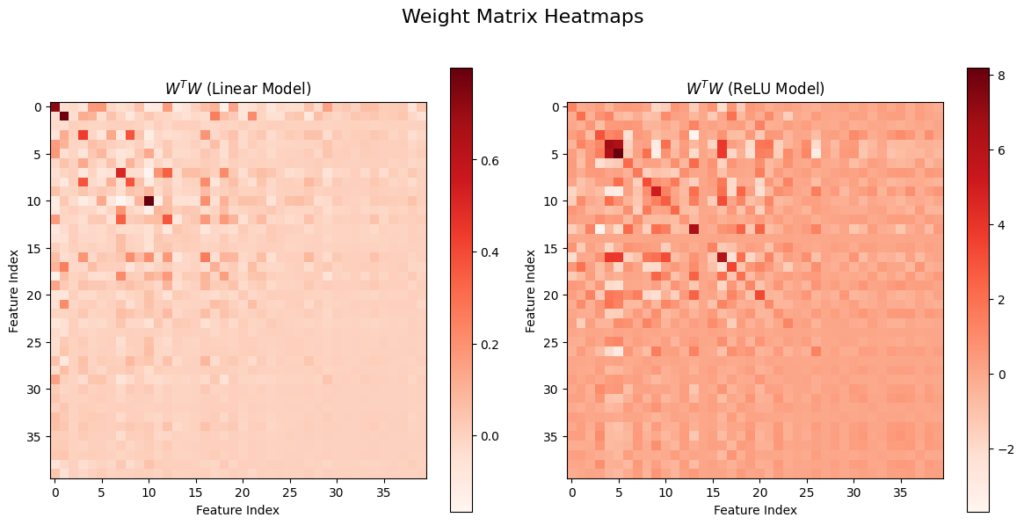
One other essential and fascinating result’s that: superposition is more likely to look at when sparsity degree is excessive within the options. To get an impression of this phenomenon, we are able to visualize the matrix W^T@W, the place W is the m×n weight matrix within the fashions. One may interpret the matrix W^T@W as a amount of how the enter options are projected onto the decrease dimensional house:
Particularly:
- The diagonal of W^T@W represents the “self-similarity” of every function contained in the low dimensional remodeled house.
- The off-diagonal of the matrix represents how completely different options correlate to one another.
We now visualize the values of W^T@W beneath for each the Linear and ReLU fashions we’ve constructed earlier than with two completely different sparsity ranges : 0.1 and 0.9. You may see that when the sparsity worth is excessive as 0.9, the off-diagonal components turn into a lot greater in comparison with the case when sparsity is 0.1 (You truly don’t see a lot distinction between the 2 fashions output). This remark signifies that correlations between completely different options are extra simply to be realized when sparsity is excessive.
On this weblog put up, I made a easy experiment to introduce the formation of superposition in neural networks by evaluating Linear and ReLU fashions with fewer dimensions than options to characterize. We noticed that the non-linearity launched by the ReLU activation, mixed with a sure degree of sparsity, can assist the mannequin kind superposition.
In real-world purposes, that are rather more complicated than my navie instance, superposition is a crucial mechanism for representing complicated relationships in neural fashions, particularly in imaginative and prescient fashions or LLMs.
[1] Zoom In: An Introduction to Circuits. https://distill.pub/2020/circuits/zoom-in/
[2] Toy fashions with superposition. https://transformer-circuits.pub/2022/toy_model/index.html