Electrical energy demand is without doubt one of the important indicators in sustaining the steadiness of the electrical energy system. Every day fluctuations influenced by climate, seasonal elements, and human actions make whole demand prediction a important problem in supporting extra environment friendly vitality planning and administration.
This venture implements numerous machine studying approaches to construct a complete vitality demand (MW) prediction mannequin based mostly on historic knowledge. Varied machine studying strategies are examined and their efficiency is objectively in comparison with determine probably the most correct mannequin in predicting whole demand based mostly on the traits of the out there knowledge.
Time
Time area represents attributes associated to time data.
Options on this area are essential to seize seasonality patterns or time developments that may have an effect on vitality demand variations.
Climate
temp2(c),temp2_max(c),temp2_min(c),temp2_ave(c): ambient temperature (in Celsius).suface_pressure: floor air stress (hectopascals / Pascals).wind_speed50_max(m/s): wind velocity at a peak of fifty meters.prectotcorr: that is more than likely the corrected precipitation whole (in mm or kg/m²).
Power
total_demand(mw): whole electrical energy demand in megawatts.max_generation: most whole electrical energy technology in megawatts.
df.data()
RangeIndex: 1362 entries, 0 to 1361
Knowledge columns (whole 16 columns):
# Column Non-Null Depend Dtype
--- ------ -------------- -----
0 date_1 1362 non-null object
1 day 1362 non-null int64
2 month 1362 non-null int64
3 12 months 1362 non-null int64
4 temp2(c) 1362 non-null float64
5 temp2_max(c) 1362 non-null float64
6 temp2_min(c) 1362 non-null float64
7 temp2_ave(c) 1362 non-null float64
8 suface_pressure(pa) 1362 non-null float64
9 wind_speed50_max(m/s) 1362 non-null float64
10 wind_speed50_min(m/s) 1362 non-null float64
11 wind_speed50_ave(m/s) 1362 non-null float64
12 prectotcorr 1362 non-null float64
13 total_demand(mw) 1343 non-null float64
14 date_2 1362 non-null object
15 max_generation(mw) 1339 non-null float64
dtypes: float64(11), int64(3), object(2)
reminiscence utilization: 170.4+ KBVariety of rows: 1362 entries (knowledge rows)
Variety of columns: 15 options
Knowledge kind:
int64as many as 3 columnsfloat64as many as 10 columnsobjectas many as 2 columns
There’s lacking worth in total_demand(mw) and max_generation
Checking Duplicate Knowledge, Lacking Values, and Distinctive
print("Knowledge duplicated:", df.duplicated().sum())# Mengecek jumlah NaN per kolom
print(df.isna().sum())
# Cek persentase lacking worth hanya di kolom tertentu
cols_to_check = ['total_demand(mw)', 'max_generation(mw)']
missing_percent = df[cols_to_check].isna().sum() / len(df) * 100
print(missing_percent)
Knowledge duplicated: 0
date_1 0
day 0
month 0
12 months 0
temp2(c) 0
temp2_max(c) 0
temp2_min(c) 0
temp2_ave(c) 0
suface_pressure(pa) 0
wind_speed50_max(m/s) 0
wind_speed50_min(m/s) 0
wind_speed50_ave(m/s) 0
prectotcorr 0
total_demand(mw) 19
date_2 0
max_generation(mw) 23
dtype: int64
total_demand(mw) 1.395007
max_generation(mw) 1.688693
dtype: float64
Deleting knowledge containing lacking values as a result of the quantity just isn’t too giant (<2%)
df = df.dropna()
df
print(df.isna().sum())
print("Distinctive Worth")
for col in df.columns:
print(f"{col}: {df[col].nunique()} distinctive values")
Distinctive Worth
date_1: 1328 distinctive values
day: 31 distinctive values
month: 12 distinctive values
12 months: 4 distinctive values
temp2(c): 764 distinctive values
temp2_max(c): 836 distinctive values
temp2_min(c): 790 distinctive values
temp2_ave(c): 972 distinctive values
suface_pressure(pa): 234 distinctive values
wind_speed50_max(m/s): 589 distinctive values
wind_speed50_min(m/s): 504 distinctive values
wind_speed50_ave(m/s): 798 distinctive values
prectotcorr: 704 distinctive values
total_demand(mw): 644 distinctive values
date_2: 1328 distinctive values
max_generation(mw): 1184 distinctive values
zero_counts = (df == 0).sum()
print(zero_counts)
date_1 0
day 0
month 0
12 months 0
temp2(c) 0
temp2_max(c) 0
temp2_min(c) 0
temp2_ave(c) 0
suface_pressure(pa) 0
wind_speed50_max(m/s) 0
wind_speed50_min(m/s) 0
wind_speed50_ave(m/s) 0
prectotcorr 427
total_demand(mw) 0
date_2 0
max_generation(mw) 0
dtype: int64
Within the prectotcorr characteristic, it nonetheless is smart if there’s a worth of 0, it could possibly be that the situation is certainly dry.
Boxplot visualization with IQR earlier than outlier dealing with
# Daftar kolom yang ingin divisualisasikan
kolom_2 = [
'day',
'month',
'year',
'temp2(c)',
'temp2_max(c)',
'temp2_min(c)',
'temp2_ave(c)',
'suface_pressure(pa)',
'wind_speed50_max(m/s)',
'wind_speed50_min(m/s)',
'wind_speed50_ave(m/s)',
'prectotcorr',
'total_demand(mw)',
'max_generation(mw)'
]# Membuat palet warna
color_palette = sns.color_palette("Set1", len(kolom_2))
plt.determine(figsize=(15, 10))
# Menghitung IQR untuk mendeteksi outliers
Q1 = df[kolom_2].quantile(0.25)
Q3 = df[kolom_2].quantile(0.75)
IQR = Q3 - Q1
# Menentukan batas bawah dan atas untuk outliers
lower_bound = Q1 - 1.5 * IQR
upper_bound = Q3 + 1.5 * IQR
# Record untuk menyimpan jumlah dan persentase outlier per kolom
outliers_counts = []
outliers_percent = []
# Loop untuk membuat boxplot
for i, column in enumerate(kolom_2, 1):
plt.subplot((len(kolom_2) + 2) // 3, 3, i) # Mengatur grid subplot secara lebih aman
sns.boxplot(knowledge=df, x=column, shade=color_palette[i - 1]) # Membuat boxplot per kolom
# Menentukan knowledge outliers
outliers = df[(df[column] < lower_bound[column]) |
(df[column] > upper_bound[column])]
# Menyimpan jumlah dan persentase outlier per kolom
outliers_counts.append(len(outliers))
outliers_percent.append(spherical(len(outliers) / len(df) * 100, 2))
plt.xlabel(column)
plt.title(f'{column} IQR Boxplot')
# Menyesuaikan structure agar tidak saling tumpang tindih
plt.tight_layout()
plt.present()
# Menampilkan jumlah dan persentase outliers dalam bentuk teks
for col, depend, pct in zip(kolom_2, outliers_counts, outliers_percent):
print(f'{col}: {depend} outliers ({pct}%)'
Dealing with Outlier
from scipy.stats.mstats import winsorize
import numpy as np
import pandas as pd# # Copy dataframe ke variabel baru
df_cleaned = df.copy()
# 1. Clip fitur dengan outlier < 1%
clip_cols = [
'temp2(c)',
'temp2_ave(c)',
'wind_speed50_min(m/s)',
'wind_speed50_ave(m/s)'
]
for col in clip_cols:
Q1 = df_cleaned[col].quantile(0.25)
Q3 = df_cleaned[col].quantile(0.75)
IQR = Q3 - Q1
decrease = Q1 - 1.5 * IQR
higher = Q3 + 1.5 * IQR
df_cleaned[col] = df_cleaned[col].clip(decrease, higher)
Clipping is chosen as a result of outliers in these options are comparatively minor and never too removed from the vary of affordable values. With clipping, we restrict excessive values which can be too excessive or too low however nonetheless retain a lot of the data from the info.
`temp2(c): Temperature can have regular fluctuations, however very low or very excessive is unrealistic.temp2_ave(c): Excessive each day temperature averages will be clipped to take care of a sensible temperature distribution.wind_speed50_min(m/s)andwind_speed50_ave(m/s): Wind speeds which can be too low or too excessive can have an effect on the evaluation outcomes, so they’re clipped to take care of knowledge stability.
from scipy.stats.mstats import winsorize# Melakukan winsorize pada kedua kolom secara terpisah
df_cleaned['temp2_max(c)'] = winsorize(df_cleaned['temp2_max(c)'], limits=[0.05, 0.05])
df_cleaned['wind_speed50_max(m/s)'] = winsorize(df_cleaned['wind_speed50_max(m/s)'], limits=[0.05, 0.05])
# Menampilkan statistik deskriptif sebelum dan sesudah winsorize
print("Earlier than:")
print(df[['temp2_max(c)', 'wind_speed50_max(m/s)']].describe())
print("nAfter:")
print(df_cleaned[['temp2_max(c)', 'wind_speed50_max(m/s)']].describe())
Earlier than:
temp2_max(c) wind_speed50_max(m/s)
depend 1328.000000 1328.000000
imply 30.185399 5.849149
std 4.073221 1.992202
min 17.800000 1.470000
25% 27.980000 4.440000
50% 30.800000 5.740000
75% 32.322500 7.000000
max 41.960000 21.300000After:
temp2_max(c) wind_speed50_max(m/s)
depend 1328.000000 1328.000000
imply 30.177944 5.780203
std 3.765384 1.670201
min 22.490000 3.120000
25% 27.980000 4.440000
50% 30.800000 5.740000
75% 32.322500 7.000000
max 37.080000 9.030000
Winsorizing is used for options which have important outliers that could be too removed from the conventional vary, however are nonetheless thought-about affordable within the context of the general knowledge. With winsorizing, we exchange the outliers with values which can be nearer to the higher or decrease limits of what’s affordable, with out utterly eradicating them.
temp2_max(c): Every day most temperatures will be fairly excessive, however some excessive values should be modified in order that they don’t have an effect on the mannequin.wind_speed50_max(m/s): Most wind velocity may also present excessive values, however extreme outliers might be trimmed to extra lifelike values.
df_cleaned['prectotcorr_log'] = np.log1p(df_cleaned['prectotcorr'])
The explanations for utilizing logarithmic transformation on prectotcorr are:
- Important Outliers: prectotcorr has many outliers (93 or 7%) that may considerably have an effect on the mannequin. Logarithmic transformation helps scale back the influence of those excessive values.
- Skewed Distribution: The prectotcorr knowledge tends to be skewed, so logarithmic transformation helps steadiness the distribution and make it extra regular.
- Mannequin Stability: By lowering excessive variations, logarithmic transformation makes the mannequin extra secure and simpler to study the principle patterns.
Boxplot visualization with IQR after outlier dealing with
- Excessive Temperature Correlation
The temperature values (temp2(c), temp2_max(c), temp2_min(c), temp2_ave(c)) are extremely correlated with one another, exhibiting practically good correlation (>0.90).
- Relationship Between Electrical energy Demand and Generator Capability
total_demand(mw) and max_generation(mw) have a correlation of 0.90. This implies that prime electrical energy demand is often adopted by a rise in technology capability.
- Rainfall Correlation and Its Transformation
prectotcorr and prectotcorr_log are strongly correlated (0.83). The log-transformed model (prectotcorr_log) is used because of its extra secure distribution, which is nearer to regular.
- Air Strain vs. Minimal Temperature
temp2_min(c) and suface_pressure(pa) present a powerful unfavourable correlation (-0.86). This means that greater air stress is usually related to decrease minimal temperatures, seemingly because of particular climate patterns.
- Redundancy in Wind Velocity Knowledge
Wind variables (wind_speed50_max, wind_speed50_min, wind_speed50_ave) are extremely correlated with one another (>0.90), suggesting redundancy within the knowledge.
Practice fitur with MinMaxScaler
practice = df_cleaned.copy()# Normalisasi fitur agar berada dalam rentang 0-1
scaler = MinMaxScaler()
scaled_data = scaler.fit_transform(practice.drop([
'date_1', 'date_2', 'prectotcorr', # Kolom temporal
'total_demand(mw)'# Kolom target
], axis=1))
y = practice['total_demand(mw)'].values
Lengthy Quick Time period Reminiscence
LSTM (Lengthy Quick-Time period Reminiscence) is used on this mannequin due to its primary potential to deal with time sequence knowledge, the place earlier values have an affect on future values. The information used exhibits seasonal patterns or time-dependent developments, making LSTM efficient in studying such temporal relationships. By utilizing time_steps = 10, this mannequin makes use of the earlier 10 occasions to foretell the long run worth of total_demand(mw), making it very related for data-based prediction functions like this.
The characteristic knowledge is normalized utilizing MinMaxScaler to be within the vary of 0–1. This course of is essential as a result of it helps the mannequin to work extra effectively with knowledge that has a constant scale. Normalization prevents options with a bigger vary of values from dominating the mannequin’s studying, whereas additionally dashing up the convergence of the coaching course of. After the info is normalized, train-test break up is used to divide the dataset into coaching and testing elements, guaranteeing that the mannequin will be evaluated correctly and avoiding overfitting on the coaching knowledge.
# Membuat dataset untuk LSTM dalam bentuk [samples, time steps, features]
def create_lstm_dataset(knowledge, goal, time_steps=1):
X, y = [], []
for i in vary(len(knowledge) - time_steps):
X.append(knowledge[i:(i + time_steps)])
y.append(goal[i + time_steps])
return np.array(X), np.array(y)time_steps = 10
X_lstm, y_lstm = create_lstm_dataset(scaled_data, y, time_steps)
# Practice-Check Cut up
X_train_lstm, X_test_lstm, y_train_lstm, y_test_lstm = train_test_split(X_lstm, y_lstm, test_size=0.2, random_state=42)
# Membangun mannequin LSTM
lstm_model = Sequential()
lstm_model.add(LSTM(items=50, return_sequences=False, input_shape=(X_train_lstm.form[1], X_train_lstm.form[2])))
lstm_model.add(Dense(items=1))
lstm_model.compile(optimizer='adam', loss='mean_squared_error')
# Melatih mannequin LSTM
lstm_model.match(X_train_lstm, y_train_lstm, epochs=10, batch_size=32, verbose=1)
# Prediksi dan Evaluasi
y_pred_lstm = lstm_model.predict(X_test_lstm)
mae_lstm = mean_absolute_error(y_test_lstm, y_pred_lstm)
print(f'Imply Absolute Error (LSTM): {mae_lstm}')
Imply Absolute Error (LSTM): 10108.685760461924
Practice fitur with out Scaler
# Persiapan Knowledge
practice = df_cleaned.copy()# Pisahkan Fitur dan Goal
X = practice.drop([
'date_1', 'date_2', 'prectotcorr', # Kolom temporal
'total_demand(mw)'# Kolom target
], axis=1)
y = practice['total_demand(mw)']
# Practice-Check Cut up
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Menyamakan urutan kolom antara X_train dan X_test
X_test = X_test[X_train.columns]
Random Forest
The Random Forest mannequin was chosen due to its potential to deal with knowledge with numerous kinds of options with out requiring a lot extra preprocessing. The options utilized in coaching have been chosen by eradicating temporal columns (date_1, date_2 ) and changing the prectotcorr variable with its extra secure transformation type. Random Forest is appropriate for software as a result of it is ready to seize advanced non-linear relationships between variables resembling temperature, wind velocity, air stress, and electrical energy manufacturing capability, which have dynamic dependence patterns on whole electrical energy demand total_demand(mw) . This mannequin makes use of an ensemble approach based mostly on many determination timber, thereby minimizing the chance of overfitting whereas rising the generalization of predictions on new knowledge.
# Practice Random Forest
rf_model = RandomForestRegressor(n_estimators=100, random_state=42)
rf_model.match(X_train, y_train)# Prediksi dan Evaluasi
y_pred_rf = rf_model.predict(X_test)
mae_rf = mean_absolute_error(y_test, y_pred_rf)
print(f'Imply Absolute Error (Random Forest): {mae_rf}')
print("R² Rating:", rf_model.rating(X_test, y_test))
Imply Absolute Error (Random Forest): 211.4306390977444
R² Rating: 0.9541438801905043
XGBoost
model_xgb = XGBRegressor(
n_estimators=200,
learning_rate=0.05,
random_state=42
)
model_xgb.match(X_train, y_train)# Evaluasi
y_pred_xgb = model_xgb.predict(X_test)
print("XGBoost Efficiency:")
print("XGBoost MAE:", mean_absolute_error(y_test, y_pred_xgb))
print("R² Rating:", model_xgb.rating(X_test, y_test))
XGBoost Efficiency:
XGBoost MAE: 229.0411349418468
R² Rating: 0.9299105962251898
Decission Tree
Choice Bushes are used as a result of they’re straightforward to interpret and might seize non-linear relationships in knowledge with out requiring particular pre-processing.
This mannequin divides the info based mostly on the circumstances that scale back probably the most impurities, so it may well instantly reveal essential patterns within the options of the dataset.
# Normalisasi (match di coaching, remodel di coaching & take a look at)
scaler = StandardScaler()
X_train_norm = scaler.fit_transform(X_train)
X_test_norm = scaler.remodel(X_test)# Choice Tree Regressor
tree = DecisionTreeRegressor(random_state=42)
tree.match(X_train_norm, y_train)
# Prediksi
y_pred = tree.predict(X_test_norm)
# Evaluasi
mae = mean_absolute_error(y_test, y_pred)
rmse = np.sqrt(mean_squared_error(y_test, y_pred))
r2 = r2_score(y_test, y_pred)
print("Choice Tree Regressor Efficiency:")
print(f"MAE: {mae:.2f}")
print(f"RMSE: {rmse:.2f}")
print(f"R² Rating: {r2:.2f}")
Choice Tree Regressor Efficiency:
MAE: 259.94
RMSE: 426.03
R² Rating: 0.92
Linear Regression
This mannequin assumes a linear relationship between options and targets, making it appropriate for measuring how huge a direct relationship there’s between enter variables and total_demand.
By attempting Linear Regression, it may be seen whether or not the connection sample within the knowledge is straightforward sufficient or requires a extra advanced mannequin.
model_lr = LinearRegression()
model_lr.match(X_train, y_train)# Evaluasi
y_pred_lr = model_lr.predict(X_test)
print("Linear Regression Efficiency")
print("Linear Regression MAE:", mean_absolute_error(y_test, y_pred_lr))
print("R² Rating:", model_lr.rating(X_test, y_test))
Linear Regression Efficiency
Linear Regression MAE: 317.28977801920007
R² Rating: 0.9241553777751903
Stacking Regressor: Ensemble of XGBoost, Linear Regression, and Random Forest
base_models = [
('xgb', XGBRegressor(n_estimators=200, learning_rate=0.05, random_state=42)),
('rf', RandomForestRegressor(n_estimators=100, random_state=42)),
('lr', LinearRegression())
]# Buat mannequin stacking
stack_model = StackingRegressor(
estimators=base_models,
final_estimator=LinearRegression()
)
# Latih mannequin stacking
stack_model.match(X_train, y_train)
# Simpan mannequin yang sudah dilatih
joblib.dump(stack_model, 'stacking_model.pkl')
# Evaluasi mannequin stacking
y_pred_stack = stack_model.predict(X_test)
print("Stacking MAE:", mean_absolute_error(y_test, y_pred_stack))
print("Stacking R² Rating:", stack_model.rating(X_test, y_test))
Stacking MAE: 210.68754271573795
Stacking R² Rating: 0.9542899856989027
Hyperparameter Tuning for Stacked Mannequin (XGBoost, Random Forest, and Linear Regression)
def goal(trial):
# Hyperparameter dari base fashions
xgb_n_estimators = trial.suggest_int("xgb_n_estimators", 50, 300)
xgb_learning_rate = trial.suggest_float("xgb_learning_rate", 0.01, 0.3)
rf_n_estimators = trial.suggest_int("rf_n_estimators", 50, 200)
rf_max_depth = trial.suggest_int("rf_max_depth", 3, 15)# Definisikan base fashions
base_models = [
('xgb', XGBRegressor(
n_estimators=xgb_n_estimators,
learning_rate=xgb_learning_rate,
random_state=42
)),
('rf', RandomForestRegressor(
n_estimators=rf_n_estimators,
max_depth=rf_max_depth,
random_state=42
)),
('lr', LinearRegression())
]
# Closing estimator bisa kamu ganti juga kalau mau
final_estimator = RidgeCV()
# Buat mannequin stacking
stack_model = StackingRegressor(
estimators=base_models,
final_estimator=final_estimator
)
# Coaching
stack_model.match(X_train, y_train)
# Prediksi dan hitung MAE
y_pred = stack_model.predict(X_test)
mae = mean_absolute_error(y_test, y_pred)
return mae # Tujuan: minimalkan MAE
# Jalankan Optuna Examine
examine = optuna.create_study(path="reduce")
examine.optimize(goal, n_trials=20)
# Ambil finest hyperparameters dari Optuna
best_params = examine.best_params
# Buat ulang base fashions dengan finest params
best_base_models = [
('xgb', XGBRegressor(
n_estimators=best_params['xgb_n_estimators'],
learning_rate=best_params['xgb_learning_rate'],
random_state=42
)),
('rf', RandomForestRegressor(
n_estimators=best_params['rf_n_estimators'],
max_depth=best_params['rf_max_depth'],
random_state=42
)),
('lr', LinearRegression())
]
# Closing estimator bisa diganti jika perlu
final_estimator = RidgeCV()
# Buat ulang mannequin stacking dengan parameter terbaik
best_stack_model = StackingRegressor(
estimators=best_base_models,
final_estimator=final_estimator
)
# Latih ulang mannequin
best_stack_model.match(X_train, y_train)
# Prediksi ulang
y_pred_best = best_stack_model.predict(X_test)
# Evaluasi
mae = mean_absolute_error(y_test, y_pred_best)
rmse = np.sqrt(mean_squared_error(y_test, y_pred_best)) # RMSE secara guide
r2 = r2_score(y_test, y_pred_best)
# Cetak hasil
print("Finest MAE:", mae)
print("Finest RMSE:", rmse)
print(f"R² Rating : {r2:.4f}")
print("Finest Hyperparameters:", best_params)
Finest MAE: 209.1082478920435
Finest RMSE: 331.4287166593046
R² Rating : 0.9538
Finest Hyperparameters: {'xgb_n_estimators': 261, 'xgb_learning_rate': 0.14408695908396266, 'rf_n_estimators': 125, 'rf_max_depth': 12}
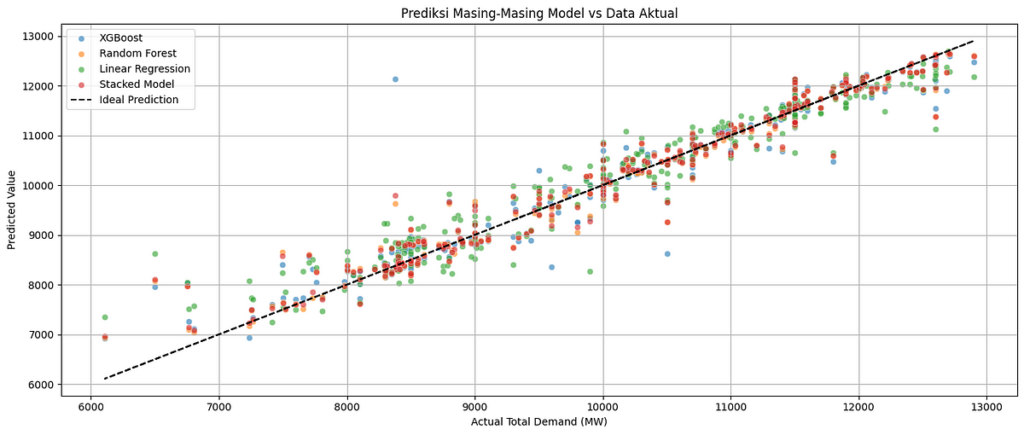
Based mostly on the accuracy outcomes of varied fashions, the one with good accuracy is the Stacking mannequin.
import pandas as pd
from xgboost import XGBRegressor
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_absolute_errortest_df = df_cleaned_test
X_test = test_df.drop([
'date_1', 'date_2', 'prectotcorr', # Kolom temporal
'total_demand(mw)'
], axis=1, errors='ignore')
stack_model = joblib.load('stacking_model.pkl')y_test_pred = stack_model.predict(X_test)
test_df['total_demand(mw)'] = y_test_pred
output_columns = ['date_1', 'total_demand(mw)']
test_df[output_columns].to_csv('predictions_results.csv', index=False)
pd.set_option('show.max_rows', None) # Tampilkan semua baris
print(test_df[['date_1', 'total_demand(mw)']].head(10))
submissions = pd.DataFrame({'date_1': test_df['date_1'], 'total_demand(mw)': y_test_pred})
submissions.to_csv('submission.csv', index=False)