are elementary objects in varied fields of recent laptop science and arithmetic, together with however not restricted to linear Algebra, machine studying, and laptop graphics.
Within the present collection of 4 tales, I’ll current a manner of decoding algebraic matrices in order that the bodily that means of assorted Matrix evaluation formulation will develop into clearer. For instance, the system for multiplying 2 matrices:
[begin{equation}
c_{i,j} = sum_{k=1}^{p} a_{i,k}*b_{k,j}
end{equation}]
or the system for inverting a series of matrices:
[begin{equation}
(ABC)^{-1} = C^{-1}B^{-1}A^{-1}
end{equation}]
In all probability for many of us, after we had been studying matrix-related definitions and formulation for the primary time, questions like the next ones arose:
- what does a matrix really signify,
- what’s the bodily that means of multiplying a matrix by a vector,
- why multiplication of two matrices is carried out by such a non-standard system,
- why for multiplication the variety of columns of the primary matrix should be equal to the variety of rows of the second,
- what’s the that means of transposing a matrix,
- why for sure varieties of matrices, inversion equals to transposition,
- … and so forth.
On this collection, I plan to current a technique of answering a lot of the listed questions. So let’s dive in!
However earlier than beginning, listed below are a few notation guidelines that I take advantage of all through this collection:
- Matrices are denoted by uppercase (like A, B), whereas vectors and scalars are denoted by lowercase (like x, y or m, n),
- ai,j – The worth of i-th row and j-th column of matrix ‘A‘,
- xi – the i-th worth of vector ‘x‘.
Multiplication of a matrix by a vector
Let’s put apart for now the only operations on matrices, that are addition and subtraction. The following easiest manipulation might be the multiplication of a matrix by a vector:
[begin{equation}
y = Ax
end{equation}]
We all know that the results of such an operation is one other vector ‘y‘, which has a size equal to the variety of rows of ‘A‘, whereas the size of ‘x‘ ought to be equal to the variety of columns of ‘A‘.
Let’s consider “n*n” sq. matrices for now (these with equal numbers of rows and columns). We’ll observe the habits of rectangular matrices a bit later.
The system for calculating yi is:
[begin{equation}
y_i = sum_{j=1}^{n} a_{i,j}*x_j
end{equation}]
… which, if written within the expanded manner, is:
[begin{equation}
begin{cases}
y_1 = a_{1,1}x_1 + a_{1,2}x_2 + dots + a_{1,n}x_n
y_2 = a_{2,1}x_1 + a_{2,2}x_2 + dots + a_{2,n}x_n
;;;;; vdots
y_n = a_{n,1}x_1 + a_{n,2}x_2 + dots + a_{n,n}x_n
end{cases}
end{equation}]
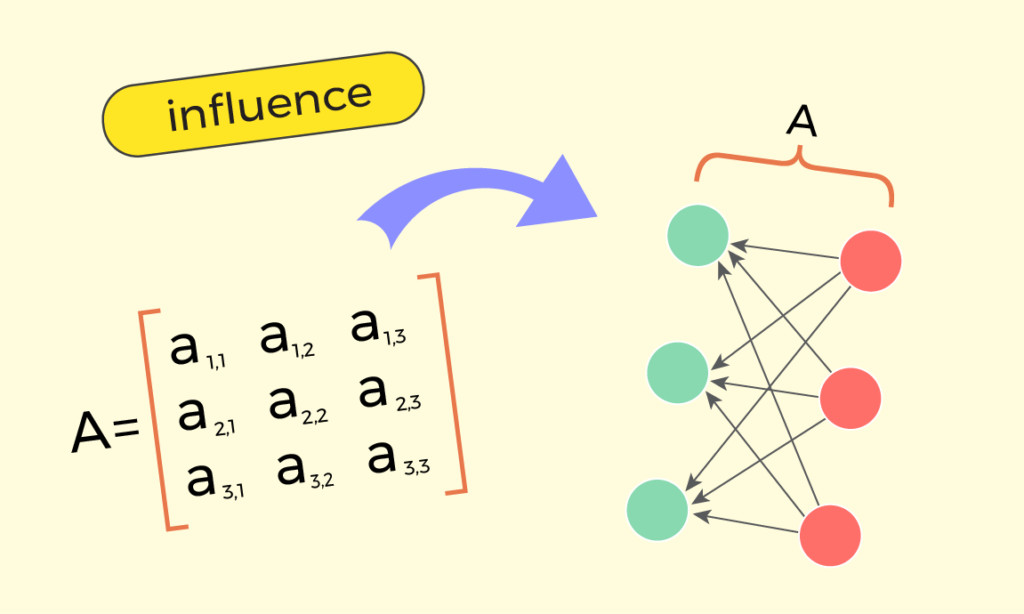
Such expanded notation clearly exhibits that each cell ai,j is current within the system of equations solely as soon as. Extra exactly, ai,j is current because the issue of xj, and participates solely within the sum of yi. This leads us to the next interpretation:
Within the product of a matrix by a vector “y = Ax”, a sure cell ai,j describes how a lot the output worth yi is affected by the enter worth xj.
Having that stated, we are able to draw the matrix geometrically, within the following manner:
And as we’re going to interpret matrix ‘A‘ as influences of values xj on values yi, it’s affordable to connect values of ‘x‘ to the best stack, which is able to end in values of ‘y‘ being current on the left stack.

I choose to name this interpretation of matrices as “X-way interpretation”, as the location of offered arrows appears to be like just like the English letter “X”. And for a sure matrix ‘A‘, I choose to name such a drawing as “X-diagram” of ‘A‘.
Such interpretation clearly exhibits that the enter vector ‘x‘ goes via some form of transformation, from proper to left, and turns into vector ‘y‘. That is the explanation why in Linear Algebra, matrices are additionally referred to as “transformation matrices”.
If any okay-th merchandise of the left stack, we are able to see how all of the values of ‘x‘ are being collected in the direction of it, whereas being multiplied by coefficients aokay,j (that are the okay-th row of the matrix).


On the similar time, if any okay-th merchandise of the best stack, we are able to see how the worth xokay is being distributed over all values of ‘y’, whereas being multiplied by coefficients ai,okay (which at the moment are the okay-th column of the matrix).


This already offers us one other perception, that when decoding a matrix within the X-way, the left stack will be related to rows of the matrix, whereas the best stack will be related to its columns.
Certainly, if we’re curious about finding some worth ai,j, its X-diagram will not be as handy as wanting on the matrix in its extraordinary manner – as an oblong desk of numbers. However, as we’ll see later and within the subsequent tales of this collection, X-way interpretation explicitly presents the that means of assorted algebraic operations over matrices.
Rectangular matrices
Multiplication of the shape “y = Ax” is allowed provided that the size of vector ‘x‘ is the same as the variety of columns of matrix ‘A‘. On the similar time, the consequence vector ‘y‘ can have a size equal to the variety of rows of ‘A‘. So, if ‘A‘ is an oblong matrix, vector ‘x‘ will change its size whereas passing via its transformation. We are able to observe it by X-way interpretation:


Now it’s clear why we are able to multiply ‘A‘ solely on such a vector ‘x‘, the size of which is the same as the variety of columns of ‘A‘: as a result of in any other case the vector ‘x‘ will merely not match on the best aspect of the X-diagram.
Equally, it’s clear why the size of the consequence vector “y = Ax” is the same as the variety of rows of ‘A‘.
Viewing rectangular matrices within the X-way strokes, now we have beforehand made an perception, which is that objects of the left stack of the X-diagram correspond to rows of the illustrated matrix, whereas objects of its proper stack correspond to columns.
Observing a number of particular matrices in X-way interpretation
Let’s see how X-way interpretation will assist us to know the habits of sure particular matrices:
Scale / diagonal matrix
A scale matrix is such a sq. matrix that has all cells of its most important diagonal equal to some worth ‘s‘, whereas having all different cells equal to 0. Multiplying a vector “x” by such a matrix ends in each worth of “x” being multiplied by ‘s‘:
[begin{equation*}
begin{pmatrix}
y_1 y_2 vdots y_{n-1} y_n
end{pmatrix}
=
begin{bmatrix}
s & 0 & dots & 0 & 0
0 & s & dots & 0 & 0
& & vdots
0 & 0 & dots & s & 0
0 & 0 & dots & 0 & s
end{bmatrix}
*
begin{pmatrix}
x_1 x_2 vdots x_{n-1} x_n
end{pmatrix}
=
begin{pmatrix}
s x_1 s x_2 vdots s x_{n-1} s x_n
end{pmatrix}
end{equation*}]
The X-way interpretation of a scale matrix exhibits its bodily that means. As the one non-zero cells listed below are those on the diagonal – ai,i, the X-diagram can have arrows solely between corresponding pairs of enter and output values, that are xi and yi.

A particular case of a scale matrix is the diagonal matrix (additionally referred to as an “identification matrix”), usually denoted with the letters “E” or “I” (we’ll use “E” within the present writing). It’s a scale matrix with the parameter “s=1″.
[begin{equation*}
begin{pmatrix}
y_1 y_2 vdots y_{n-1} y_n
end{pmatrix}
=
begin{bmatrix}
1 & 0 & dots & 0 & 0
0 & 1 & dots & 0 & 0
& & vdots
0 & 0 & dots & 1 & 0
0 & 0 & dots & 0 & 1
end{bmatrix}
*
begin{pmatrix}
x_1 x_2 vdots x_{n-1} x_n
end{pmatrix}
=
begin{pmatrix}
x_1 x_2 vdots x_{n-1} x_n
end{pmatrix}
end{equation*}]

We see that doing the multiplication “y = Ex” will simply go away the vector ‘x‘ unchanged, as each worth xi is simply multiplied by 1.
90° rotation matrix
A matrix, which rotates a given level (x1, x2) across the zero-point (0,0) by 90 levels counter-clockwise, has a easy kind:
[begin{equation*}
begin{pmatrix}
y_1 y_2
end{pmatrix}
=
begin{bmatrix}
0 & -1
1 & phantom{-}0
end{bmatrix}
*
begin{pmatrix}
x_1 x_2
end{pmatrix}
=
begin{pmatrix}
-x_2 phantom{-}x_1
end{pmatrix}
end{equation*}]

X-way interpretation of the 90° rotation matrix exhibits that habits:

Alternate matrix
An change matrix ‘J‘ is such a matrix that has 1s on its anti-diagonal, and has 0s in any respect different cells. Multiplying it by a vector ‘x‘ ends in reversing the order of values of ‘x‘:
[begin{equation*}
begin{pmatrix}
y_1 y_2 vdots y_{n-1} y_n
end{pmatrix}
=
begin{bmatrix}
0 & 0 & dots & 0 & 1
0 & 0 & dots & 1 & 0
& & vdots
0 & 1 & dots & 0 & 0
1 & 0 & dots & 0 & 0
end{bmatrix}
*
begin{pmatrix}
x_1 x_2 vdots x_{n-1} x_n
end{pmatrix}
=
begin{pmatrix}
x_n x_{n-1} vdots x_2 x_1
end{pmatrix}
end{equation*}]
This reality is explicitly proven within the X-way interpretation of the change matrix ‘J‘:

The 1s reside solely on the anti-diagonal right here, which signifies that output worth y1 is affected solely by enter worth xn, then y2 is affected solely by xn-1, and so forth, having yn affected solely by x1. That is seen on the X-diagram of the change matrix ‘J‘.
Shift matrix
A shift matrix is such a matrix that has 1s on some diagonal, parallel to the primary diagonal, and has 0s in any respect remaining cells:
[begin{equation*}
begin{pmatrix}
y_1 y_2 y_3 y_4 y_5
end{pmatrix}
=
begin{bmatrix}
0 & 1 & 0 & 0 & 0
0 & 0 & 1 & 0 & 0
0 & 0 & 0 & 1 & 0
0 & 0 & 0 & 0 & 1
0 & 0 & 0 & 0 & 0
end{bmatrix}
*
begin{pmatrix}
x_1 x_2 x_3 x_4 x_5
end{pmatrix}
=
begin{pmatrix}
x_2 x_3 x_4 x_5 0
end{pmatrix}
end{equation*}]
Multiplying such a matrix by a vector “x” ends in the identical vector however all values shifted by ‘okay‘ positions up or down. ‘okay‘ is the same as the space between the diagonal with 1s and the primary diagonal. Within the offered instance, now we have “okay=1″ (diagonal with 1s is just one place above the primary diagonal). If the diagonal with 1s is within the upper-right triangle, as it’s within the offered instance, then the shift of values of “x” is carried out upwards. In any other case, the shift of values is carried out downwards.
Shift matrix can be illustrated explicitly within the X-way:

Permutation matrix
A permutation matrix is a matrix composed of 0s and 1s, which rearranges all values of the enter vector “x” in a sure manner. The impression is that when multiplied by such a matrix, the values of “x” are being permuted.
To attain that, the n*n-sized permutation matrix ‘P‘ should have ‘n‘ 1s, whereas all different cells should be 0. Additionally, no two 1s should seem in the identical row or the identical column. An instance of a permutation matrix is:
[begin{equation*}
begin{pmatrix}
y_1 y_2 y_3 y_4 y_5
end{pmatrix}
=
begin{bmatrix}
0 & 0 & 0 & 1 & 0
1 & 0 & 0 & 0 & 0
0 & 0 & 0 & 0 & 1
0 & 0 & 1 & 0 & 0
0 & 1 & 0 & 0 & 0
end{bmatrix}
*
begin{pmatrix}
x_1 x_2 x_3 x_4 x_5
end{pmatrix}
=
begin{pmatrix}
x_4 x_1 x_5 x_3 x_2
end{pmatrix}
end{equation*}]
If drawing the X-diagram of the talked about permutation matrix ‘P‘, we’ll see the reason of such habits:

The constraint that no two 1s should seem in the identical column signifies that just one arrow ought to depart from any merchandise of the best stack. The constraint that no two 1s should seem on the similar row signifies that just one arrow should arrive at each merchandise of the left stack. Lastly, the constraint that every one the non-zero cells of a permutation matrix should be 1 signifies that a sure enter worth xj, whereas arriving at output worth yi, won’t be multiplied by any coefficient. All this ends in the values of vector “x” being rearranged in a sure method.
Triangular matrix
A triangular matrix is a matrix that has 0s in any respect cells both under or above its most important diagonal. Let’s observe upper-triangular matrices (the place 0s are under the primary diagonal), because the lower-triangular ones have related properties.
[
begin{equation*}
begin{pmatrix}
y_1 y_2 y_3 y_4
end{pmatrix}
=
begin{bmatrix}
a_{1,1} & a_{1,2} & a_{1,3} & a_{1,4}
0 & a_{2,2} & a_{2,3} & a_{2,4}
0 & 0 & a_{3,3} & a_{3,4}
0 & 0 & 0 & a_{4,4}
end{bmatrix}
*
begin{pmatrix}
x_1 x_2 x_3 x_4
end{pmatrix}
=
begin{pmatrix}
begin{aligned}
a_{1,1}x_1 + a_{1,2}x_2 + a_{1,3}x_3 + a_{1,4}x_4
a_{2,2}x_2 + a_{2,3}x_3 + a_{2,4}x_4
a_{3,3}x_3 + a_{3,4}x_4
a_{4,4}x_4
end{aligned}
end{pmatrix}
end{equation*}
]
Such an expanded notation illustrates that any output worth yi is affected solely by enter values with higher or equal indexes, that are xi, xi+1, xi+2, …, xN. If drawing the X-diagram of the talked about upper-triangular matrix, that reality turns into apparent:

Conclusion
Within the first story of the collection, which is dedicated to the interpretation of algebraic matrices, we checked out how matrices will be offered geometrically, and referred to as it “X-way interpretation”. Such interpretation explicitly highlights varied properties of matrix-vector multiplication, in addition to the habits of matrices of a number of particular varieties.
Within the subsequent story of this collection, we’ll discover an interpretation of the multiplication of two matrices by working on their X-diagrams, so keep tuned for the second arrival!
My gratitude to:
– Roza Galstyan, for cautious evaluation of the draft,
– Asya Papyan, for the exact design of all of the used illustrations ( https://www.behance.net/asyapapyan ).In the event you loved studying this story, be happy to attach with me on LinkedIn, the place, amongst different issues, I can even submit updates ( https://www.linkedin.com/in/tigran-hayrapetyan-cs/ ).
All used photographs, until in any other case famous, are designed by request of the writer.